24 Rings of Polynomials
We are used to thinking polynomials as an equation of a variable, say, ![]() . However, in this section, we will adopt a different viewpoint and an approach, and view polynomials in the context of a \textbf{ring}. To begin with, instead of referring
. However, in this section, we will adopt a different viewpoint and an approach, and view polynomials in the context of a \textbf{ring}. To begin with, instead of referring ![]() as a variable,
as a variable, ![]() will be called an \textbf{indeterminate}, and our goal will be shifted to “finding a zero or zeroes of a polynomial” from “solving a polynomial equation”. Let us begin with a formal definition of a polynomial ring.
will be called an \textbf{indeterminate}, and our goal will be shifted to “finding a zero or zeroes of a polynomial” from “solving a polynomial equation”. Let us begin with a formal definition of a polynomial ring.
Definition. For a ring ![]() , a polynomial
, a polynomial ![]() with coefficients
with coefficients ![]() is defined as an infinite formal sum as follows:
is defined as an infinite formal sum as follows:
![]()
where ![]() except for a finite number of
except for a finite number of ![]() ‘s.
‘s.
As usual, ![]() ‘s are the coefficients of
‘s are the coefficients of ![]() , and the largest value of
, and the largest value of ![]() such that
such that ![]() is the degree of
is the degree of ![]() .
.
We briefly introduce the underlying theory behind “solving a polynomial equation”, the evaluation homomorphisms for field theory [9]. Though seemingly trivial, in fact this is of crucial importance for the rest of our work.
Theorem. (Evaluation Homomorphisms for Field Theory)
Suppose ![]() , where
, where ![]() is a field, and let
is a field, and let ![]() .
.
Then, the map ![]() defined by
defined by
![]()
for ![]() is a homomorphism.
is a homomorphism.
Also, ![]() , and
, and ![]() for all
for all ![]() by
by ![]() .
.
Now, we can simply input, or substitute, our indeterminate ![]() with numbers of our interest. Owing to the evaluation homomorphisms for field theory, our journey of finding a zero of a polynomial has become finding
with numbers of our interest. Owing to the evaluation homomorphisms for field theory, our journey of finding a zero of a polynomial has become finding
![]()
such that
![]()
If we let ![]() and
and ![]() , the evaluation homomorphism for field theory turns into a common example found in elementary algebra.
, the evaluation homomorphism for field theory turns into a common example found in elementary algebra.
Factoring Over a Field
We begin with the division algorithm for ![]() [9] as this is the very basic tool of factorizing polynomials over a field.
[9] as this is the very basic tool of factorizing polynomials over a field.
Theorem. (Division Algorithm for ![]() )
)
Let ![]() with degrees
with degrees ![]() and
and ![]() , respectively, where
, respectively, where ![]() . Then, there exist unique polynomials
. Then, there exist unique polynomials ![]() and
and ![]() such that
such that
![]()
where ![]() or the degree of
or the degree of ![]() is smaller than
is smaller than ![]() .
.
Let us illustrate with an example [9].
Example. Find the factorization of a polynomial ![]() in
in ![]() .
.
Let ![]() .
.
Then, ![]() (mod 7).
(mod 7).
Therefore, ![]() is a factor of
is a factor of ![]() .
.
Therefore, ![]() .
.
Irreducible Polynomials
Not all polynomials can be factorized. Such polynomials are referred to as irreducible polynomials}, and formally defined [9] as:
Definition. (Irreducible Polynomials)
Let ![]() .
.
We say ![]() , a polynomial with the first or greater degree, is irreducible over
, a polynomial with the first or greater degree, is irreducible over ![]() or is an irreducible polynomial in
or is an irreducible polynomial in ![]() , if there does not exist
, if there does not exist ![]() and
and ![]() such that
such that
![]()
where the degrees of ![]() and
and ![]() are both lower than the degree of
are both lower than the degree of ![]() .
.
Note that a polynomial can be either reducible or irreducible depending on the context. For example, ![]() is reducible in
is reducible in ![]() as
as
![]()
yet is irreducible in ![]() , since
, since ![]() .
.
Let us illustrate with an example.
Example. Demonstrate the irreducibility of ![]() over
over ![]() .
.
We shall prove by contradiction, and as such, let us suppose the opposite, that ![]() is reducible over
is reducible over ![]() , where
, where ![]() .\\
.\\
Then, ![]() has either a zero, or is reduced to two quadratic polynomials.
has either a zero, or is reduced to two quadratic polynomials.
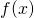 has a zero in
has a zero in 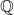 .
.
Then, by corollary 23.12[9], the zero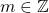 , and divides 1.
, and divides 1.
Then,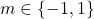 .
.
However,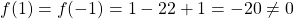 .
.
Therefore,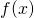 does not have a zero in
does not have a zero in  .
. is reduced to two quadratic polynomials.
is reduced to two quadratic polynomials.
Then, by theorem 23.11 [9], there exists![Rendered by QuickLaTeX.com g(x),h(x)\in \mathbb{Z}[x]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-38a445c21a1ba89a6e77d483ba2565ed_l3.png) such that
such that 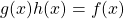 , where the order of
, where the order of 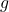 and
and 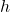 is 2.By letting
is 2.By letting 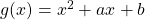 and
and 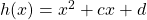 , and matching the coefficients of
, and matching the coefficients of 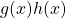 with
with 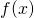 , there are two cases as follows:
, there are two cases as follows:
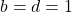
Then,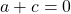 and
and 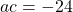 .
.
However, there does not exist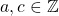 satisfying the equations above.
satisfying the equations above.
Therefore, there does not exist![Rendered by QuickLaTeX.com g(x),h(x)\in \mathbb{Z}[x]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-38a445c21a1ba89a6e77d483ba2565ed_l3.png) such that
such that 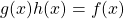 , where the order of
, where the order of 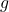 and
and 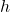 is 2.
is 2.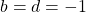
Then,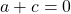 and
and 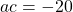 .
.
Again, there does not exist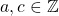 satisfying the equations above.
satisfying the equations above.
Therefore, there does not exist![Rendered by QuickLaTeX.com g(x),h(x)\in \mathbb{Z}[x]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-38a445c21a1ba89a6e77d483ba2565ed_l3.png) such that
such that 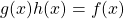 , where the order of
, where the order of 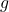 and
and 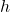 is 2.
is 2.
Therefore, ![]() neither has a zero nor is reducible to 2 quadratic polynomials.
neither has a zero nor is reducible to 2 quadratic polynomials.
This is a contradiction.
Therefore, ![]() is not irreducible over
is not irreducible over ![]() .
.
We conclude this section introducing the theorem about the uniqueness of factorization in ![]() [9]. While a full proof is not provided, the uniqueness should come intuitive to readers.
[9]. While a full proof is not provided, the uniqueness should come intuitive to readers.
Theorem. (Uniqueness of Factorization in ![]() )
)
When polynomials in ![]() are factorized until no more factorization is possible, the irreducible polynomials are unique except for order and non-zero constant factors.
are factorized until no more factorization is possible, the irreducible polynomials are unique except for order and non-zero constant factors.
