28 Eigenvalues and Eigenvectors
So far we have discussed the linear transformation ![]() , where
, where ![]() and
and ![]() . Now, we consider a special case
. Now, we consider a special case ![]() is mapped into a scalar multiple of itself, i.e. for scalar
is mapped into a scalar multiple of itself, i.e. for scalar ![]() ,
,
![]()
Naturally, ![]() is a
is a ![]() square matrix and it is a mapping from
square matrix and it is a mapping from ![]() onto itself for
onto itself for ![]() . To formally define relevant terms,
. To formally define relevant terms,
Definition. (Eigenvalue and Eigenvector)
Given a matrix equation ![]() , where
, where ![]() is a
is a ![]() matrix and
matrix and ![]() is a scalar,
is a scalar,
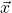 is an eigenvector of
is an eigenvector of  satisfying
satisfying
![Rendered by QuickLaTeX.com \[ A\vec{x}=\lambda\vec{x}\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-dc267cfe8eb87784f4b90475cccdb1fa_l3.png)
where
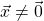 .
.- Such
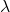 is called an eigenvalue.
is called an eigenvalue.
Note that the set of eigenvectors is in fact ![]() , where
, where ![]() . Therefore, this set, a subspace of
. Therefore, this set, a subspace of ![]() , is called the eigenspace of
, is called the eigenspace of ![]() corresponding to
corresponding to ![]() . Let us illustrate with an example.
. Let us illustrate with an example.
Example. Examine whether 3 is an eigenvalue of 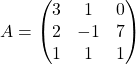 .
.
Let us find the ![]() by letting
by letting ![]() .
.
Then,
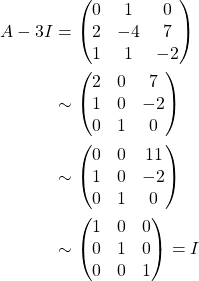
Therefore, ![]() is invertible and
is invertible and ![]() .
.
Therefore, 3 is not an eigenvalue of ![]() .
.
Characteristic Equation
We saw, for non-trivial solutions of ![]() to exist,
to exist, ![]() has to be singular, i.e not invertible. That is,
has to be singular, i.e not invertible. That is,
![]()
We call this a characteristic equation of ![]() . And by solving this characteristic equation, we can efficiently identify eigenvalues.
. And by solving this characteristic equation, we can efficiently identify eigenvalues.
Diagonalization
Now we turn our attention to decomposition of a matrix, factorizing into multiple matrices. Suppose we want to compute ![]() , the
, the ![]() -th power of a
-th power of a ![]() matrix
matrix ![]() , where the value of
, where the value of ![]() is large. Then, it would be a computationally expensive task to do it straightforward. However, if it is the case a given matrix can be decomposed, this cumbersome task can be substantially lightened. In this section, we introduce a special case of decomposition or factorization of a matrix called diagonalization.
is large. Then, it would be a computationally expensive task to do it straightforward. However, if it is the case a given matrix can be decomposed, this cumbersome task can be substantially lightened. In this section, we introduce a special case of decomposition or factorization of a matrix called diagonalization.
Definition. (Diagonalization)
A ![]() matrix
matrix ![]() is diagonalizable if there exists an invertible matrix
is diagonalizable if there exists an invertible matrix ![]() and a diagonal matrix
and a diagonal matrix ![]() such that
such that
![]()
Note how easy and lightweighted the involved computation of the ![]() -th power of
-th power of ![]() becomes when
becomes when ![]() is diagonalizable as
is diagonalizable as ![]() .
.
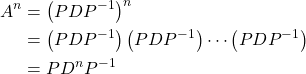
Let us illustrate with an example.
Example. Compute ![]() of a diagonalizable matrix
of a diagonalizable matrix 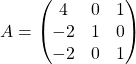 , whose eigenvalues are
, whose eigenvalues are ![]() .
.
1. Let us first find the eigenvectors of ![]() , where non-trivial solutions of
, where non-trivial solutions of ![]() .
.
(a) 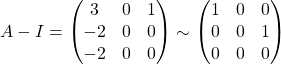 .
.
Therefore, 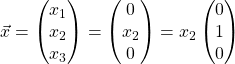 , for
, for ![]() .
.
(b) 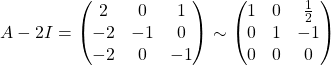 .\\
.\\
Therefore, 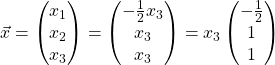 , for
, for ![]() .
.
(c) 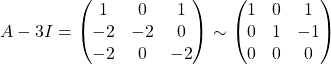 .\\
.\\
Therefore, 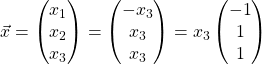 , for
, for ![]() .
.
2. Construct 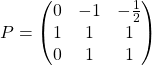 from linearly independent eigenvectors identified above, where the order is irrelevant.
from linearly independent eigenvectors identified above, where the order is irrelevant.
Then, identify ![]() .
.
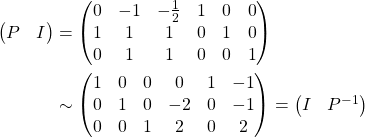
Therefore, 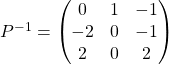 .
.
3. Construct 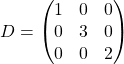 so that the order of eigenvalues matches the order
so that the order of eigenvalues matches the order ![]() was constructed.
was constructed.
4. Compute ![]()
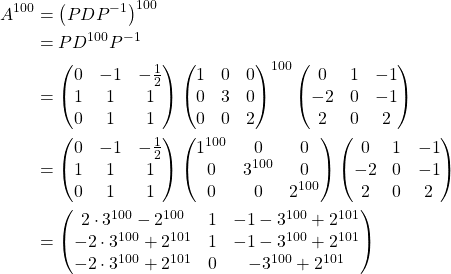
Therefore,
![Rendered by QuickLaTeX.com \[ A^{100} = \begin{pmatrix} 2\cdot 3^{100}-2^{100} & 1 & -1-3^{100}+2^{101}\\ -2\cdot 3^{100}+2^{101} & 1 & -1-3^{100}+2^{101}\\ -2\cdot 3^{100}+2^{101} & 0 & -3^{100}+2^{101} \end{pmatrix}\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8df845dddcadef496e6475fd81950141_l3.png)
Note that the computation of ![]() of a diagonalizable matrix
of a diagonalizable matrix ![]() is substantially simplified by the property of a diagonal matrix
is substantially simplified by the property of a diagonal matrix ![]() :
:
![Rendered by QuickLaTeX.com \[ D^n = \begin{pmatrix} d_1 &0 &\cdots &0\\ 0 &d_2 &\cdots &\vdots\\ \vdots &\cdots &\ddots &0\\ 0 &\cdots &0 &d_n\\ \end{pmatrix}^n = \begin{pmatrix} d_1^n &0 &\cdots &0\\ 0 &d_2^n &\cdots &\vdots\\ \vdots &\cdots &\ddots &0\\ 0 &\cdots &0 &d_n^n\\ \end{pmatrix}\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a67b724adc86ccfa8ca73b0555f319a5_l3.png)
