4 Applications
As aforementioned at the very beginning, the area where calculus is applied is almost universal in scientific domain – natural sciences, social sciences such as economics and politics, any situation linking the rate of change with a total change with mathematical modeling, and so on.
In this section, application in physics, specifically in classical mechanics, and probability is introduced, as these two areas are specific domain the author has particular interest in.
Work in Physics
Work in physics is in fact equivalent to energy. One way of understanding work is the energy transferred from one system to another system, as the total amount of energy is preserved, following the first law of thermodynamics, the law of conservation of energy.
Suppose a situation where you apply force to lift an object against gravity. Then, you have worked in terms of physics, and as a result of your work the (gravitational) potential energy of the object has been increased by the same amount. Work is calculated as a product of force (![]() ) and distance (
) and distance (![]() ), i.e.
), i.e.
![]()
Note here work is a product, a multiplication of force and distance. Then, what if the force applied during the course of action varies? The solution is, then,
![]()
Let us clarify this with an example.
Example. A 200 kg cable is 10 m long and hangs vertically from the top of a tall building. How much work is required to lift the cable to the top of the building? The gravitational acceleration is ![]() .
.
Let us project the cable to the hypothetical coordinate, where the origin is at the bottom of the building and the ![]() -axis point upwards. Then, think of the cable divided into small pieces with length
-axis point upwards. Then, think of the cable divided into small pieces with length ![]() . In fact,
. In fact, ![]() represents each point on the cable, and each
represents each point on the cable, and each ![]() is lifted by
is lifted by ![]() m.
m.
The cable weighs ![]() . Therefore,
. Therefore,
![Rendered by QuickLaTeX.com \begin{align*} W &= \int F\, dx\\ &= \int_{0}^{10} \left(20\,dy \right) (10-y)\\ &= 200\int_{0}^{10} (10-y)\,dy\\ &= 200\left[ 10y-\frac{1}{2}y^2\right]_{0}^{10}\\ &= 10000\, \left[ J=N\cdot m\right] \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f7f88948ec47658743393a6e75a599ef_l3.png)
Therefore, 10,000 ![]() of work is required to lift the cable to the top of the building.
of work is required to lift the cable to the top of the building.
Here is another example.
Example. Hooke’s law states the force needed to stretch or compress a spring from a natural state is proportional to displacement (![]() ), i.e.
), i.e. ![]() . Evaluate the work applied to the spring when the spring is extended by 5 cm whose spring constant is
. Evaluate the work applied to the spring when the spring is extended by 5 cm whose spring constant is ![]() .
.
First, let us convert the extended distance into meter, 5 cm = 0.05 m, since the spring constant is in ![]() . Therefore,
. Therefore,
![Rendered by QuickLaTeX.com \begin{align*} \int _{0}^{0.05} kx \, dx &= \int _{0}^{0.05} 100x \, dx\\ &= \left[ 50x^2\right]_{0}^{0.05}\\ &= 50\left(\left( 0.05\right)^2-0^2\right)\\ &= 0.125 \, \left[ J=N\cdot m\right] \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-53e534653e7320bdf80caa6b1a45f9d1_l3.png)
Therefore, we conclude 0.125 ![]() of work is required, or the same amount of \textbf{potential energy} is saved, by the extension of the spring by 5 cm.
of work is required, or the same amount of \textbf{potential energy} is saved, by the extension of the spring by 5 cm.
Probability
Calculus also plays a crucial role in the analysis of random behavior, specifically of continuous random variables. In probability theory, a \textbf{probability density function (PDF)} ![]() is defined for a continuous random variable
is defined for a continuous random variable ![]() , with the following properties:
, with the following properties:
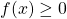 for all
for all 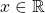
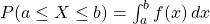
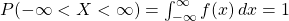
Let us explore some traits with examples.
Example. Let ![]() for
for ![]() , and
, and ![]() for
for ![]() . Find a constant
. Find a constant ![]() such that
such that ![]() be a probability density function.
be a probability density function.
1. ![]() for all
for all ![]()
- When
![Rendered by QuickLaTeX.com x \in [0,10]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3377a5c55d0ee160c152281d3601a1a3_l3.png) , then
, then 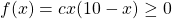
Therefore,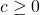 , since
, since 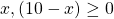
- When
![Rendered by QuickLaTeX.com x \in \mathbb{R} - [0,10]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a16e6fc73861cf2e3988f06d4b2553c0_l3.png) , then
, then 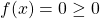
2. ![]()
![Rendered by QuickLaTeX.com \begin{align*} \int _{-\infty}^{\infty} f(x)\,dx &= \int _{-\infty}^{0} f(x)\,dx +\int _{0}^{10} f(x)\,dx + \int _{10}^{\infty} f(x)\,dx\\ &= \int _{-\infty}^{0} 0\,dx +\int _{0}^{10} cx(10-x)\,dx + \int _{10}^{\infty} 0\,dx\\ &= 0 + c\int _{0}^{10} (10x-x^2)\,dx + 0\\ &= c \left[ 5x^2-\frac{1}{3}x^3\right]_{0}^{10}\\ &= c \left( 500- \frac{1000}{3}\right)\\ &= 1 \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b19e007efa685e7368a515a3c2e73bef_l3.png)
Therefore, ![]() .
.
Following is another example.
Example. The mean or average ![]() of any probability density function
of any probability density function ![]() is defined as
is defined as
![]()
Find the mean of the probability density function ![]() defined by
defined by ![]() for
for ![]() and else
and else ![]() .
.
![Rendered by QuickLaTeX.com \begin{align*} \mu &= \int _{-\infty}^{\infty} xf(x)\,dx\\ &= \int _{-\infty}^{0} xf(x)\,dx + \int _{0}^{\infty} xf(x)\,dx\\ &= \int _{-\infty}^{0} 0\,dx + \int _{0}^{\infty} cxe^{-cx}\,dx\\ &= \int _{0}^{\infty} cxe^{-cx}\,dx\\ &= \lim_{t \to \infty} \int _{0}^{t} cxe^{-cx}\,dx\\ &= \lim_{t \to \infty} \left( -xe^{-cx}\vert_{0}^{t} + \int _{0}^{t} e^{-cx}\,dx \right)\\ &= \lim_{t \to \infty} \left( -te^{-ct} + \left[ -\frac{1}{c}e^{-cx}\right]_{0}^{t}\right)\\ &= \lim_{t \to \infty} \left( -te^{-ct} -\frac{1}{c}e^{-ct} +\frac{1}{c}\right)\\ &= \frac{1}{c} \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-58c2517bb107b7cb71427bf3d9bad56a_l3.png)
Therefore, the average is ![]() .
.
