17 Axioms of the Real Numbers
The set of real numbers can be described as a “complete ordered field” [12]. In this section and in the following, we shall discuss
- What a field is
- What an ordered field is
- What completeness is, and thus what a complete ordered field is
To begin with, we first need to define a field.
Definition. (Field)
A field is a commutative division ring. [9]
However, we have not introduced what a ring is. Therefore, we formally define a ring as follows:
Definition. (Ring)
A ring ![]() is a set
is a set ![]() , on which two binary operations, addition
, on which two binary operations, addition ![]() and multiplication
and multiplication ![]() , are defined, with the following properties:
, are defined, with the following properties:
1. For all ![]() ,
,
(a) Closure
![]()
(b)Associativity
![]()
(c) The existence of an identity element
![]() such that
such that ![]()
![]() such that
such that ![]()
(d) The existence of an inverse
![]() such that
such that ![]()
![]() such that
such that ![]() , except when
, except when ![]()
2. Addition ![]() is commutative, i.e.
is commutative, i.e. ![]()
3. The left and right distributive law holds, i.e.
![]()
Therefore, a field, a commutative division ring, refers to a ring, where multiplication ![]() is also commutative.
is also commutative.
Now we turn our focus to orderedness. To begin with, let us formally define well-ordering.
Definition. (Well-Ordering Property of ![]() )
)
Let ![]() . Then, there exists
. Then, there exists ![]() such that
such that ![]() for all
for all ![]() .
.
In other words, this can be restated as every nonempty subset of ![]() has a smallest element. Also, note that this well-ordering property is in fact equivalent to the principles of mathematical induction. That is, one implies the other, and vice versa.
has a smallest element. Also, note that this well-ordering property is in fact equivalent to the principles of mathematical induction. That is, one implies the other, and vice versa.
Let us illustrate with an example.
Example. Show that ![]() defined by
defined by ![]() is not an ordered field.
is not an ordered field.
Let us first examine whether ![]() is a field.
is a field.
In fact, showing one counterexample for any of the axioms that have to be satisfied for ![]() to be a field would suffice to prove
to be a field would suffice to prove ![]() is not a field.
is not a field.
Such counterexample is ![]() .
.
![]()
One of important properties of a field, of any binary operation, is a closure property, and we can see ![]() is not closed under multiplication.
is not closed under multiplication.
Therefore, ![]() is not a field.
is not a field.
For a field to become an ordered field, we need 4 more conditions or axioms as follows:
Let us define a relation “![]() ” on
” on ![]() . Then, for all
. Then, for all ![]() ,
,
- Trichotomy Law. It is only one of the cases
![Rendered by QuickLaTeX.com \[ x=y,x>y,\text{ or }x<y\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d6a14c787b0385a2158d0be6697f391d_l3.png)
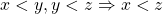
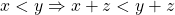
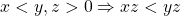
In fact, based on the 4 axioms mentioned above, we can reach a few useful theorems as follows:
Theorem.
For ![]() ,
,
![]()
![]()
Proof.
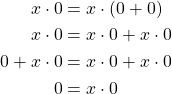
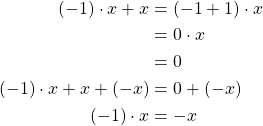
Now, let us have a look at how the absolute value is defined.
Definition. (Absolute Value)
The absolute value ![]() of
of ![]() is defined as
is defined as
![Rendered by QuickLaTeX.com \[ |x|= \begin{cases} x, &\text{if } x \geq 0 \\ -x, &\text{if } x<0 \end{cases} \]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e517e327af8200d989b3ef64ff0934f6_l3.png)
Again, a few useful theorems can be yielded as follows:
Theorem.
For ![]() and
and ![]()
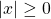
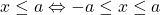
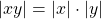
- Triangle Inequality
![Rendered by QuickLaTeX.com \[ |x+y| \leq |x|+|y|\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8ce696496989a160a937064a5700bb64_l3.png)
Reflecting the importance and utility of triangle inequality, the proof is provided here.
Proof. (Triangle Inequality)
By definition,
![]()
By summation, we obtain
![]()
Therefore,
![]()
Let us utilize the triangle inequality in an example.
Example. Prove ![]() for all
for all ![]() .
.
By triangle inequality,
![]()
Therefore,
![]()
Likewise,
![]()
In fact,
![]()
Therefore,
![]()
Therefore,
![]()
