Cardinality

Donovan D Chang

15 Cardinality

Let us recall our path so far. First, we studied sets and the set theory. Then, we related elements within the set itself, as well as across multiple sets. Then, we advanced our thoughts on relations to functions. However, we have been missing a concept of crucial importance so far – cardinality. In plain terms, cardinality refers to the number of elements of a given set. That being said, we might as well wonder, for example, should it not be the case the number of elements has to be the same for a bijection, and also for an inverse function, to be defined?

Let us begin with the definition of the equivalence of sets.

Finite Sets

Definition.
The sets $A$ and $B$ are equivalent, denoted

$A\approx B$

if there exists a bijection from $A$ to $B$ .

Naturally, it follows that

Theorem.
The equivalence of sets is an equivalence relation.

Viewing the cardinality as the number of elements in a given set, it is intuitive the equivalence of sets is indeed an equivalence relation. Let us formally define cardinality.

Definition. (Finite and Infinite Sets)
Let $\mathbb{N}_k = \left\lbrace 1,2,3,\cdots,k\right\rbrace$ for $k\in \mathbb{N}$ . Then, a set $S$ is
* finite, if $S=\emptyset$ or there exists $\mathbb{N}_k$ such that $S\approx \mathbb{N}_k$
* infinite, otherwise.

Definition. (Cardinality)
The cardinality or the cardinal number of a finite set $S$ is defined as the number $k\in \mathbb{N}$ such that
$S\approx\mathbb{N}_k$ and denoted $|S|=k$

In case $S=\emptyset$ , then $|S|=0$ .

A useful theorem that overlaps with the set theory is introduced as follows:

Theorem.
For finite sets $A$ and $B$ , $A \cup B$ is finite and

$\left\vert A\cup B\right\vert = |A|+|B|-\left\vert A\cap B\right\vert$

Here we introduce another theorem known as the Pigeonhole Principle. In colloquial terms, suppose there are $n$ pigeon holes, while there are $r$ pigeons. If the number of holes and pigeons are not the same, then naturally there would be extra, either holes or pigeons. Formally,

Theorem. (The Pigeonhole Principle)
For $f:\mathbb{N}_n\rightarrow \mathbb{N}_r$ , where $n,r\in \mathbb{N}$ ,
If $n>r$ , then $f$ is not bijective.

Proof.
Our proof utilizes the principles of mathematical induction (PMI), with the proof by contradiction. Since $n>r\geq 1$ , we begin with $n=2$ setting the statement of pigeon hole principle as $P(n)$ .

1. (Basis Step)
When $n=2$ , then $r=1$ , for $n,r\in \mathbb{N}$ .
Therefore, $f$ is not bijective.

2. (Inductive Step)
Suppose the pigeonhole principle is true for $n\in \mathbb{N} \setminus \left\lbrace 2\right\rbrace$ .
Then, there is no bijection $f:\mathbb{N}_n\rightarrow \mathbb{N}_r$ .

Now, let us suppose the negation of $P(n+1)$ , i.e. there exists a bijection $f:\mathbb{N}_{n+1}\rightarrow \mathbb{N}_r$ where $n+1>r \geq 1$ .
Then,

$\left\vert\mathbb{N}_{n+1}\right\vert = n+1 = r = \left\vert\mathbb{N}_r\right\vert$

This is contradiction, since $n+1>r$ .
Therefore, it must be the case our supposition is false, i.e. there does not exist a bijection $f:\mathbb{N}_{n+1}\rightarrow \mathbb{N}_r$ where $n+1>r \geq 1$ .

3. Therefore, we conclude $P(n)$ is true for all $n\in \mathbb{N} \setminus \left\lbrace 2\right\rbrace$ by the principles of mathematical induction.

In fact, the pigeonhole principle is simply another way of stating the non-equivalence of sets.

Infinite Sets

Now we delve into infinite sets. Recall the definition of infinite sets in the earlier section that there does not exist a non-empty set $S$ such that $S\approx \mathbb{N}_k$ for $\mathbb{N}_k$ . In other words, there does not exist a constant to express the number of elements of such set $S$ . Then, we can view infinitely many number of elements as an increasing state. In fact, there are two kinds of infinitely many numbers – one is countably many, or denumerable, and the other is uncountably many. First, we introduce the definition of denumerability.

Definition.
A denumerable set $S$ is defined as

$S\approx \mathbb{N}$

with $|S|=\aleph_0$

Let us explore the cardinality $\aleph_0$ with an example.

Example. Prove the set $\left\lbrace n:n\in \mathbb{N} \text{ and } n>5\right\rbrace$ is denumerable.

Proof.
Let $X=\left\lbrace n:n\in \mathbb{N} \text{ and } n>5\right\rbrace$ and define $f:X\rightarrow \mathbb{N}$ by $f(x)=x-5$ .

Suppose $f(x)=f(y)$ .
Then, $x-5=y-5$ .
Then, $x=y$ .
Therefore, $f$ is injective.

Let $n\in \mathbb{N}$ .
Choose $n+5\in X$ , so that $f(n+5)=(n+5)-5=n$ .
Then, $n\in Rng(f)$ .
Then, $\mathbb{N}\in Rng(f)$ .
Then, $\mathbb{N}= Rng(f)$ .
Therefore, $f$ is surjective.

Therefore, $f$ is bijective.
Then, there exists a bijection $f:X\rightarrow \mathbb{N}$ .
Therefore, $X\approx \mathbb{N}$ , and thus $|X|=\aleph_0$ .

Now, let us introduce a bigger infinite number, continuum $c$ , well demonstrated by the famous Cantor’s Diagonal Argument.

Definition.
An uncountable cardinal number $c$ , continuum, is defined as

$\left\vert (0,1) \right\vert=c$

Theorem. (Cantor’s Diagonal Argument)

Let $(0,1)=C$ .
Note that

$\mathbb{N}\approx \left\lbrace \frac{1}{3^k}:k\in \mathbb{N}\right\rbrace \subset C$

Therefore, $|C| \geq \aleph_0$ .

Suppose $|C| = \aleph_0$ .
Then, there exists a bijection $f:\mathbb{N} \rightarrow C$ .
Let us list the images of $f$ in normalized form:

$\begin{align*} f(1) &= 0.a_{11}a_{12}a_{13}\cdots\\ f(2) &= 0.a_{21}a_{22}a_{23}\cdots\\ f(3) &= 0.a_{31}a_{32}a_{33}\cdots\\ & \cdots\\ f(n) &= 0.a_{n1}a_{n2}a_{n3}\cdots\\ & \cdots \end{align*}$

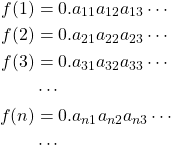
Now, let us define $b=0.b_1b_2b_3\cdots$ , where

$\begin{align*} b_i &= 1 \text{, if } a_{ii}\neq 1\\ &= 2 \text{, if } a_{ii}=1 \end{align*}$

Then, $b\in C$ .
However, $b\neq f(n)$ for all $n\in \mathbb{N}$ , since $b$ differs from $f(n)$ in the $n$ -th decimal place.
Therefore, $b\notin Rng(f)$ .
This is a contradiction, and thus $|C| \neq \aleph_0$ .

Then, $|C| > \aleph_0$ , since $|C| \neq \aleph_0$ .

Thinking of the cardinal number $c$ , in fact, every open interval is a continuum, summarized as:

Theorem.
$|(a,b)|=c$ for all $a,b\in R$ .

Let us illustrate with an example.

Example. Continuity of Real Numbers

Prove $\left\vert\mathbb{R}\right\vert=c$ .

Let us define a mapping $f:(0,1)\rightarrow\mathbb{R}$ by $f(x)=\tan\left( \pi\left(x-\frac{1}{2}\right)\right)$ .\\
Then, on $Dom(f)=(0,1)$ , this is a fractional linear transformation of one branch of the tangent function (Figure 1), and bijective to $\mathbb{R}$ .\\
Therefore, $(0,1)\approx\mathbb{R}$ .

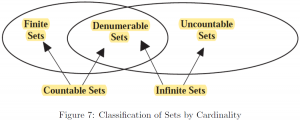
Thus, the sets by cardinality can be summarized as follows [14]:

15 Cardinality

Finite Sets

Infinite Sets

License

Share This Book