8 Section Summary

So far we have discussed the vast area of calculus, beginning from the limits and continuity, differential and integral calculus, and some applications, inclusive of differential equations. We also have expanded our purview to multivariate calculus with 2 or more independent variables, and explored some important sequences and series.

Indeed, within only about 20-page-long document, we cannot discuss all the relevant concepts in depth, but can only cover what we may call \emph{essentials} of calculus. Here the author notes there are so many areas of calculus to be explored.

To name a few, they are

• The use of calculus to parametric equations. Parametric equations refer to the equations independent and dependent variables are given as functions of a third variable, usually denoted by
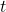
• The use of calculus on a polar coordinate system. Different from a regular 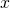– 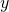coordinate system, polar coordinate system is based on radius and the angle 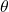from the polar axis
• More in partial differentiation; the concept of directional derivatives, gradient vector leads to
• Vector calculus, primarily concerned with differentiation and integration of vector fields in Euclidean space ;
• Usage in complex analysis; calculus of real-valued functions work well with complex functions a complex plane with only a bit of added/modified assumptions
• Multiple integrals; double, triple, or more integrals
• Usage in numerical analysis, where deterministic approach for a given equation is not ideal or possible
• Usage in differential equations; we only have discussed the first order linear differential equations, but not 2nd or higher order linear, and nonlinear differential equations

The list above is not exhaustive. Inclusive of them and more are just yet to be discovered by the reader.