2 Derivatives
The definition of a derivative can be given in two ways. Simply as the slope of a tangent line, or as the instantaneous rate of change in the dependent variable to the change of the independent variable. By saying instantaneous, we take the limit so that the interval of the independent variable be infinitesimal.
Formal definitions [10] are as follows:
Definition. (Derivative)
The derivative of a function ![]() at a number
at a number ![]() , denoted
, denoted ![]() , is defined as
, is defined as
(1) ![]()
given the limit is defined.
Alternatively, the derivative can also be defined as the slope ![]() of the tangent line to the curve
of the tangent line to the curve ![]() at the point
at the point ![]() :
:
(2) ![]()
again, given the limit is defined.
Note that the definitions (1) and (2) are equivalent. By letting ![]() , the equation (2) is obtained from the equation (1). In both cases, the derivative of
, the equation (2) is obtained from the equation (1). In both cases, the derivative of ![]() at
at ![]() refers to the ratio of the change in
refers to the ratio of the change in ![]() to the change in
to the change in ![]() by
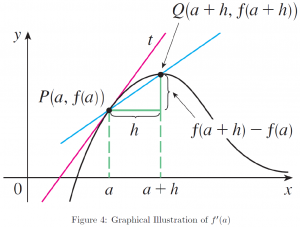
by ![]() . This is clearly shown in the following plot (Figure 4). As
. This is clearly shown in the following plot (Figure 4). As ![]() approaches
approaches ![]() , the blue line whose slope is the average ratio of change for the given interval
, the blue line whose slope is the average ratio of change for the given interval ![]() near
near ![]() , approaches the red line whose slope is the instantaneous ratio of change of
, approaches the red line whose slope is the instantaneous ratio of change of ![]() to
to ![]() at
at ![]() .
.
As was the case we expanded the notion of continuity at a point to continuity over a given interval or the whole domain of a given function, we can define the derivative of a whole function over its domain as follows [10]:
Definition. (Derivative of Function)
The derivative of a function ![]() ,
, ![]() is defined as
is defined as
![]()
given the limit is defined, i.e. exists, for ![]() .
.
Alternative notations for expressing derivatives are introduced here.
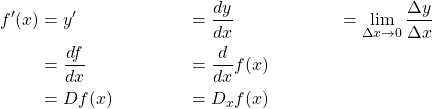
Let us illustrate with an example.
Example. Find the derivative of ![]() .
.
1. Express Derivative According to Definition
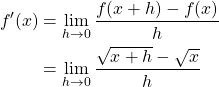
However, plugging in ![]() would only result in
would only result in ![]() , which is not defined, and thus we need to convert this into an equivalent expression by rationalization.
, which is not defined, and thus we need to convert this into an equivalent expression by rationalization.
2. Rationalize to Convert into Form that Can Be Evaluated
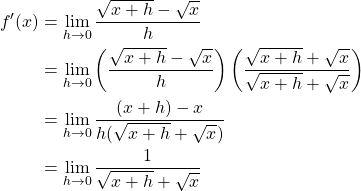
By rationalization, the form, ![]() , that could not have been evaluated, turned into the form that can be evaluated,
, that could not have been evaluated, turned into the form that can be evaluated, ![]() . Note that plugging in
. Note that plugging in ![]() does not result in an undefined expression.
does not result in an undefined expression.
3. Complete Evaluation by Inputting ![]()
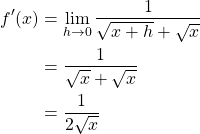
Therefore, we conclude ![]() .
.
Let us have a look at another example involving a trigonometric function.
Example. Find the derivative of ![]() , given
, given ![]() .
.
The basic strategy is essentially the same as the example above, as the initial form by definition only leads to an undefined ![]() . However, in this example we need to utilize trigonometric identities, since we are evaluating the limit of a trigonometric function, instead of an irrational function.
. However, in this example we need to utilize trigonometric identities, since we are evaluating the limit of a trigonometric function, instead of an irrational function.
1. Express Derivative According to Definition
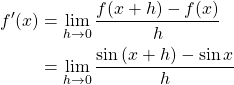
Again, plugging in ![]() would only result in
would only result in ![]() , which is not defined, and thus we need to convert this into an equivalent expression using trigonometric identities. We utilize one of sum identities,
, which is not defined, and thus we need to convert this into an equivalent expression using trigonometric identities. We utilize one of sum identities, ![]() .
.
2. Convert into Form that Can Be Evaluated with Trigonometric Identity
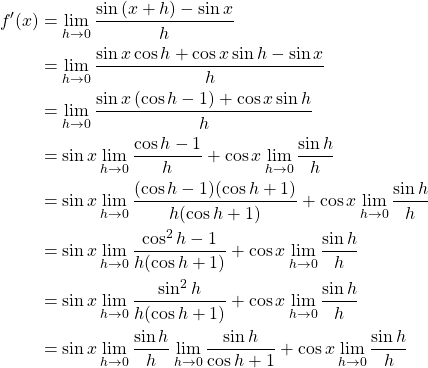
Using the sum identity of ![]() , the form,
, the form, ![]() , that could not have been evaluated, turned into the form that can be evaluated,
, that could not have been evaluated, turned into the form that can be evaluated, ![]() . Note that plugging in
. Note that plugging in ![]() does not result in an undefined expression.
does not result in an undefined expression.
3. Use Given Information ![]() .
.
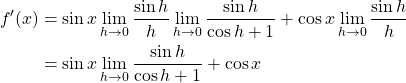
4. Complete Evaluation by Inputting ![]()
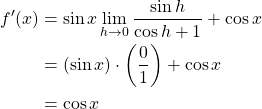
Therefore, we conclude ![]() .
.
To generalize, let us introduce and explore a few rules and patterns [10] observed when differentiating diverse functions, such as polynomials, and product of multiple functions.
Theorem. (Power Rule)
For any ![]() ,
,
![]()
Proof.
Let ![]() . Then,
. Then,
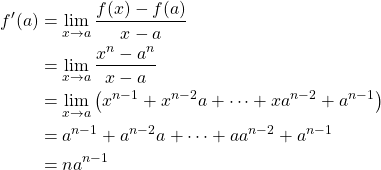
As we expanded our notion of a derivative at a point ![]() to a derivative of a function
to a derivative of a function ![]() , we substitute
, we substitute ![]() with
with ![]() . Therefore,
. Therefore,
![]()
Theorem. (Sum Rule)
If ![]() and
and ![]() are both differentiable, then
are both differentiable, then
![]()
Proof.
Let ![]() . Then,
. Then,
![Rendered by QuickLaTeX.com \begin{align*} F'(x) &= \lim_{h \to 0} \frac{F(x+h)-F(x)}{h}\\ &= \lim_{h \to 0} \left[\frac{\left[f(x+h)+g(x+h)\right]-\left[f(x)-g(x)\right]}{h}\right]\\ &= \lim_{h \to 0} \left[\frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\right]\\ &= \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}+\lim_{h \to 0} \frac{g(x+h)-g(x)}{h}\\ &= f'(x)+g'(x) \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9b4dd610ec10324cf52d683ae603214d_l3.png)
Theorem. (Product Rule)
If ![]() and
and ![]() are both differentiable, then
are both differentiable, then
![]()
Proof.
Let ![]() . Then,
. Then,
![Rendered by QuickLaTeX.com \begin{align*} F'(x) &= \lim_{h \to 0} \frac{F(x+h)-F(x)}{h}\\ &= \lim_{h \to 0} \frac{f(x+h)g(x+h)-f(x)g(x)}{h}\\ &= \lim_{h \to 0} \frac{f(x+h)g(x+h)-f(x+h)g(x)+f(x+h)g(x)-f(x)g(x)}{h}\\ &= \lim_{h \to 0} \frac{f(x+h)\left[g(x+h)-g(x)\right]+g(x)\left[f(x+h)-f(x)\right]}{h}\\ &= \lim_{h \to 0} \frac{f(x+h)\left[g(x+h)-g(x)\right]}{h}+\lim_{h \to 0}\frac{g(x)\left[f(x+h)-f(x)\right]}{h}\\ &= f(x)g'(x)+f'(x)g(x) \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1936023f0121f370ccc8577a26b08352_l3.png)
Chain Rule
The chain rule concerns the case of a composite function.
Theorem. (Chain Rule)
If ![]() is differentiable at
is differentiable at ![]() and
and ![]() is differentiable at
is differentiable at ![]() , then the composite function
, then the composite function ![]() is differentiable at
is differentiable at ![]() , and
, and
![]()
An alternative expression can be obtained by letting ![]() and
and ![]()
![]()
Let us illustrate with an example.
Example. Find ![]() , where
, where ![]() .
.
Let ![]() and
and ![]() . Then,
. Then,
![]()
Therefore,
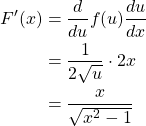
Here is another example involving an exponential function.
Example. Find ![]() , where
, where ![]() .
.
Let ![]() and
and ![]() . Then,
. Then,
![]()
Therefore,
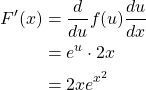
Implicit differentiation
So far we have only dealt with the differentiation of functions in the form of ![]() . However, at times, it is difficult or cumbersome to express the function in the form of
. However, at times, it is difficult or cumbersome to express the function in the form of ![]() , but instead, defined implicitly in the for of
, but instead, defined implicitly in the for of ![]() , as opposed to explicitly. Circle, for example,
, as opposed to explicitly. Circle, for example, ![]() , is a notable example.
, is a notable example.
Example. Find ![]() , where
, where ![]() .
.
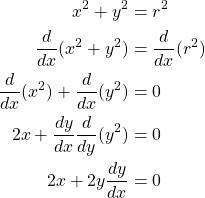
Therefore,
![]()
Another way of approaching the example above would be finding the explicit expression of ![]() in terms of
in terms of ![]() , and then differentiate. However, it would have been much more complex and prone to error involving differentiation of a composite square root function. Therefore, implicit differentiation can be a useful technique to avoid expensive computations.
, and then differentiate. However, it would have been much more complex and prone to error involving differentiation of a composite square root function. Therefore, implicit differentiation can be a useful technique to avoid expensive computations.
