7 Differential Equations
In this section, we discuss differential equations. Putting it simply, differential equations are equations with derivatives. Often this technique is utilized whenever a mathematical model is constructed. Let us explore with a familiar example, a free-fall of an object.
According to the Newton’s second law of motion,
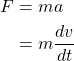
In the case of a free-fall, the net force applied is gravitational pull minus air resistance. That is,
![]()
where gamma is a drag coefficient.
By equalling both equations, we have
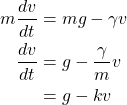
The final equation we have ![]() is a simple example of a differential equation. Before getting into more complex differential equations, let us first identify what kinds of differential equations are there.
is a simple example of a differential equation. Before getting into more complex differential equations, let us first identify what kinds of differential equations are there.
We can classify differential equations by order and linearity, i.e. whether the given differential equation is linear or nonlinear.
- Order
The order of the highest derivative included in the equation determines the order. That is, an -th order differential equation can be expressed as
-th order differential equation can be expressed as
![Rendered by QuickLaTeX.com \[ F\left( t,y,y',\cdots,y^{(n)}\right)=0\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-60720090b2a2f80d621c4456f1292be3_l3.png)
- Linearity
If a differential equation can be expressed as a linear function of![Rendered by QuickLaTeX.com \[y,y',\cdots,y^{(n)},\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-40adb441e7d583087e5a42fcc23cb2be_l3.png)
then it is a linear differential equation; otherwise, it is classified non-linear.
Let us clarify with some examples.
Example. Determine the order and the linearity of ![]() and
and ![]() .
.
We observe ![]() is a linear function of
is a linear function of ![]() , and
, and ![]() . As the highest order of derivative observed is
. As the highest order of derivative observed is ![]() , we conclude
, we conclude ![]() is a 2nd order linear differential equation.
is a 2nd order linear differential equation.
On the other hand, ![]() is not a linear function of derivatives, owing to the term
is not a linear function of derivatives, owing to the term ![]() . Therefore,
. Therefore, ![]() is a 1st order non-linear differential equation.
is a 1st order non-linear differential equation.
Let us further explore the 1st-order linear differential equations. The 1st-order linear differential equation in the standard form would look
![]()
Recall the product rule ![]() in a former section. Then, if a differential equation is in a form
in a former section. Then, if a differential equation is in a form
![]()
we can immediately integrate both sides and easily solve for ![]() . In this case,
. In this case, ![]() is called an integrating factor.
is called an integrating factor.
Let us illustrate with an example.
Example. Find the general solution of the differential equation
![]()
Let ![]() be an integrating factor. Then,
be an integrating factor. Then,
![]()
We need to find ![]() such that
such that ![]() .
.
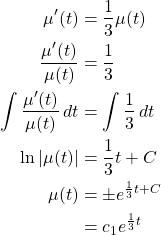
Therefore,
![]()
Therefore,
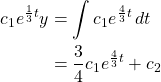
Therefore,
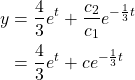
We conclude this section here, as higher order and nonlinear differential equations are much more complex and cannot be dealt with elementary-level calculus.
