Functions

Donovan D Chang

14 Functions

Long awaited, you might as well have wondered why we have been studying the set theory and relations. In fact, it was to have an in-depth understanding of a function, one of the most important and core concepts in mathematics. One way of understanding a function is by viewing functions as “single-valued relations”, i.e. only one value of $y$ is assigned to each $x$ for $(x,y)\in R$ . Also, it is customary to substitute $R$ with a small case letter such as $f$ . Let us formally define a function.

Definition. (Function or Mapping)
A function or mapping from $A$ to $B$ , denoted $f:A\rightarrow B$ , is a relation $f$ from $A$ to $B$ such that
* $Dom(f)=A$ ; and
* $(x,y),(x,z)\in f\Rightarrow (y=z)$

The equality of functions $f$ and $g$ are proven using the usual strategy to prove both $f\subseteq g$ and $g\subseteq f$ . Here we introduce a shortcut.

Theorem. (The Equality of Functions)
Functions $f$ and $g$ are equal iff
* $Dom(f)=Dom(g)$ and
* $f(x)=g(x)$ for all $x\in Dom(f)$

Let us illustrate with an example.

Example. Examine the equality of real-valued functions $f$ and $g$ defined by

$f(x)=\frac{1}{x} \text{ and } g(x)=\frac{x}{x^2}$

Let us examine the domain of each function.
$Dom(f)=\mathbb{R}- \left\lbrace 0 \right\rbrace$ , since $x \neq 0$ .
Also, $Dom(g)=\mathbb{R}- \left\lbrace 0 \right\rbrace$ , since $x^2 \neq 0$ .
Therefore, $Dom(f)=Dom(g)=\mathbb{R}-\left\lbrace 0 \right\rbrace$ .

$\frac{1}{x}=\frac{x}{x^2}$ for all $x\in \mathbb{R}-\left\lbrace 0 \right\rbrace$ .

Therefore, $f=g$ .

In fact, functions can be classified into one of the following categories:
1. Injection or One-to-One Function, that every element in the range of the function is corresponded only once.
2. Surjection or Onto Function, that every element in the codomain is corresponded.
3. Bijection or One-to-One Correspondence, that a given function is both injective and surjective.

The details of each function mentioned above will be discussed in the following subsections.

One-to-One Functions

The mapping $f:A\rightarrow B$ is one-to-one or injective, written $f:A\,\underrightarrow{\text{1-1}}\,B$ , if

$f(x)=f(y)\,\Rightarrow \, (x=y)$

Let us illustrate with an example.

Example. Show that $f:\mathbb{R}\rightarrow \mathbb{R}$ defined by $f(x)=x^3$ is injective.

We must show $f(x)=f(y)\,\Rightarrow \, (x=y)$ for $x,y\in \mathbb{R}$ .

Let $f(x)=f(y)$ where $x,y\in \mathbb{R}$ .
Then,

$\begin{align*} f(x) &= f(y)\\ x^3 &= y^3\\ \left( x^3\right)^\frac{1}{3} &= \left( y^3\right)^\frac{1}{3}\\ x &= y \end{align*}$

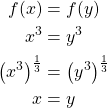
Therefore, $f(x)=f(y)\,\Rightarrow \, (x=y)$ .
Therefore, $f$ is injective.

A useful theorem is the composite of injective functions is again an injection. That is,

Theorem.
If $f:A\,\underrightarrow{\text{1-1}}\,B$ and $g:B\,\underrightarrow{\text{1-1}}\,C$ , then $g\circ f:A\,\underrightarrow{\text{1-1}}\,C$

It is intuitive this has to be the case, since $g$ is injective, every element of $B$ corresponds to the different element of $C$ . And since $Rng(f)\subseteq B$ , the subset of $B$ will always be injective.

Onto Functions

The mapping $f:A\rightarrow B$ is onto or surjective, written $f:A\,\underrightarrow{\text{onto}}\,B$ , if

$Rng(f)=B$

Let us revisit the example.

Example. Show that $f:\mathbb{R}\rightarrow \mathbb{R}$ defined by $f(x)=x^3$ is surjective.

We must show $Rng(f)=\mathbb{R}$ .
In fact, by definition $Rng(f) \subseteq \mathbb{R}$ .
Therefore, it suffices to show $\mathbb{R} \subseteq Rng(f)$ .

Let $r\in \mathbb{R}$ .
Then, $r^\frac{1}{3}\in \mathbb{R}$ .
Indeed, $\left( r^\frac{1}{3}\right)^3=r$ .
Therefore, there exists $r^\frac{1}{3} \in \mathbb{R}$ such that $\left( r^\frac{1}{3}\right)^3=r\in \mathbb{R}$ .
Therefore, $\mathbb{R} \subseteq Rng(f)$ .
Therefore, $Rng(f)=\mathbb{R}$ .
Therefore, $f$ is surjective.

As in the case of injection, the composite of surjective functions is again a surjection. That is,

Theorem.
If $f:A\,\underrightarrow{\text{onto}}\,B$ and $g:B\,\underrightarrow{\text{onto}}\,C$ , then $g\circ f:A\,\underrightarrow{\text{onto}}\,C$

It is intuitive this has to be the case, since $g$ is surjective, $Rng(g)=C$ . And since $f$ also is surjective, $Rng(f)=B$ , and thus $g \circ f$ is surjective.

One-to-One Correspondence

The mapping $f:A\rightarrow B$ is one-to-one correspondence or bijective, written $f:A\,\xrightarrow[1-1]{\text{onto}}\,B$ , if

$Rng(f)=B$ and $f(x)=f(y)\,\Rightarrow \, (x=y)$

i.e. both surjective and injective.

Let us illustrate with an example.

Example. Show that $f:\mathbb{R} \rightarrow \mathbb{R}^+$ defined by $f(x)=e^x$ is bijective.

Proof.
We must show
1. Surjectivity of $f$ , $Rng(f)=\mathbb{R}^+$

In fact, by definition $Rng(f) \subseteq \mathbb{R}^+$ .
Therefore, it suffices to show $\mathbb{R}^+ \subseteq Rng(f)$ .

Let $y\in \mathbb{R}^+$ , i.e. $y>0$ .
Then, $\ln y \in \mathbb{R}$ .
Then, there exists $\ln y\in \mathbb{R}$ such that $e^{\ln y}=y$ .
Then, $Rng(f)=\mathbb{R}^+$ .
Therefore, $f$ is surjective.

2. Injectivity of $f$ , $f(x)=f(y)\,\Rightarrow \, (x=y)$

Let $f(x)=f(y)$ where $x,y\in \mathbb{R}$ .
Then,

$\begin{align*} f(x) &= f(y)\\ e^x &= e^y\\ \ln \left( e^x\right) &= \ln \left( e^y\right)\\ x &= y \end{align*}$

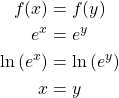
Therefore, $f(x)=f(y)\,\Rightarrow \, (x=y)$ .
Therefore, $f$ is injective.

Therefore, by 1. and 2., $f$ is bijective.

As in the case of surjection and injection, the composite of bijective functions is again a bijection. That is,

Theorem.
If $f:A\,\xrightarrow[1-1]{\text{onto}}\,B$ and $g:B\,\xrightarrow[1-1]{\text{onto}}\,C$ , then $g\circ f:A\,\xrightarrow[1-1]{\text{onto}}\,C$

It is intuitive this has to be the case, since $g$ is surjective, $Rng(g)=C$ . And since $f$ also is surjective, $Rng(f)=B$ , and thus $g \circ f$ is surjective. Also, since $g$ is injective, every element of $B$ corresponds to the different element of $C$ . And since $Rng(f)\subseteq B$ , the subset of $B$ will always be injective.

Studying mathematics so far, you might as well have heard of a term, inverse function. However, an inverse relation is not necessarily a function. Let us recall the definition of a function first. For $f:A\rightarrow B$ to be a function, $Dom(f)=A$ and $(x,y),(x,z)\in f\Rightarrow (y=z)$ . Therefore, for its inverse $f^{-1}$ to be a function, $Dom(f^{-1})=B$ and
$(y,x),(y,z)\in f^{-1}\Rightarrow (x=z)$ .

In fact, the monotonicity, formerly introduced in the Calculus section, of a function is required for the given function to have an inverse. Let us recall the definition of monotonic sequence.

A sequence is called monotonic when either increasing or decreasing
1. $a_n < a_{n+1}$ for all $n\in \mathbb{N}$
2. $a_n > a_{n+1}$ for all $n\in \mathbb{N}$

When this definition is adapted to into the context of functions, this becomes:

A function is called monotonic when either increasing or decreasing. That is,
1. $f(x) < f(y)$ for $x<y$
2. $f(x) > f(y)$ for $x<y$

Notice the similarity in definitions above. Each number in the sequence corresponds to each element in $Rng(f)$ , and the increasing the value of elements in $Dom(f)$ defined by $x<y$ is embedded in the expression $n\in \mathbb{N}$ , as natural numbers are already well-ordered.

This is just one showcasing example reflecting the interconnectedness of mathematics. The concept of monotonicity was revisited here, and will again be revisited in the following section, Real Analysis. Thus it is crucial to fully understand key concepts, as they are building blocks of mathematics.

14 Functions

One-to-One Functions

Onto Functions

One-to-One Correspondence

License

Share This Book