22 Groups
We first define a group, the unit where a binary operation is defined.
Definition. (Group)
A group ![]() is a set
is a set ![]() , closed under a binary operation
, closed under a binary operation ![]() , satisfying the following axioms:
, satisfying the following axioms:
1. Associativity
For all ![]() ,
,
![]()
2. The Existence of Identity Element
For all ![]() , there exists an identity element
, there exists an identity element ![]() such that
such that
![]()
3. The Existence of Inverse of Each Element
For all ![]() , there exists an inverse
, there exists an inverse ![]() of
of ![]() such that
such that
![]()
We know associativity is the property of addition and multiplication. However, note this is the case because addition and multiplication each is a binary operation, not an inherent property of these operations. With respect to identity element and inverse, they are ![]() and
and ![]() for
for ![]() in addition, and
in addition, and ![]() and
and ![]() for
for ![]() in multiplication.
in multiplication.
Then, what is a binary operation?
Definition. (Binary Operation)
A binary operation ![]() on a set
on a set ![]() is a mapping
is a mapping ![]() . Conventionally, we denote
. Conventionally, we denote ![]() as
as
![]()
Note that, by definition, a given binary operation is closed. That is, any pair of elements under the operation in ![]() is also in
is also in ![]() .
.
Let us have a look at some examples.
Example. Determine whether the operation ![]() defined by
defined by ![]() on
on ![]() is binary.
is binary.
Let ![]() .
.
Suppose ![]() .
.
Then, ![]() .
.
Then, ![]() is not defined in
is not defined in ![]() , but defined as
, but defined as ![]() in
in ![]() .
.
Therefore, ![]() is not closed.
is not closed.
Therefore, ![]() is not a binary operation.
is not a binary operation.
Example. Determine whether ![]() is a group for a binary operation
is a group for a binary operation ![]() defined on
defined on ![]() as
as ![]() .
.
Let ![]() .
.
Then,
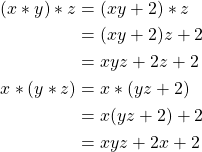
Therefore, ![]() .
.
Therefore, ![]() is not associative.
is not associative.
Therefore, ![]() is not a group.
is not a group.
In fact, the left and right cancellation laws are the result of a given set, together with an operation, being a group.
Theorem. (Left and Right Cancellation Laws of Binary Operation)
Given a group ![]() ,
,
![]()
![]()
Proof.
1. ![]()
Suppose ![]() .\\
.\\
Then,
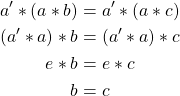
2. ![]()
Suppose ![]() .
.
Then,
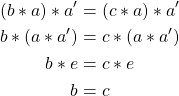
As we defined a subset of a set, we can also define a subgroup of a group. Since a group is itself already a set by definition, a subgroup is a subset of a group meeting the axioms of a group. Therefore,
Definition. (Subgroup)
Let ![]() be a group. If
be a group. If ![]() is also a group, where
is also a group, where ![]() , then,
, then, ![]() is a subgroup of
is a subgroup of ![]() , and we denote
, and we denote
![]()
Let us illustrate with an example.
It was formerly discussed the set of real numbers ![]() is a commutative division ring. Considering only one operation, addition (
is a commutative division ring. Considering only one operation, addition (![]() ),
), ![]() can be viewed as a group, meeting all three axioms of group.
can be viewed as a group, meeting all three axioms of group.
- Indeed, addition (
 ) is associative.
) is associative. - The identity element of addition,
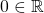
 for all
for all 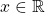 so that
so that
![Rendered by QuickLaTeX.com \[ (-x)+x=x+(-x)=0\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7a82c87578ecda0913d74e88c45e1a99_l3.png)
In fact, the same holds for the set of integers ![]() . That is, (i) addition of integers is associative; (ii) The identity element of addition,
. That is, (i) addition of integers is associative; (ii) The identity element of addition, ![]() ; and (iii)
; and (iii) ![]() for all
for all ![]() so that
so that ![]() . Note that the axiom (iii) holds even when
. Note that the axiom (iii) holds even when ![]() , since
, since ![]() .
.
Therefore, we conclude ![]() .
.
In fact, there is a shortcut in examining or proving whether a given set is a subgroup as follows:
Theorem.
![]() , or simply
, or simply ![]() , iff
, iff
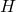 is closed under the binary operation
is closed under the binary operation  of
of 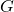 , where
, where 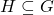
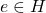 , where
, where  is the identity element of
is the identity element of 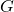
- for every
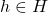 , its inverse
, its inverse 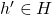
The only difference of this theorem with the definition of a subgroup is the associativity requirement is replaced with checking whether ![]() is closed under
is closed under ![]() , the binary operation of interest. This confirmation suffices to establish associativity, since
, the binary operation of interest. This confirmation suffices to establish associativity, since ![]() , the mother set of
, the mother set of ![]() , is already a group, and thus it is implied by definition of a group that associativity holds for
, is already a group, and thus it is implied by definition of a group that associativity holds for ![]() .
.
Cyclic Subgroups
There is a special case of subgroup called cyclic subgroup. Let us illustrate with an example.
Consider a set
![]()
In fact, ![]() , though small, is a subgroup.
, though small, is a subgroup.
Now, let us take another approach. Suppose we want to construct a \emph{smallest subgroup} ![]() of
of ![]() containing
containing ![]() . Then, we can take the following steps, utilizing the subgroup theorem:
. Then, we can take the following steps, utilizing the subgroup theorem:
- We begin from
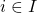 .
. - Then, keep multiplying by
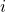 and include all the products in
and include all the products in 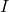 .
. - Soon, we shall find a pattern the multiplication is \emph{cyclic} with
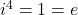 .
. - In fact, we also have to include any combination of the products in
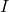 to ensure
to ensure 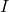 be closed under the operation (
be closed under the operation ( ). However, this is not necessary since, again, we see a cyclic pattern.
). However, this is not necessary since, again, we see a cyclic pattern. - As the multiplication of
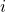 is cyclic, for all
is cyclic, for all  , where
, where 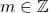 , its inverse
, its inverse 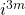 is also in
is also in 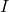 , since
, since
![Rendered by QuickLaTeX.com \[ i^m\cdot i^{3m}=i^{3m}\cdot i^m=i^{4m}=1\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3b1ae5b3031936bf939a009971c4848e_l3.png)
Therefore, we conclude we constructed a subgroup ![]() by the subgroup theorem. Also, since we began with only one element,
by the subgroup theorem. Also, since we began with only one element, ![]() , this is the smallest subgroup generated by
, this is the smallest subgroup generated by ![]() . We provide a formal definition as follows.
. We provide a formal definition as follows.
Definition. (Cyclic Subgroup and Generator)
Let ![]() , where
, where ![]() is a group. Then,
is a group. Then,
![]()
is called a cyclic subgroup ![]() of
of ![]() generated by
generated by ![]() , where
, where ![]() is called a generator.
is called a generator.
Note that a cyclic group need not be finite. One simple example of an infinite cyclic group would be
![]()
where the operation of interest is addition (![]() ). We know
). We know ![]() is denumerable with
is denumerable with ![]() .
.
Isomorphism
Now we turn our attention to isomorphism. Recall our discussion at the very beginning of this section that our focus is on the algebraic structure rather than the results of arithmetic operations themselves or obtaining solutions.
Let us revisit the example provided in the introduction. We saw a pattern that
- Zero (0) in addition corresponds to 1 in multiplication, serving as an identity element of a given operation.
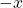 in addition corresponds to
in addition corresponds to 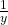 for
for 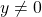 in multiplication, serving as an inverse of a given operation.
in multiplication, serving as an inverse of a given operation.
The pattern we observed can be summarized as follows:
![Rendered by QuickLaTeX.com \[\begin{array}{l|ccc} & \textbf{Addition }(+) & \textbf{Multiplication }(\cdot) & \textbf{Binary Operation} (*) \\ \hline \textbf{Element} & x & y & z \\ \textbf{Identity} & 0 & 1 & e \\ \textbf{Inverse} & -x & \frac{1}{y} & z' \\ \end{array}\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-302eadae2fd0c9e92ff8e50f547af641_l3.png)
What if it is possible to connect or correspond every element in one group to every element in another group, bijectively, while preserving the algebraic structure, i.e. in a homomorphic manner? Such case is called isomorphism, and formally defined as follows:
Definition. (Isomorphism)
An isomorphism of a group ![]() with a group
with a group ![]() , denoted
, denoted
![]()
is a bijective function ![]() that is also a homomorphism:
that is also a homomorphism:
![]()
Naturally, how to demonstrate isomorphism is to first show there exists a bijective mapping between the two groups, and then examine for homomorphism. Let us illustrate with an example.
Examine whether ![]() , where
, where ![]() , defined by
, defined by ![]() is isomorphic.
is isomorphic.
- Examine whether
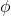 is bijective
is bijective
- Surjectivity
Let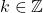 .
.
Then,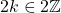 by definition.
by definition.
In fact,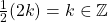 .
.
Then, there exists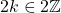 such that
such that
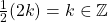 .
.
Therefore,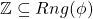
Therefore,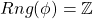 , and thus
, and thus 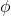 is surjective.
is surjective. - Injectivity
Suppose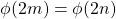 .
.
Then,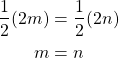
Therefore,
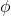 is injective.
is injective.
- Surjectivity
- Examine homomorphism
This is a simple computation problem. We only need to check whether
![Rendered by QuickLaTeX.com \[ \phi (m\cdot n)=\phi (m)\cdot \phi(n)\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-014f68a4ffe8226d725888a4ab469637_l3.png)
Let us examine.
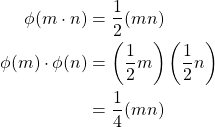
Therefore,
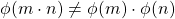 .
.
Therefore, ![]() is not an isomorphism, since
is not an isomorphism, since ![]() is not homomorphic.
is not homomorphic.
Structural Properties are shared over isomorphism
An important thing to note about isomorphism is isomorphism carries structural properties. That is, the structural properties found in one group also have to be found in an isomorphic group. One example of a structural property is cardinality, the number of elements. Indeed cardinality is shared, since, by definition, isomorphism is a bijection with a homomorphic property.
Factor Groups
In this section, we introduce a few mathematical concepts of organizing or decomposing the elements of a given group. One way is to decompose a group as a Cartesian product of finitely many groups – note that we apply in the context of abelian or commutative groups.
Another way is by focusing on a homomorphic property. Suppose we specify a subgroup ![]() of a group
of a group ![]() . Then, either by a left-side or right-side operation, the mother group
. Then, either by a left-side or right-side operation, the mother group ![]() will be partitioned into equal-size pieces called cosets. When these left- and right-cosets are the same, then this subgroup is normal.
will be partitioned into equal-size pieces called cosets. When these left- and right-cosets are the same, then this subgroup is normal.
A special case of a subgroup ![]() is kernel. That is,
is kernel. That is, ![]() is the collection of elements homomorphically mapped via
is the collection of elements homomorphically mapped via ![]() to the identity element of another group, say,
to the identity element of another group, say, ![]() . Then, this subgroup
. Then, this subgroup ![]() , or
, or ![]() , is also normal, and the cosets of the kernel
, is also normal, and the cosets of the kernel ![]() themselves form a group called a quotient group or factor group.
themselves form a group called a quotient group or factor group.
We conclude this chapter by showing how a group, its quotient group, and the set of the images of a homomorphic mapping are related.
Let us begin with introducing the direct product of the groups.
Definition. (Direct Product of the Groups)
The direct product of groups ![]() is defined as
is defined as
![]()
where ![]() denotes the Cartesian product of sets.
denotes the Cartesian product of sets.
The binary operation on ![]() defined as
defined as
![]()
Therefore, a group is formed by the direct product of groups, since ![]() for all
for all ![]() , and thus
, and thus ![]() .
.
For a special case when a direct product is defined on an abelian group ![]() (that is,
(that is, ![]() for all
for all ![]() ), this group is isomorphic to a direct product of cyclic groups as the Fundamental Theorem of Finitely Generated Abelian Groups [9] states as follows:
), this group is isomorphic to a direct product of cyclic groups as the Fundamental Theorem of Finitely Generated Abelian Groups [9] states as follows:
Theorem. (Fundamental Theorem of Finitely Generated Abelian Groups)
Every finitely generated abelian group ![]() is isomorphic to a direct product of cyclic groups in the form
is isomorphic to a direct product of cyclic groups in the form
![]()
where ![]() ‘s are primes, allowed for duplicates, and
‘s are primes, allowed for duplicates, and ![]() .
.
Let us apply this theorem with an example.
Example. Find all abelian groups of order 36.
Let us first decompose the number ![]() into prime factors.
into prime factors.
![]()
Then, begin from assigning all ![]() ‘s to 1, and consider cases where
‘s to 1, and consider cases where ![]() ‘s can be increased.
‘s can be increased.
![]()
![]()
![]()
![]()
Therefore, we conclude there are 4 different abelian groups of order 36, up to isomorphism.
Now we turn our attention to partitioning a group focusing on homomorphic property. To begin with, we introduce the concept of cosets.
Definition. (Left- and Right- Cosets)
For ![]() and
and ![]() , define the left- and right-coset of
, define the left- and right-coset of ![]() as
as
![]()
In fact, every coset, either left or right, has the same cardinality as ![]() . Therefore, for a finite group
. Therefore, for a finite group ![]() , where
, where ![]() ,
,
![]()
This is called the Theorem of Lagrange.
What’s next?
Now, we introduce a kernel, a special case of a normal subgroup whose elements are mapped to the identity element of another group in a homomorphic way. Formal definition is as follows:
Definition. (Kernel)
Given a homomorphic mapping ![]() , the \textbf{kernel} of
, the \textbf{kernel} of ![]() is defined as
is defined as
![]()
Therefore, it naturally follows the set defined by
![]()
is in fact a coset ![]() , where
, where ![]() . Recall a kernel is a special case of a normal subgroup and thus
. Recall a kernel is a special case of a normal subgroup and thus ![]() .
.
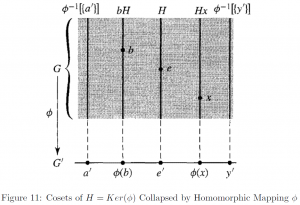
Let us illustrate with an image [9] what the introduced concepts mean. We can think of the elements in each coset are collapsed or projected into a single element in ![]() . Therefore, we can define a bijective mapping
. Therefore, we can define a bijective mapping ![]() , linking each coset to the image under
, linking each coset to the image under ![]() , and reach the following theorem, the Fundamental Homomorphism Theorem [9].
, and reach the following theorem, the Fundamental Homomorphism Theorem [9].
Theorem. (Fundamental Homomorphism Theorem)
Let ![]() be a group homomorphic mapping, and let
be a group homomorphic mapping, and let ![]() .
.
Then,
![Rendered by QuickLaTeX.com \phi[G]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1f195e3483569e42596bb8be13660c2e_l3.png) is a group, and
is a group, and![Rendered by QuickLaTeX.com G/H \simeq \phi[G]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-607f51c14928265a69d860126615a47e_l3.png) , since we can define a bijective mapping
, since we can define a bijective mapping 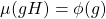 .
.
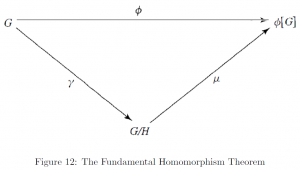
Therefore, in sum, a triangle is formed between a group ![]() , the image set
, the image set ![]() of
of ![]() under a homomorphic mapping
under a homomorphic mapping ![]() , the quotient group
, the quotient group ![]() of
of ![]() over the kernel
over the kernel ![]() :
:
- The mapping
![Rendered by QuickLaTeX.com \phi:G\rightarrow \phi[G]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9f0bf532c1165b533698477e4b26d6e0_l3.png) is homomorphic, collapsing each element of cosets of its kernel into a corresponding image
is homomorphic, collapsing each element of cosets of its kernel into a corresponding image - The mapping
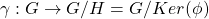 is homomorphic, partitioning elements of
is homomorphic, partitioning elements of 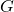 into cosets of
into cosets of 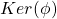
- The mapping
![Rendered by QuickLaTeX.com \mu:G/H=G/Ker(\phi)\rightarrow \phi[G]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a1474cb0a36dffb0e0281215a1e92550_l3.png) is isomorphic, connecting each coset formed by
is isomorphic, connecting each coset formed by 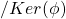 , treated as an element in this context, with the corresponding image in
, treated as an element in this context, with the corresponding image in ![Rendered by QuickLaTeX.com \phi[G]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1f195e3483569e42596bb8be13660c2e_l3.png)
The homomorphism ![]() and isomorphism
and isomorphism ![]() is called natural or canonical homomorphism and isomorphism, respectively.
is called natural or canonical homomorphism and isomorphism, respectively.
