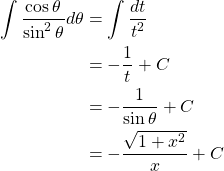3 Integrals
At the very beginning of this article, we briefly introduced integration, a crucial part of integral calculus, as the summation of infinitesimal differences. When these infinitesimal differences refer to lines or curves, then the product, the summed result is the area under the curve of a given function; when referring to surfaces, the result is a volume; and so forth.
Let us first introduce a definite integral. A definite integral of a function ![]() from
from ![]() to
to ![]() is denoted as
is denoted as
![]()
provided ![]() is a continuous function defined on
is a continuous function defined on ![]() .
.
A definite integral is commonly referred to as the area under the curve. However, this is only a result, but a more intuitive way of understanding is as a multiplication of infinitesimal difference (![]() ) with varying, i.e. changing, values of a function.
) with varying, i.e. changing, values of a function.
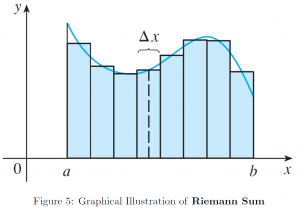
A classic way of approximating a definite integral is the famous Riemann sum. Riemann sum is computed as the sum of areas partitioned into ![]() rectangles, trapezoids, or other shapes of choice. When this
rectangles, trapezoids, or other shapes of choice. When this ![]() goes to
goes to ![]() , the Riemann sum becomes a definite integral.
, the Riemann sum becomes a definite integral.
Let us illustrate the Riemann sum with an example [10].
Example. Find the Riemann sum of a continuous function ![]() on the interval
on the interval ![]() .
.
First, we divide the interval into ![]() equally spaced subintervals by letting
equally spaced subintervals by letting
![]()
Then, we have ![]() , where
, where ![]() ,
,
for ![]() .
.
Then, we have the approximate ![]() -th strip area of a rectangle with width
-th strip area of a rectangle with width ![]() and height
and height ![]() (Figure 5 [10]). Therefore, the Riemann sum
(Figure 5 [10]). Therefore, the Riemann sum ![]() is
is
![]()
Now we formally define the the area ![]() under the curve on a given interval [10].
under the curve on a given interval [10].
Definition. (Area under Curve)
The area ![]() under the curve on the given interval of a continuous function
under the curve on the given interval of a continuous function ![]() is the limit of the Riemann sum. That is,
is the limit of the Riemann sum. That is,
![Rendered by QuickLaTeX.com \begin{align*} S &= \lim_{n \to \infty} R_n\\ &= \lim_{n \to \infty} \left[ f(x_1)\Delta x+f(x_2)\Delta x+\cdots+f(x_n)\Delta x\right]\\ &= \lim_{n \to \infty} \left[ \Sigma_{k=1}^{n} f(x_k)\Delta x\right] \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-32ded51ac609f17a22f80ce63a757a67_l3.png)
In fact, we can approximate the Riemann sum with the left-hand side height of a given strip, where ![]() denotes the rectangles with a left-hand side height, i.e.
denotes the rectangles with a left-hand side height, i.e.
![Rendered by QuickLaTeX.com \begin{align*} S &= \lim_{n \to \infty} L_n\\ &= \lim_{n \to \infty} \left[ f(x_0)\Delta x+f(x_1)\Delta x+\cdots+f(x_{n-1})\Delta x\right]\\ &= \lim_{n \to \infty} \Sigma_{k=0}^{n-1} \left[f(x_{k})\Delta x\right] \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6bf03f93e603d4848c33621ab91f25c5_l3.png)
Consequently,
Definition. (Definite Integral)
The definite integral of ![]() from
from ![]() to
to ![]() is
is
![Rendered by QuickLaTeX.com \begin{align*} \int_{a}^{b} f(x)dx &= \lim_{n \to \infty} \left[ f(x_0)\Delta x+f(x_1)\Delta x+\cdots+f(x_{n-1})\Delta x\right]\\ &= \lim_{n \to \infty} \left[ f(x_1)\Delta x+f(x_2)\Delta x+\cdots+f(x_n)\Delta x\right]\\ &= \lim_{n \to \infty} \Sigma_{k=0}^{n-1} \left[f(x_{k})\Delta x\right]\\ &= \lim_{n \to \infty} \Sigma_{k=1}^{n} \left[f(x_{k})\Delta x\right] \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-29253863796b9dc980f5a65c7505b474_l3.png)
As opposed to the area under the curve, in fact a \textbf{definite integral}, let us now think of a function ![]() whose derivative
whose derivative ![]() is an integrand, the function to be integrated. The integrated product
is an integrand, the function to be integrated. The integrated product ![]() is called the antiderivative of
is called the antiderivative of ![]() and we express this in the form of an indefinite integral as follows
and we express this in the form of an indefinite integral as follows
![]()
Some commonly used indefinite integrals are provided as follows [10].
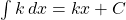
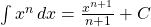 , where
, where 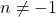
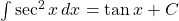
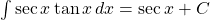
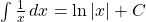
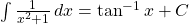
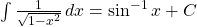
Remark
The latter two, ![]() and
and ![]() , will be discussed in the later section, Trigonometric Substitution.
, will be discussed in the later section, Trigonometric Substitution.
The veracity of these antiderivatives can be confirmed by taking the derivative. Let us explore a few examples and then discover a few rules of integration.
Example. Verify ![]() .
.
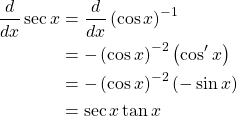
Here is another example.
Example. Verify ![]() .
.
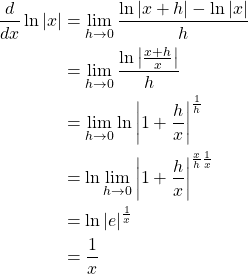
Recall the chain rule in the Derivatives section. The inverse of the chain rule in integration is called the substitution rule. That is,
Theorem. (Substitution Rule)
If ![]() is a differentiable function with a range, an interval
is a differentiable function with a range, an interval ![]() , and
, and ![]() is continuous on
is continuous on ![]() , then
, then
![]()
Let us illustrate with an example.
Example. Find ![]() .
.
Let ![]() . Then,
. Then, ![]() . Then,
. Then,
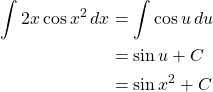
Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus is a bridge connecting differential and integral calculus, and is divided into 2 parts. The first part establishes the interconnection between the two, that one of the antiderivates, denoted by ![]() , of an integrable function
, of an integrable function ![]() can be obtained as a definite integral of
can be obtained as a definite integral of ![]() . The second part, called Newton-Leibniz axiom, a definite integral of
. The second part, called Newton-Leibniz axiom, a definite integral of ![]() can be computed by any one antiderivative
can be computed by any one antiderivative ![]() of its infinitely many antiderivatives.
of its infinitely many antiderivatives.
Theorem. (Fundamental Theorem of Calculus)
Part 1.
If ![]() is continuous on
is continuous on ![]() , then the function
, then the function ![]() defined by
defined by
![]()
is continuous on ![]() and differentiable on
and differentiable on ![]() , and
, and
![]()
Part 2.
If ![]() is continuous on
is continuous on ![]() , then
, then
![]()
where ![]() .
.
Integration by Parts
Recall the product rule of integration. That is,
![Rendered by QuickLaTeX.com \begin{align*} \frac{d}{dx}\left[f(x)g(x)\right] &=f(x)\frac{d}{dx}g(x)+g(x)\frac{d}{dx}f(x)\\ &=f(x)g'(x)+f'(x)g(x) \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1a3674e210af1a08d6c1f6c314bb48b2_l3.png)
Then, by integrating both sides,
![Rendered by QuickLaTeX.com \begin{align*} f(x)g(x) &= \int \left[f(x)g'(x)+f'(x)g(x)\right]\,dx\\ &= \int f(x)g'(x)\,dx + \int f'(x)g(x)\,dx \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bf68c5038c6d0e805dcefca81cee750a_l3.png)
Therefore,
![]()
This can alternatively be expressed as follows, by letting ![]() and
and ![]() :
:
![]()
Let us illustrate with an example.
Example. Find ![]() .
.
Let ![]() and
and ![]() .
.
Then, ![]() and
and ![]() .
.
Then,
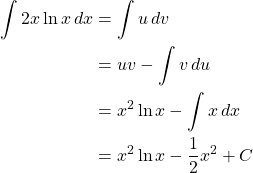
Trigonometric Substitution
We can in fact inversely substitute ![]() with another function
with another function ![]() , so that
, so that
![]()
This line of trick or technique is useful whenever we encounter the following cases:
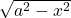 . \quad Let
. \quad Let 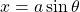 for
for ![Rendered by QuickLaTeX.com \theta \in \left[ -\frac{\pi}{2},\frac{\pi}{2} \right]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8259956c6d03eafc0e28c47eae36c6b2_l3.png)
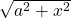 . \quad Let
. \quad Let 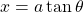 for
for 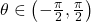
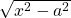 . \quad Let
. \quad Let 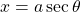 for
for 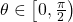 or
or 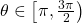
It would be easier to illustrate with examples.
Example. Evaluate ![]() .
.
Let ![]() for
for ![]() . Then,
. Then, ![]() . Then,
. Then,
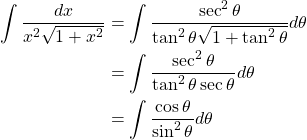
Now, let ![]() . Then,
. Then, ![]() . Then,
. Then,