1 Limits and Continuity
To discuss integration and differentiation, we need to introduce and understand the notions of limits and continuity. Let us begin with an intuitive definition of a limit from the Stewart’s Calculus Textbook.
Definition (Intuitive Definition of Limit)
Suppose ![]() is defined on an interval
is defined on an interval ![]() , and let
, and let ![]() . When
. When ![]() is near
is near ![]() , and the value of
, and the value of ![]() is near
is near ![]() , then we write
, then we write
![]()
and say “the limit of ![]() , as
, as ![]() approaches
approaches ![]() , equals
, equals ![]() .
.
As implied from the way how limit is read, the limit of ![]() at
at ![]() equals
equals ![]() in fact means
in fact means
“the value of ![]() approaches
approaches ![]() , as
, as ![]() approaches
approaches ![]() .”
.”
Note on Nearness
It is critical to note ![]() is different from
is different from ![]() . In fact, for the limit of
. In fact, for the limit of ![]() to be defined,
to be defined, ![]() need only be defined near
need only be defined near ![]() , but not at
, but not at ![]() itself. Then, we might as well wonder what we mean by one value is near some other value, i.e. to what extent we might call one is near the other and from which point not near. This ambiguity around nearness will later be removed with the formal
itself. Then, we might as well wonder what we mean by one value is near some other value, i.e. to what extent we might call one is near the other and from which point not near. This ambiguity around nearness will later be removed with the formal ![]() –
–![]() definition of a limit, as well as with the concept of neighborhood.
definition of a limit, as well as with the concept of neighborhood.
Let us look at an example.
Example. Evaluate ![]()
Let ![]() .
.
We note that ![]() is defined on
is defined on ![]() , and thus
, and thus ![]() is not defined. Still, we can evaluate the limit of
is not defined. Still, we can evaluate the limit of ![]() at
at ![]() , since
, since ![]() is defined near 0. Let us have a look at the graph of
is defined near 0. Let us have a look at the graph of ![]() :
:
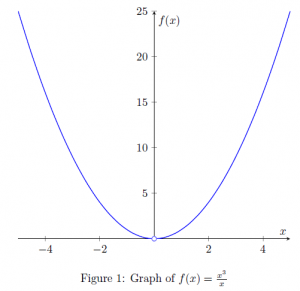
We observe ![]() approaches 0, as
approaches 0, as ![]() approaches 0 (Figure ??). Therefore,
approaches 0 (Figure ??). Therefore,
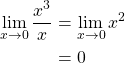
The cancellation of ![]() is valid, since
is valid, since ![]() by the definition of limit.
by the definition of limit.
Our discussion of limit so far has been on the intuitive definition that the value of the function ![]() approaches a certain value,
approaches a certain value, ![]() , as
, as ![]() approaches to the point where the limit is being evaluated,
approaches to the point where the limit is being evaluated, ![]() in our previous example. In fact, except where the limit is evaluated on the edge of a given interval, the value can be approached from both sides. That is, there are left-hand and right-hand limits. Let us examine the left-hand and right-hand limits at various points of a discontinuous function
in our previous example. In fact, except where the limit is evaluated on the edge of a given interval, the value can be approached from both sides. That is, there are left-hand and right-hand limits. Let us examine the left-hand and right-hand limits at various points of a discontinuous function ![]() defined by
defined by
![Rendered by QuickLaTeX.com \[ g(x)= \begin{cases} x^2 & (x<2) \\ x & (2\leq x <4) \\ -x+6 & (x\geq 4) \end{cases} \]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3b15e5c13c024eff12a0217a04393d0b_l3.png)
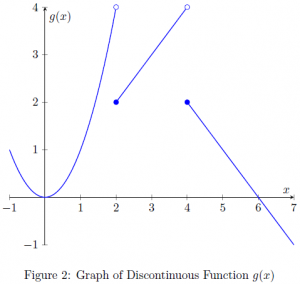
We observe ![]() , defined on
, defined on ![]() , is discontinuous at 2 points, at
, is discontinuous at 2 points, at ![]() and
and ![]() . In these cases, the limit is not defined, as the values near the point of interest, or the values of
. In these cases, the limit is not defined, as the values near the point of interest, or the values of ![]() approached from the left and from the right, are not the same. When we say approaching
approached from the left and from the right, are not the same. When we say approaching ![]() from the left and from the right, they correspond to inputting values of
from the left and from the right, they correspond to inputting values of ![]() , close to the point of interest, while less than and greater than, respectively.
, close to the point of interest, while less than and greater than, respectively.
While ![]() , when
, when ![]() is approached from the left around 2, the value approaches 4. In this case, we say, “the left-hand limit of
is approached from the left around 2, the value approaches 4. In this case, we say, “the left-hand limit of ![]() at 2 is 4,” and write
at 2 is 4,” and write
![]()
omitting 0 after the negative sign (![]() ). Note that the zero after the negative sign denotes an arbitrarily small, but positive, value but not equal to 0.
). Note that the zero after the negative sign denotes an arbitrarily small, but positive, value but not equal to 0.
Likewise, we can evaluate the right-hand limit of ![]() at 2 as the value of
at 2 as the value of ![]() near, but slightly greater than, 2, and write
near, but slightly greater than, 2, and write
![]()
Note that
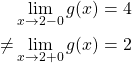
As above, in the cases where the values of the left-hand limit and the right-hand limit are not equal, we say the limit is not defined and divergent.
Let us discuss another divergent case, where the limit diverges to positive or negative infinity. One such function is ![]() . We know division by zero is not defined, and thus the domain of
. We know division by zero is not defined, and thus the domain of ![]() is non-zero real numbers, i.e.
is non-zero real numbers, i.e. ![]() . However,
. However, ![]() is defined on any number close to or near 0, no matter how small its absolute value is. Let us construct a table and observe a pattern:
is defined on any number close to or near 0, no matter how small its absolute value is. Let us construct a table and observe a pattern:
(1) ![]()
(2) ![]()
In the equation (2), we observe ![]() decreases and approaches 0 in the positive domain
decreases and approaches 0 in the positive domain ![]() , as the value of
, as the value of ![]() increases in
increases in ![]() towards infinity. When
towards infinity. When ![]() decreases in
decreases in ![]() and approaches 0, we see a rapid increase in
and approaches 0, we see a rapid increase in ![]() without a bound, i.e.
without a bound, i.e. ![]() .
.
The pattern found in the equation (1) is similar. A decrease in the magnitude of ![]() in the negative domain
in the negative domain ![]() results in the rapid increase in the magnitude of
results in the rapid increase in the magnitude of ![]() , which also is in
, which also is in ![]() . The absolute value of
. The absolute value of ![]() becomes smaller and approaches 0 in
becomes smaller and approaches 0 in ![]() with a decrease of
with a decrease of ![]() in
in ![]() .
.
The similar pattern observed in the equations (1) and (2) is owing to the fact ![]() is an odd function, i.e.
is an odd function, i.e. ![]() . We can see the symmetry about the origin in the plot (Figure 3).
. We can see the symmetry about the origin in the plot (Figure 3).
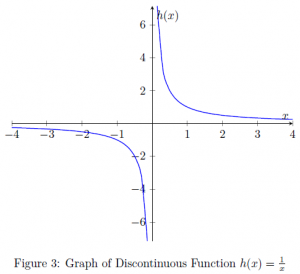
Following is the evaluation of limits at the singularities of ![]() , where
, where ![]() is not defined but the limit is defined:
is not defined but the limit is defined:
![Rendered by QuickLaTeX.com \[ \begin{cases} \lim_{x\to \infty} \frac{1}{x} &= 0\\ \lim_{x\to -\infty} \frac{1}{x} &= 0\\ \lim_{x\to 0^-} \frac{1}{x} &= -\infty\\ \lim_{x\to 0^+} \frac{1}{x} &= +\infty\\ \lim_{x\to 0} \frac{1}{x} &= \emptyset \end{cases}\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-dd90fd50c77cb6ecc51368e2d0d4f7f4_l3.png)
Note the limit of ![]() at
at ![]() is not defined.
is not defined.
Our discussion of left-hand and right-hand limits can be succinctly summarized as follows:
![]()
iff ![]() and
and ![]()
So far we have covered three cases as follows:
- The left-hand and right-hand limits are the same, and thus the limit at the point is defined; and the value of the function where the limit is evaluated is the same as the limit;
- Same as above, but the value of the function where the limit is evaluated is not defined or not equal to the limit; and
- The left-hand and right-hand limits are not the same.
Per case 1., the left-hand and right-hand limits are the same, and thus the limit at the point is defined; and the value of the function where the limit is evaluated is the same as the limit, we call the function is continuous at the evaluated point. Before moving onto the formal definition of a continuous function, precise definition of a limit is provided here.
Definition. (![]() –
–![]() Definition of Limit)
Definition of Limit)
Let ![]() be a function defined on some open interval that contains the number
be a function defined on some open interval that contains the number ![]() , except possibly at
, except possibly at ![]() itself. Then we say the limit of
itself. Then we say the limit of ![]() , as
, as ![]() approaches
approaches ![]() , is
, is ![]() , and we write
, and we write
![]()
if for every number ![]() there is a number
there is a number ![]() such that
such that
if ![]() , then
, then ![]() .
.
Above definition is commonly referred to as ![]() –
–![]() definition of a limit. With a bit of algebraic manipulation, the conditional inequalities can be equivalently expressed as follows:
definition of a limit. With a bit of algebraic manipulation, the conditional inequalities can be equivalently expressed as follows:
![]()
which translates to, “for any value of ![]() arbitrarily close to
arbitrarily close to ![]() , there exists
, there exists ![]() around
around ![]() , where the interval around
, where the interval around ![]() with a radius
with a radius ![]() is within the domain.”
is within the domain.”
Therefore, it follows that the substitution of antecedent with ![]() and
and ![]() corresponds to the
corresponds to the ![]() –
–![]() definition of the left-hand and the right-hand limits, respectively, since by forcing one of the interval endpoints around
definition of the left-hand and the right-hand limits, respectively, since by forcing one of the interval endpoints around ![]() to 0, approaching towards
to 0, approaching towards ![]() becomes one-sided.
becomes one-sided.
We recapitulate as follows
Definition. (![]() –
–![]() Definition of Left-Hand Limit)
Definition of Left-Hand Limit)
We write the left-hand limit of ![]() at
at ![]() is
is ![]() as
as
![]()
if for every number ![]() there is a number
there is a number ![]() such that
such that ![]() .
.
Definition. (![]() –
–![]() Definition of Right-Hand Limit)
Definition of Right-Hand Limit)
We write the right-hand limit of ![]() at
at ![]() is
is ![]() as
as
![]()
if for every number ![]() there is a number
there is a number ![]() such that
such that ![]() .
.
Let us illustrate the definition with an example.
Prove that ![]() .
.
1. Guessing a value for ![]() .
.
Let ![]() be given. We have to find a number
be given. We have to find a number ![]() such that
such that
![]()
Suppose ![]() , where
, where ![]() . Then,
. Then,
![]()
Then, we can make ![]() by letting
by letting ![]() , so we could choose
, so we could choose ![]() .
.
Let ![]() . Then,
. Then, ![]() , and thus
, and thus ![]() . Therefore, we have
. Therefore, we have ![]() , and so
, and so ![]() is a suitable choice for the constant.
is a suitable choice for the constant.
Then,
![]()
To ensure both inequalities above are satisfied, let ![]() .
.
2. Showing that this ![]() works.
works.
Let ![]() for
for ![]() .
.
If ![]() , then
, then
![Rendered by QuickLaTeX.com \[\begin{array}{cl} & |x-2|<1\\ \Rightarrow & 1<x<3\\ \Rightarrow & |x+2|<5 \text{ (as in part 1)} \end{array}\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-09b6c590c10b44b7f7abaae6bc625e74_l3.png)
Also, ![]() . Therefore,
. Therefore,
![]()
We have just shown, for every number ![]() , there is a number
, there is a number ![]() such that
such that ![]() . Therefore, by definition of
. Therefore, by definition of ![]() –
–![]() limit, we conclude
limit, we conclude ![]() .
.
Now we turn to continuity of a function. A continuous function is succinctly defined as
Definition. (Continuity)
A function ![]() is continuous at a number
is continuous at a number ![]() if
if
![]()
In fact, above definition implies the following:
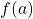 is defined (that is,
is defined (that is, 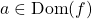 );
);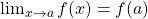 exists; and
exists; and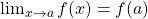
Likewise, it follows that
Definition. (Left- and Right-Continuity)
A function ![]() is continuous from the right at a number
is continuous from the right at a number ![]() if
if
![]()
and ![]() is continuous from the left at a number
is continuous from the left at a number ![]() if
if
![]()
So far we have only discussed the continuity of a function at a given point. In fact, the notion of continuity can be expanded to an interval, and we call this a continuous function. Following is a formal definition from Stewart [10]
Definition. (Continuous Function)
A function ![]() is continuous on an interval if it is continuous for all the numbers in the interval.
is continuous on an interval if it is continuous for all the numbers in the interval.
In this section, we began our discussion with an intuitive definition of a limit, and familiarized ourselves with limit through a few examples of left-hand and right-hand limits, and divergent cases. Then, we provided a refined and formal definition of a limit using ![]() and
and ![]() , and defined continuity of a function.
, and defined continuity of a function.
Now we are ready to discuss derivatives, the topic to be dealt in the following chapter, concerning the rate of change, where the prerequisite is a given function to be continuous. Let us delve in.
