20 Limits and Continuity
Again, we revisit limits and continuity. However, this time, we define the limit with a term, accumulation point, and focus on the limit of real-valued functions. Therefore, let us first define the accumulation point.
Definition. (Accumulation Point)
For a set ![]() , a point
, a point ![]() is an accumulation point of
is an accumulation point of ![]() if every deleted neighborhood of
if every deleted neighborhood of ![]() contains a point of
contains a point of ![]() .
.
The deleted neighborhood of ![]() refers to the neighborhood exclusive of the point of origin itself, i.e.
refers to the neighborhood exclusive of the point of origin itself, i.e.
![]()
Alternative terms for accumulation point are limit point or cluster point. Also, the accumulation point need not be in ![]() .
.
Definition. (Limit)
For an accumulation point ![]() of a set
of a set ![]() , given a mapping
, given a mapping ![]() , a real number
, a real number ![]() is a limit of
is a limit of ![]() , if for every
, if for every ![]() there exists
there exists ![]() such that
such that
![]()
Note that the notion of deleted neighborhood is inherent in ![]() , i.e.
, i.e. ![]() .
.
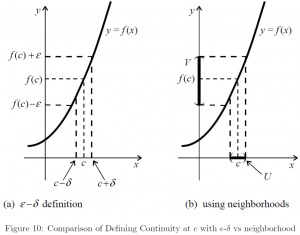
Formal definition of continuity at ![]() , provided in the calculus section, is obtained by requiring
, provided in the calculus section, is obtained by requiring ![]() and allowing for the possibility
and allowing for the possibility ![]() in the previous definition of a limit. Here we introduce another intuitive way of expressing the continuity using the notion of neighborhood.
in the previous definition of a limit. Here we introduce another intuitive way of expressing the continuity using the notion of neighborhood.
Theorem.
The statement ![]() of a mapping
of a mapping ![]() is continuous at
is continuous at ![]() is equivalent to
is equivalent to
for every neighborhood ![]() of
of ![]() , there exists a neighborhood
, there exists a neighborhood ![]() of
of ![]() such that
such that ![]() .
.
Note the equivalence of the two definitions [12]
One of most important properties of a continuous function is the intermediate value theorem.
Theorem. (Intermediate Value Theorem)
Given a continuous function ![]() , where
, where ![]() ,
,
the intermediate value theorem warrants the existence of ![]() such that
such that ![]() , where
, where ![]()
Let us illustrate with a straightforward example.
Example. Determine whether there is a root of ![]() on
on ![]() .
.
Let ![]() .
.
Then, ![]() and
and ![]() .
.
In fact, ![]() .
.
Therefore, by the intermediate value theorem, there exists at least one root of ![]() on
on ![]() .
.
Uniform Continuity
We conclude this section with uniform continuity, a different kind of continuity from an ordinary continuity. Formally, uniform continuity is defined as
Definition. (Uniform Continuity)
Given a function ![]() , the function
, the function ![]() is uniformly continuous on
is uniformly continuous on ![]() if for every
if for every ![]() there exists
there exists ![]() such that
such that
![]()
Roughly speaking, uniform continuity guarantees the proximity of the two values of the function, ![]() and
and ![]() , given the proximity of
, given the proximity of ![]() , whereas the maximum distance between
, whereas the maximum distance between ![]() and
and ![]() depends on
depends on ![]() themselves in ordinary continuous functions.
themselves in ordinary continuous functions.
Let us illustrate with an example.
Example. Examine whether ![]() is uniformly continuous.
is uniformly continuous.
![]()
Let ![]() .
.
If we let ![]() , then
, then ![]() .
.
Therefore, by letting ![]() , we can make
, we can make
![]()
Then, if we let ![]() and
and ![]() ,
,
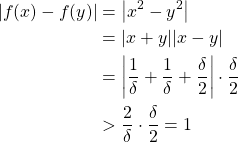
Therefore, ![]() is not uniformly continuous on
is not uniformly continuous on ![]() .
.
