9 Logic
Smith [14] says in the preface of his introductory textbook to advanced mathematics, “mathematics is concerned with the formation of a theory (collection of true statements) that describes patterns or relationships among quantities and structures.” To formulate a theory, we need logic, preferably a sound one, and among two lines of thoughts to build – deduction and induction. Let us begin with the definitions of a few key terms.
A proposition is a sentence that has one and only truth value, either true or false, usually denoted by T or F, respectively. The negation of a proposition ![]() , denoted by
, denoted by ![]() , is the proposition “not
, is the proposition “not ![]() .”
.”
Note that, colloquially, the negation and the denial of a proposition ![]() are essentially the same. However, in terms of logic, there is only one negation,
are essentially the same. However, in terms of logic, there is only one negation, ![]() , yet there can be many denials, so long as it is equivalent to the negation
, yet there can be many denials, so long as it is equivalent to the negation ![]() (e.g.
(e.g. ![]() ).
).
Continuing to introduce important terms, the conjunction of two propositions, denoted ![]() , means
, means ![]() and
and ![]() , whereas the disjunction of two propositions, denoted
, whereas the disjunction of two propositions, denoted ![]() , means
, means ![]() or
or ![]() . A tautology is a propositional form that is true, irrespective of the truth values of the propositions involved, and a contradiction, the opposite of a tautology, is a propositional form that is false, irrespective of the truth values of the propositions involved. In other words, tautology is always true and contradiction is always false.
. A tautology is a propositional form that is true, irrespective of the truth values of the propositions involved, and a contradiction, the opposite of a tautology, is a propositional form that is false, irrespective of the truth values of the propositions involved. In other words, tautology is always true and contradiction is always false.
Suppose there are ![]() propositions. Then, there can be
propositions. Then, there can be ![]() possible cases in total, since each proposition can be assigned either T or F, but not T and F. It would be convenient for us to list and examine all these possible cases in a structured way – it is a truth table. Looking at an example would make it easier to understand.
possible cases in total, since each proposition can be assigned either T or F, but not T and F. It would be convenient for us to list and examine all these possible cases in a structured way – it is a truth table. Looking at an example would make it easier to understand.
Example. Show that ![]() is a contradiction using a truth table.
is a contradiction using a truth table.
![Rendered by QuickLaTeX.com \[\begin{array}{ccc|ccc|c} P & Q & P \vee Q & \sim P & \sim Q & \sim P \, \wedge \sim Q & \left(P \vee Q\right)\wedge\left(\sim P \, \wedge \sim Q\right) \\ \hline T & T & T & F & F & F & F \\ F & T & T & T & F & F & F \\ T & F & T & F & T & F & F \\ F & F & F & T & T & T & F \end{array}\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-dfb5a6271e5e1266382ff9d6a92e86c8_l3.png)
The truth table above has 4 input rows, either T or F assigned to each proposition ![]() or
or ![]() . The proposition of interest,
. The proposition of interest, ![]() , is shown in the rightmost column. The columns in between reflect the steps we go through to evaluate the truth value of
, is shown in the rightmost column. The columns in between reflect the steps we go through to evaluate the truth value of ![]() , as the proposition is not in a form readily assessable.
, as the proposition is not in a form readily assessable.
In the first three columns, we assessed the truth value of the first half, ![]() , and in the three columns in the middle, the latter half,
, and in the three columns in the middle, the latter half, ![]() , then comparing the truth values of
, then comparing the truth values of ![]() and
and ![]() , we finally assign values to
, we finally assign values to ![]() in the last column. We can see, the values are all F, for all possible cases of
in the last column. We can see, the values are all F, for all possible cases of ![]() and
and ![]() . Therefore,
. Therefore, ![]() is a contradiction.
is a contradiction.
Definition. (The Equivalence of Propositional Forms)
The propositional forms having the same truth tables are equivalent.
What about conditional clauses? We all have heard of expressions in the form of, for example, “if ![]() , then
, then ![]() .” How do we deal with this? Let us define terms and introduce notations, first.
.” How do we deal with this? Let us define terms and introduce notations, first.
The conditional, denoted ![]() , means if
, means if ![]() , then
, then ![]() . The conditional in reverse order,
. The conditional in reverse order, ![]() , is called the converse and
, is called the converse and ![]() is called the contrapositive of
is called the contrapositive of ![]() . The biconditional, denoted
. The biconditional, denoted ![]() and read “
and read “![]() if and only if (iff)
if and only if (iff) ![]() “, means the truth value of
“, means the truth value of ![]() and
and ![]() are always the same.
are always the same.
Utilizing the conditionals, here we introduce a famous theorem:
Theorem.
For propositions ![]() and
and ![]() ,
,
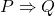 is equivalent to
is equivalent to 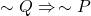
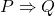 is not equivalent to
is not equivalent to 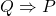
Proof.
The proof is straightforward with a truth table. Note the truth value of ![]() is identical with
is identical with ![]() , but not with
, but not with ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{ccc|ccc|c} P & Q & P \Rightarrow Q & \sim Q & \sim P & \sim Q \Rightarrow \,\sim P & Q \Rightarrow P \\ \hline T & T & T & F & F & T & T \\ F & T & T & F & T & T & F \\ T & F & F & T & F & F & T \\ F & F & T & T & T & T & T \end{array}\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f126d91bb56d963e6b094d5aa29646e5_l3.png)
Note that, by the Hierarchy of Connectives, the connectives are always applied in the order of ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
DeMorgan’s Laws
Now we introduce famous DeMorgan’s Laws. On hearing DeMorgan’s Laws, Some might recall a set theory. However, originally DeMorgan’s Laws were established in propositional logic and Boolean algebra.
Theorem. (DeMorgan’s Laws)
For propositions ![]() and
and ![]() ,
,
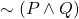 is equivalent to
is equivalent to 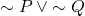
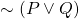 is equivalent to
is equivalent to 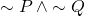
Proof of DeMorgan’s Laws.
Following are the truth tables of cases of DeMorgan’s Laws.
![Rendered by QuickLaTeX.com \[\begin{array}{ccc|c|ccc} P & Q & P \wedge Q & \sim(P \wedge Q) & \sim P & \sim Q & \sim P \, \vee \sim Q \\ \hline T & T & T & F & F & F & F \\ T & F & F & T & F & T & T \\ F & T & F & T & T & F & T \\ F & F & F & T & T & T & T \\ \end{array}\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a148df546456b668410580dd028b3461_l3.png)
We can see the equivalence of ![]() and
and ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{ccc|c|ccc} P & Q & P \vee Q & \sim(P \vee Q) & \sim P & \sim Q & \sim P \, \wedge \sim Q \\ \hline T & T & T & F & F & F & F \\ T & F & T & F & F & T & F \\ F & T & T & F & T & F & F \\ F & F & F & T & T & T & T \\ \end{array}\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1f84fb7804e8f602e5fb234ed7b29c83_l3.png)
We can see the equivalence of ![]() and
and ![]() .
.
We see a pattern, when removing a parenthesis, ![]() is applied to and flips each element inside, converting
is applied to and flips each element inside, converting ![]() to
to ![]() ,
, ![]() to
to ![]() , and vice versa.
, and vice versa.
