30 One-Variable Equation
In this section, we deal with equations with only a single variable, most often denoted by ![]() , either polynomial, non-linear, or mixed functions.
, either polynomial, non-linear, or mixed functions.
The Bisection Method
The bisection method is arguably the most basic and elementary analytic approach to obtaining solutions. In fact, this is based on the intermediate value theorem discussed in the previous section Analysis, specifically, limits and continuity.
Let us revisit the intermediate value theorem.
Intermediate Value Theorem
Given a continuous function ![]() , where
, where ![]() , the intermediate value theorem} warrants the existence of at least one solution in
, the intermediate value theorem} warrants the existence of at least one solution in ![]() such that
such that ![]() , where
, where ![]() .
.
Here, we let ![]() . Then, the intermediate value theorem becomes
. Then, the intermediate value theorem becomes ![]() . Let us illustrate the iteration algorithm of bisection method with the second motivating example where
. Let us illustrate the iteration algorithm of bisection method with the second motivating example where ![]() .
.
1. Identify 2 points ![]() and
and ![]() such that
such that ![]() and
and ![]() .
.
![]()
Therefore, let ![]() .
.
Arbitrarily, let us check ![]() .
.
![]()
Therefore, let ![]() .
.
2. Set the first midpoint ![]() .
.
Then, ![]() .
.
Therefore,
![]()
Therefore, let ![]() , and keep
, and keep ![]() .
.
3. Continue iteration with ![]() .
.
- if
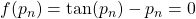 , then we are done with a conclusion
, then we are done with a conclusion 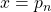 .
. - if
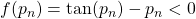 , then let
, then let 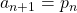 and
and  , and continue iteration.
, and continue iteration. - if
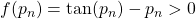 , then let
, then let 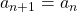 and
and 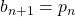 , and continue iteration.
, and continue iteration.
4. Terminate when one of the stopping criteria is met:
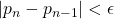
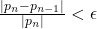 , where
, where 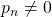
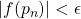
where ![]() is some small number we set (e.g.
is some small number we set (e.g. ![]() ).
).
Stopping Criterion
There is no right or wrong criteria for stopping. Rather, it actually depends on how much we know about the behavior of ![]() and
and ![]() . However, if little is known about
. However, if little is known about ![]() and
and ![]() , then we would be better off by taking the safest or the most conservative approach, (b)
, then we would be better off by taking the safest or the most conservative approach, (b) ![]() , where
, where ![]() , since this criterion is closest to testing relative error.[7]
, since this criterion is closest to testing relative error.[7]
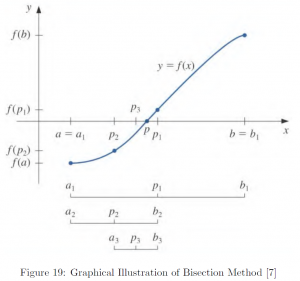
Let us have a look how first ten iterations look. Errors in the last column were defined as ![]() , where
, where ![]() , a reasonably accurate estimate of
, a reasonably accurate estimate of ![]() , was assumed to be the solution of
, was assumed to be the solution of ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{c|ccccccc} n &a_n &b_n &f(a_n) &f(b_n) & p_n & f(p_n) & \text{Error} \\ \hline 1 &4.4 &4.5 &-1.3037 &0.1373 &4.45 &-0.7267 &0.043410\\ 2 &4.45 &4.5 &-0.7267 &0.1373 &4.475 &-0.3419 &0.018410\\ 3 &4.475 &4.5 &-0.3419 &0.1373 &4.4875 &-0.1161 &0.005910\\ 4 &4.4875 &4.5 &-0.1161 &0.1373 &4.4938 &0.0069 &0.000341\\ 5 &4.4875 &4.4938 &-0.1161 &0.0069 &4.4906 &-0.0555 &0.002784\\ 6 &4.4906 &4.4938 &-0.0555 &0.0069 &4.4922 &-0.0245 &0.001222\\ 7 &4.4922 &4.4938 &-0.0245 &0.0069 &4.4930 &-0.0089 &0.000441\\ 8 &4.4930 &4.4938 &-0.0089 &0.0069 &4.4934 &-0.0010 &0.000050\\ 9 &4.4934 &4.4938 &-0.0010 &0.0069 &4.4936 &0.0029 &0.000145\\ 10 &4.4934 &4.4934 &-0.0010 &0.0029 &4.4935 &0.0010 &0.000048 \end{array} \]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c5546902d98c6691ced7952cd3b1cc94_l3.png)
We observe a decreasing trend in errors, yet note it only is a trend, but not absolute. In fact, the errors have increased from eighth through tenth iterations, though minimally.
Newton’s Method
Now we turn to the famous Newton’s or Newton-Rhapson method, based on Taylor’s theorem. Owing to its utility and power, naturally this technique has become well-known.
Let us first have a look at Taylor’s theorem.
Theorem. (Taylor’s Theorem [7])
Suppose ![]() is a
is a ![]() -differentiable function
-differentiable function ![]() , denoted
, denoted ![]() ;
; ![]() is defined on
is defined on ![]() ; and
; and ![]() . Then, for all
. Then, for all ![]() , there exists a number
, there exists a number ![]() between
between ![]() and
and ![]() with
with
![]()
where
![]()
and
![]()
In Taylor’s theorem, ![]() is decomposed into two different functions
is decomposed into two different functions ![]() and
and ![]() , which denote the
, which denote the ![]() -th Taylor polynomial and the remainder term (or truncation error), respectively. By taking
-th Taylor polynomial and the remainder term (or truncation error), respectively. By taking ![]() to the limit, we obtain the famous Taylor series and the special case where
to the limit, we obtain the famous Taylor series and the special case where ![]() is called a Maclaurin series.
is called a Maclaurin series.
Note that Taylor’s theorem only ensures the existence of some number ![]() in the interval
in the interval ![]() , but does not guarantee explicit determination of
, but does not guarantee explicit determination of ![]() . Still, the warranted existence of
. Still, the warranted existence of ![]() allows us to conduct an error analysis and determine an error bound.
allows us to conduct an error analysis and determine an error bound.
To derive Newton’s method, let us consider the Taylor expansion of ![]() expanded about
expanded about ![]() and evaluated at
and evaluated at ![]() :
:
![]()
Let ![]() , i.e.
, i.e. ![]() is the solution of our interest. Then,
is the solution of our interest. Then,
![]()
It is our assumption ![]() is small. Therefore, higher powers of
is small. Therefore, higher powers of ![]() would be even smaller. Hence,
would be even smaller. Hence,
![]()
Solving for ![]() , we have
, we have
![]()
Generalizing for ![]() iteration,
iteration,
![]()
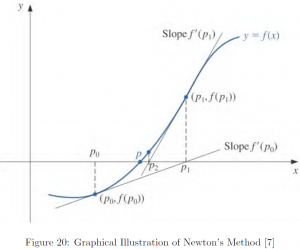
Let us illustrate with an example, where ![]() . Following is the tabulated result of first four iterations. As in the case of the previous example, errors were defined as
. Following is the tabulated result of first four iterations. As in the case of the previous example, errors were defined as ![]() at
at ![]() , a reasonably accurate estimate of
, a reasonably accurate estimate of ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{c|cccc} n & p_n & f(p_n) & f'(p_n) & \text{Error} \\ \hline 0 & 4.5\quad\quad\:\, & 0.137332 & 21.504849 & 0.006591 \\ 1 & 4.493614 & 0.004132 & 20.229717 & 0.000204 \\ 2 & 4.493410 & 0.000004 & 20.190766 & 0.000000 \\ 3 & 4.493409 & 0.000000 & 20.190729 & 0.000000 \\ 4 & 4.493409 & 0.000000 & 20.190729 & 0.000000 \end{array} \]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a88039cc42533b68924f7cb94455c907_l3.png)
Note that how rapidly the error decreases below ![]() with only two iterations. One might as well think this might be a coincidence. Therefore, let us run another iteration with
with only two iterations. One might as well think this might be a coincidence. Therefore, let us run another iteration with ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{c|cccc} n & p_n & f(p_n) & f'(p_n) & \text{Error} \\ \hline 0 &4.600000 &4.260175 &78.502699 &0.106591\\ 1 &4.545732 &1.398966 &35.339431 &0.052323\\ 2 &4.506146 &0.273551 &22.845500 &0.012736\\ 3 &4.494172 &0.015444 &20.336636 &0.000762\\ 4 &4.493412 &0.000055 &20.191250 &0.000003\\ 5 &4.493409 &0.000000 &20.190729 &0.000000 \end{array} \]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-82229d676c1c160086afe98f3f18f0f8_l3.png)
Again, note the rapid reduction in errors. With only five iterations the error went below ![]() . In fact, this efficiency in approximation is the basis of the fame and wide applications of the Newton’s method. Comparing with the bisection method based on the same initial value
. In fact, this efficiency in approximation is the basis of the fame and wide applications of the Newton’s method. Comparing with the bisection method based on the same initial value ![]() , where merely a fair at best estimate with an error only under
, where merely a fair at best estimate with an error only under ![]() was obtained after ten iterations, the Newton’s method yielded much more accurate estimate with an error under
was obtained after ten iterations, the Newton’s method yielded much more accurate estimate with an error under ![]() with only two iterations.
with only two iterations.
So, can we say the Newton’s method has dominance over the bisection method? The answer is no. While the Newton’s method is substantially powerful with many strengths, it is not universally applicable. To begin with, the main limitation of the Newton’s method is ![]() has to be defined, i.e. the function of interest
has to be defined, i.e. the function of interest ![]() has to be differentiable, yet this is not always the case for a continuous function
has to be differentiable, yet this is not always the case for a continuous function ![]() .
.
