Probabilistic Model

Donovan D Chang

35 Probabilistic Model

Now we turn our attention to a probabilistic or stochastic model as opposed to a deterministic model. In other words, there was no randomness involved in our previous discussion of models. In this section, we shall consider a stochastic process named Marcov chain, where a equilibrium is reached after a long period of time. Following is a motivating example.

Example. Suppose a town in oligopoly with only two cleaners A and B. Therefore, each household has 3 choices: be a patron of cleaner A, or of cleaner B, or do it by himself (denoted by option C). Each month, the residents change their shop or shift their behavior according to the probabilities arranged in the transition table below:

$\begin{array}{c|ccc} & A' & B' & C' \\ \hline A & 0.2 & 0.4 & 0.4 \\ B & 0.6 & 0.1 & 0.3 \\ C & 0.5 & 0.2 & 0.3 \end{array}$

For example, among those who were a patron of cleaner A in month 1, only 20% will continue to be a patron in month 2; but 40% will use cleaner B; and the rest, 40%, will take care of their laundry within their household.

Assuming this transition pattern persists, compute the proportion of each population A, B, and C in equilibrium in the long run.

There are two approaches to this problem. One is using the notion of a limit, as the problem states in the long run it reaches an equilibrium after enough time passes. The other is taking the probabilistic modeling approach.

1. Using the Limit
Let $a_n$ , $b_n$ , and $c_n$ , denote the proportion of utilizing options A, B, and C, respectively, in month $n$ . Then,

$\begin{align*} a_{n+1} &= 0.2a_n + 0.6b_n + 0.5c_n\\ b_{n+1} &= 0.4a_n + 0.1b_n + 0.2c_n\\ c_{n+1} &= 0.4a_n + 0.3b_n + 0.3c_n \end{align*}$

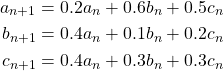
Since the limit exists, we can let

$\begin{align*} \lim_{n\rightarrow\infty} a_{n+1} &= \lim_{n\rightarrow\infty} a_n = a\\ \lim_{n\rightarrow\infty} b_{n+1} &= \lim_{n\rightarrow\infty} b_n = b\\ \lim_{n\rightarrow\infty} c_{n+1} &= \lim_{n\rightarrow\infty} c_n = c \end{align*}$

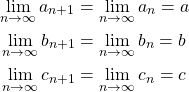
Then, the above linear system becomes

$\begin{align*} a &= 0.2a + 0.6b + 0.5c\\ b &= 0.4a + 0.1b + 0.2c\\ c &= 0.4a + 0.3b + 0.3c \end{align*}$

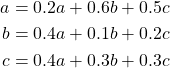
Then, this amounts to solving for 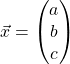$\vec{x}=\begin{pmatrix} a\\b\\c \end{pmatrix}$ given by

$\begin{pmatrix} -0.8 &0.6 &0.5\\ 0.4 &-0.9 &0.2\\ 0.4 &0.3 &-0.7 \end{pmatrix} \vec{x} =\vec{0}$

Then,

$\vec{x}=\begin{pmatrix} a\\b\\c \end{pmatrix} =\begin{pmatrix} 40.43\\25.53\\34.04 \end{pmatrix}$

2. Probabilistic Modeling Approach
Again, we begin from the set of equations

$\begin{align*} a_{n+1} &= 0.2a_n + 0.6b_n + 0.5c_n\\ b_{n+1} &= 0.4a_n + 0.1b_n + 0.2c_n\\ c_{n+1} &= 0.4a_n + 0.3b_n + 0.3c_n \end{align*}$

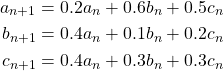
However, this time, instead of taking the limit of the equations above, we run a simulation. As it was stated in the problem the equilibrium exists, the values at the beginning, i.e. $a_1,b_1,$ and $c_1$ are irrelevant, so long as they meet the following conditions:

$a_1+b_1+c_1=1$
$a_1,b_1,c_1\geq 0$

Therefore, we arbitrarily assign $a_1=1$ and $b_1=c_1=0$ . Following is the result of a few rounds of simulation:

$\begin{array}{c|ccc} n &a_n &b_n &c_n\\ \hline 1 &1 &0 &0\\ 2 &0.2 &0.4 &0.4\\ 3 &0.48 &0.2 &0.32\\ 4 &0.376 &0.276 &0.348\\ 5 &0.4148 &0.2476 &0.3376\\ 6 &0.4003 &0.2582 &0.3415\\ 7 &0.4057 &0.2542 &0.3400\\ 8 &0.4037 &0.2557 &0.3406\\ 9 &0.4045 &0.2552 &0.3404\\ 10 &0.4042 &0.2554 &0.3404\\ 11 &0.4043 &0.2553 &0.3404\\ 12 &0.4042 &0.2553 &0.3404\\ 13 &0.4043 &0.2553 &0.3404\\ 14 &0.4043 &0.2553 &0.3404\\ 15 &0.4043 &0.2553 &0.3404 \end{array}$

Table 1. First 15 Iterations with $a_1=1$ and $b_1=c_1=0$

We can see an equilibrium of $a_n=0.4043,b_n=0.2553,$ and $c_n=0.3404$ is reached from the 13th month after 12 iterations.

Let us examine whether the equilibrium is reached early when different initial values of $a_1,b_1,$ and $c_1$ are assigned. This time, we assign $a_1=b_1=0.3$ and $c_1=0.4$ .

$\begin{array}{c|ccc} n &a_n &b_n &c_n\\ \hline 1 &0.3 &0.3 &0.4\\ 2 &0.44 &0.23 &0.33\\ 3 &0.391 &0.265 &0.344\\ 4 &0.4092 &0.2517 &0.3391\\ 5 &0.4024 &0.2567 &0.3409\\ 6 &0.4049 &0.2548 &0.3402\\ 7 &0.4040 &0.2555 &0.3405\\ 8 &0.4044 &0.2552 &0.3404\\ 9 &0.4042 &0.2553 &0.3404\\ 10 &0.4043 &0.2553 &0.3404\\ 11 &0.4043 &0.2553 &0.3404\\ 12 &0.4043 &0.2553 &0.3404\\ 13 &0.4043 &0.2553 &0.3404\\ 14 &0.4043 &0.2553 &0.3404\\ 15 &0.4043 &0.2553 &0.3404 \end{array}$

Table 2. First 15 Iterations with $a_1=b_1=0.3$ and $c_1=0.4$

This time, the same equilibrium, $a_n=0.4043,b_n=0.2553,$ and $c_n=0.3404$ , is reached after only 9 iterations from 10th month. As we expected, reaching the same equilibrium is a matter of time, not a matter of initial values assigned to $a_1,b_1,$ and $c_1$ .

35 Probabilistic Model

License

Share This Book