10 Proof Techniques
So far we have seen the power and utility of a truth table. However, it might be inconvenient and even inefficient to lay out all possible cases every time we attempt to prove certain claims. Thus there is a need for theorems, rules, and techniques to save time as well as organize our ideas.
The modus ponens rule is the most fundamental rule of our deductive reasoning, based on the tautology
![]()
In other words, whenever we have ![]() and
and ![]() , then we can conclude
, then we can conclude ![]() is true.
is true.
The details of such techniques are mentioned in the following subsections.
Direct Proofs
The structure of direct proof [14] of ![]() is simple, and takes the following form:
is simple, and takes the following form:
Direct Proof.
Assume ![]() .
.
![]()
Therefore, ![]() .
.
Therefore, ![]() .
.
Let us clarify with an example.
Example. Prove if ![]() is even, then
is even, then ![]() is odd.
is odd.
Proof.
Let ![]() be an even integer.
be an even integer.
Then, there exists ![]() such that
such that ![]() .
.
Then, ![]() .
.
Therefore, ![]() is odd for all
is odd for all ![]() .
.
Therefore, if ![]() is even, then
is even, then ![]() is odd.
is odd.
Above is the typical example of a direct proof – we began with the assumption
![]() :
: ![]() is even
is even
and with an elementary arithmetic operation we deduced
![]() :
: ![]() is even
is even
Indeed, this is quite simple an example, but illustrative of the direct proof method. Let us have a look at another.
Example. Let ![]() . Prove that if
. Prove that if ![]() , then
, then ![]()
Proof.
Let ![]() .
.
Then, ![]() and
and ![]() .
.
Therefore, ![]() .
.
Therefore, ![]() , where
, where ![]() .
.
Therefore, if ![]() , then
, then ![]() .
.
To analyze, again, we began with the assumption
![]()
and with an elementary arithmetic operation we deduced
![]() and thus
and thus ![]()
Contraposition
Reasoning with the contrapositive or contraposition is also a well-known proof technique. Let us revisit the theorem of contraposition.
![]()
The proof by contrapositive takes the following form:
Proof by Contrapositive/Contraposition.
Assume ![]() .
.
![]()
Therefore, ![]() .
.
Therefore, ![]() .
.
If and only if ![]() .
.
Let us illustrate with examples.
Example. Prove that if ![]() is odd, then
is odd, then ![]() is odd.
is odd.
Following our usual strategy, we might as well begin our proof by denoting an odd number ![]() for
for ![]() . However, this form does not really help, and we are not really sure how to proceed to show
. However, this form does not really help, and we are not really sure how to proceed to show ![]() is odd.
is odd.
Instead, the consequent that ![]() is odd, and the converse of the consequent that
is odd, and the converse of the consequent that ![]() is even, fit the format we usually denote an odd/even number. Therefore, we strategize to prove the contrapositive, i.e. if
is even, fit the format we usually denote an odd/even number. Therefore, we strategize to prove the contrapositive, i.e. if ![]() is even, then
is even, then ![]() is even.
is even.
Proof.
Suppose ![]() is even.
is even.
That is, there exists ![]() such that
such that ![]() .
.
Then,
![]()
Therefore, ![]() is even for all
is even for all ![]() .
.
Therefore, if ![]() is even, then
is even, then ![]() is even.
is even.
Therefore, if ![]() is odd, then
is odd, then ![]() is odd.
is odd.
Indirect Proofs
Indirect proofs are proofs based on tautologies, the statements that are always true, irrespective of the truth values of the propositions involved. Proof by contraposition was a motivating example of indirect proofs. In this section, we introduce another indirect proof technique, proof by contradiction. Following is the typical form of proof by contradiction:
Proof by Contradiction.
Assume ![]() .
.
![]()
Therefore, ![]() .
.
![]()
Also, ![]() .
.
This is contradiction, both ![]() and
and ![]() cannot be true at the same time. And therefore, we conclude it must be the case our assumption was wrong, i.e.
cannot be true at the same time. And therefore, we conclude it must be the case our assumption was wrong, i.e. ![]() , equivalent to
, equivalent to ![]() , equivalent to
, equivalent to ![]() , is true.
, is true.
Let us illustrate with an example.
Example. Prove ![]() is irrational.
is irrational.
Our proof is divided into several parts. To prove by contradiction, first, we shall assume the negation, ![]() is not irrational, and thus rational. Then, we express this “rational number” as a fraction. While proceeding, we shall inevitably face a contradiction, since our assumption
is not irrational, and thus rational. Then, we express this “rational number” as a fraction. While proceeding, we shall inevitably face a contradiction, since our assumption ![]() is rational is incorrect.
is rational is incorrect.
Proof.
First, assume the converse is true.
Suppose ![]() is rational.
is rational.
Then, there exist integers ![]() such that
such that ![]() , where
, where ![]() and
and ![]() .
.
Then,
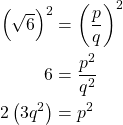
Therefore, ![]() is even.
is even.
Show ![]() is even
is even ![]()
![]() is even
is even
This part, let us prove the contrapositive.
Suppose ![]() is odd.
is odd.
Then, there exists ![]() such that
such that ![]() .
.
Then,
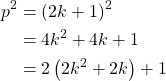
Therefore, ![]() is odd for all
is odd for all ![]() .
.
Therefore, if ![]() is odd, then
is odd, then ![]() is odd.
is odd.
Then, if ![]() is even, then
is even, then ![]() is even.
is even.
Finally, show ![]() is even
is even ![]()
![]() is even
is even ![]()
![]() is even.
is even.

Therefore, ![]() is even.
is even.
Then, likewise, ![]() is even.
is even.
In fact, it was our part of assumption ![]() . However, since both
. However, since both ![]() and
and ![]() are even
are even ![]() . This is contradiction – it must be the case our assumption was wrong, i.e.
. This is contradiction – it must be the case our assumption was wrong, i.e. ![]() is not rational, and thus irrational. Therefore, we conclude
is not rational, and thus irrational. Therefore, we conclude ![]() is irrational.
is irrational.
Proof by Exhaustion
Proof by exhaustion is a technique to examine every possible case. Let us illustrate with an example.
Example. Prove ![]() for
for ![]() .
.
Proof.
1. ![]() and
and ![]()
Then, ![]() ,
, ![]() , and
, and ![]() .
.
Therefore, ![]() .
.
2. ![]() and
and ![]()
Then, ![]() ,
, ![]() , and
, and ![]() .
.
Therefore, ![]() .
.
3. ![]() and
and ![]()
Then, ![]() ,
, ![]() , and
, and ![]() .
.
Therefore, ![]() .
.
4. ![]() and
and ![]()
Then, ![]() ,
, ![]() , and
, and ![]() .
.
Therefore, ![]() .
.
Therefore, ![]() for
for ![]() .
.
Mathematical Induction
Our discussion so far has been focused on deductive reasoning. Yes, deduction is our primary method of unfolding our logic, yet we also have briefly mentioned the existence of the principles of mathematical induction (PMI). Following is the basic scheme of the proof using the PMI:
Proof using the Principles of Mathematical Induction.
Let ![]() for
for ![]() be the collection of propositions.
be the collection of propositions.
1. (Basis Step) Show that ![]() is true.
is true.
2. (Inductive Step) Show that, for all ![]() , if
, if ![]() is true, then
is true, then ![]() is true.
is true.
3. Therefore, we conclude ![]() is true for all
is true for all ![]() by the principles of mathematical induction.
by the principles of mathematical induction.
Let us illustrate with a famous example, well-known as the problem of the Tower of Hanoi.
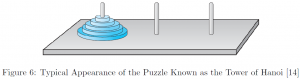
Example. The Tower of Hanoi
The Tower of Hanoi, also called the Tower of Brahma or Lucas’ Tower, is a famous mathematical puzzle. It is consisted of 3 rods and ![]() number of disks with differing radii (Figure ??). At the initial state, the disks are placed in a single rod with diameters increasing from top to bottom. The goal is to move the disks to another rod in the same order with the following rules:
number of disks with differing radii (Figure ??). At the initial state, the disks are placed in a single rod with diameters increasing from top to bottom. The goal is to move the disks to another rod in the same order with the following rules:
1. Only one disk at the top of the rod can be moved to another rod in each turn.
2. Larger disk cannot be placed on top of a smaller disk.
It is known the fewest number of movements to solve the puzzle is ![]() . Prove this using the PMI.
. Prove this using the PMI.
Proof of the Tower of Hanoi.
1. (Basis Step) Show that ![]() is true.
is true.
Let ![]() .
.
Then, ![]() is true, since we only need a single movement to migrate a single piece of disk.
is true, since we only need a single movement to migrate a single piece of disk.
2. (Inductive Step) Show that, for all ![]() , if
, if ![]() is true, then
is true, then ![]() is true.
is true.
Suppose ![]() .
.
Then, to completely migrate a stack of ![]() pieces placed in one rod, we first need to move
pieces placed in one rod, we first need to move ![]() pieces from the top, except the last piece; move the last piece; and then on top of the last piece place the first
pieces from the top, except the last piece; move the last piece; and then on top of the last piece place the first ![]() pieces that were moved. Therefore,
pieces that were moved. Therefore,
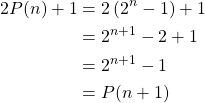
Therefore the statement, the puzzle with ![]() disks can be solved in
disks can be solved in ![]() moves, is true for
moves, is true for ![]() .
.
3. Therefore, we conclude ![]() is true for all
is true for all ![]() by the principles of mathematical induction.
by the principles of mathematical induction.
