Relations

Donovan D Chang

13 Relations

Relations

Now that we have studied sets, we begin to relate elements in sets. The elements can be related between across multiple or between different sets, as well as linked on its own. In all cases are called relations. To define a relation from set $A$ to set $B$ , the concept of cartesian product or cross product is needed. Let us explore.

Definition. (Cartesian/Cross Product)
Let $A$ and $B$ be sets. The cartesian product or cross product of $A$ and $B$ is

$A\times B=\left\lbrace (a,b):a\in A \, \text{and}\,b\in B \right\rbrace$

Definition. (Relation)
Let $A$ and $B$ be sets. The relation from $A$ to $B$ is defined as a subset of $A \times B$ . To denote $a$ is $R$ -related or related to $b$ , we write

$(a,b)\in R\Leftrightarrow a \, R \, b$

Suppose there is a relation from $A$ to $B$ , where $A$ and $B$ are nonempty sets. As $a \, R \, b$ is defined as a subset of $A \times B$ , considering all subsets, not all elements have to be related. In other words, there will be some elements related in $A$ , as well as in $B$ . Formally, they are defined as

Definition. (Domain and Range)
The domain of the relation $R$ from $A$ to $B$ is the set

$Dom(R) = \left\lbrace x\in A: \text{there exists } y\in B \text{ such that } x\,R\,y\right\rbrace$

The range of the relation $R$ from $A$ to $B$ is the set

$Rng(R) = \left\lbrace y\in B: \text{there exists } x\in A \text{ such that } x\,R\,y\right\rbrace$

Note that by definition, $Dom(R)\subseteq A$ and $Rng(R)\subseteq B$ .

Now, let us consider some special cases. A relation can also be defined from set $A$ to $A$ itself. If so, it is called a relation on $A$ . Further, if each element $a$ of $A$ is related to the same element $a$ itself, it is called the identity relation on $A$ , and denoted

$I_A = \left\lbrace (x,x): x\in A\right\rbrace$

Also, we can define the relation, the inverse of $R$ , whose element pairs are reversed, i.e.

$R^{-1} = \left\lbrace (y,x):(x,y)\in R \right\rbrace$

Naturally, the following theorem is borne.

Theorem.
For any relation $R$ from $A$ to $B$ ,
* $Dom \left( R^{-1}\right) = Rng(R)$
* $Rng \left( R^{-1}\right) = Dom(R)$

We can also consider a relation where multiple sets are involved. For example, when $R$ is a relation from $A$ to $B$ , and $S$ is a relation from $B$ to $C$ , the composite of $R$ and $S$ is

$S\circ R = \left\lbrace (a,c):\text{there exists } b\in B \text{ such that }(a,b)\in R \text{ and } (b,c)\in S \right\rbrace$

Note that the order of the composite is from right to left, not from left to right.

Some useful theorems are as follows:

Theorem.
* $\left( R^{-1} \right) = R$
* $T\circ (S\circ R) = (T\circ S) \circ R$
i.e. composition of relations is associative.
* $\left( S\circ R\right)^{-1} = R^{-1} \circ S^{-1}$

We conclude this chapter with some examples.

In fact, the familiar linear function $y=f(x)=x$ , with slope $1$ , can be viewed as the identity relation $f$ of $\mathbb{R}$ on $\mathbb{R}$ . Indeed, $Dom(f) = Rng(f) = \mathbb{R}$ .

Let $f$ be the relation on $\mathbb{R}^+$ given by $x\,f\,y$ iff $y=\ln x$ .
Then, the inverse of $f$ is obtained by switching $x$ and $y$ , i.e.

$x\,f\,y \text{ iff } x = \ln y$

Then,

$y = e^x$

Note that $Dom(f) = Rng\left(f^{-1}\right) = \mathbb{R}^+$ and
$Rng(f) = Dom\left(f^{-1}\right) = \mathbb{R}$ .

Equivalence Relations

While exploring relations, we can discover a few traits of relations, namely, reflexivity, symmetry, and transitivity. We define an equivalence relation as a relation that is reflexive, symmetric, and transitive. Let us examine each trait as follows.

Definition. (Equivalence Relation)
A relation $R$ on $A$ is an equivalence relation with the following attributes:

1. Reflexivity
$(x,x)\in R$ for all $x\in A$ .

2. Symmetry
$(x,y)\in R\Rightarrow (y,x)\in R$ for all $x,y\in A$ .

3. Transitivity
$(x,y),(y,z)\in R \Rightarrow (x,z)\in R$ for all $x,y,z\in A$ .

Let us illustrate with an example.

Example. Determine whether $R$ given by “ $=$ ” on $\mathbb{N}$ is an equivalence relation.

Let $R$ given by “ $=$ ” be a relation on $\mathbb{N}$ .
Then, this relation is in fact $I_{\mathbb{N}}$ , and thus an equivalence relation. To verify,

1. Reflexivity
$(n,n)\in R$ for all $n\in \mathbb{N}$ .

2. Symmetry
In fact, $(n,n)$ is the only form found in $R$ , i.e. there does not exist $(a,b)\in R$ such that $a\neq b$ .
Therefore, $R$ is symmetric, since $(n,n)\in R$ for all $n\in \mathbb{N}$ .

3. Transitivity
Again, since $(n,n)$ is the only form found in $R$ , $R$ is transitive.

In fact, the concept of an equivalence relation entails another important concept, the equivalence class, partitioning the set into disjoint sets.

Definition. (Equivalence Relation and Equivalence Class)
Let $R$ be an equivalence relation on a set $A$ . Then, the equivalence class of $x\in A$ determined by $R$ is

$x/R=\bar{x}=[x]=\left\lbrace y\in A:x\,R\,y \right\rbrace$

with alternative names of “the class of $x$ modulo $R$ ” or “ $x$ mod $R$ “.
The set of all equivalence classes of $A$ over $R$ is called $A$ modulo $R$ , denoted

$A/R = \left\lbrace x/R:x\in A\right\rbrace$

Let us illustrate with an example.

Example. Identify all equivalence classes of the relation

$H=\left\lbrace (0,0),(1,1),(2,2),(3,3),(1,2),(2,1) \right\rbrace$

on the set $A=\left\lbrace 0,1,2,3\right\rbrace$ .

Note

$\begin{align*} 0/H &= \left\lbrace 0\right\rbrace\\ 1/H = 2/H &= \left\lbrace 1,2 \right\rbrace\\ 3/H &= \left\lbrace 3 \right\rbrace \end{align*}$

Therefore,

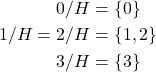
$A/H = \left\lbrace \left\lbrace 0\right\rbrace,\left\lbrace 1,2 \right\rbrace, \left\lbrace 3 \right\rbrace \right\rbrace$

We can see each element of $A/H$ is mutually disjoint and thus partitions the original set $A$ .

Ordering Relations

So far we have discussed sets and set theory; and building a relation by linking elements across sets. Now we turn our focus to the order or hierarchy of elements contained in a given set. To begin with, let us introduce a concept, antisymmetry.

Definition. (Antisymmetry)
Given a relation $R$ on a set $A$ , antisymmetry is defined as

$\left( \forall x,y\in A\right) \left( (x,y),(y,x)\in R\Rightarrow x=y \right)$

Definition. (Partial Ordering)
A set $A$ is a partially ordered set or poset, if the relation $R$ on the set $A$ is reflexive, antisymmetric, and transitive.

The only difference with an equivalence relation is antisymmetry vs symmetry. Note that antisymmetry is not $(x,y)\in R \Rightarrow (y,x)\notin R$ .

Extending the idea of partial ordering, now we introduce the supremum, or least upper bound, and the infimum, or greatest lower bound.

Definition
For a partial order $R$ for a set $A$ and $B \subseteq A$ ,
* $a$ is an upper bound for $B$ if $(b,a)\in R$ for all $b\in B$ .
* $a$ is a lower bound for $B$ if $(a,b)\in R$ for all $b\in B$ .
* $a$ is a supremum for $B$ , denoted $sup(B)$ , if

1. $a$ is an upper bound for $B$ , and
2. $(a,x)\in R$ for every upper bound $x$ for $B$

* $a$ is an infimum for $B$ , denoted $inf(B)$ , if

1. $a$ is a lower bound for $B$ , and
2. $(x,a)\in R$ for every lower bound $x$ for $B$

Let us illustrate with an example.

Example. Show that if $sup(B)$ exists, it is unique, where $R$ is a partial order for a set $A$ and $B \subseteq A$ .

Proof.
Let both $x$ and $y$ be least upper bounds for $B$ .
Then, both $x$ and $y$ are upper bounds.
Then, by definition of supremum, $(x,y),(y,x)\in R$ .
Then, $x=y$ by antisymmetry.

13 Relations

Relations

Equivalence Relations

Ordering Relations

License

Share This Book