23 Rings
The definitions of ring and field were provided in the former section, Proofs, Bridge, and Analysis, where we explored the completeness of real numbers ![]() . As such, in this section we briefly revisit the definition of each and go over a few examples, and then move onto integral domain, a commutative ring without 0.
. As such, in this section we briefly revisit the definition of each and go over a few examples, and then move onto integral domain, a commutative ring without 0.
A ring is a notion expanded on a group. A ring ![]() is a set with 2 binary operations, specifically, addition (
is a set with 2 binary operations, specifically, addition (![]() ) and multiplication (
) and multiplication (![]() ), whereas a group
), whereas a group ![]() is a set with a single binary operation defined on the set
is a set with a single binary operation defined on the set ![]() . Note that the binary operation, denoted by
. Note that the binary operation, denoted by ![]() , need not be one of four arithmetic operations (
, need not be one of four arithmetic operations (![]() ).
).
As a ring is defined upon two operations, namely addition (![]() ) and multiplication (
) and multiplication (![]() ), establishing a ring homomorphism naturally involves meeting the two conditions as follows:
), establishing a ring homomorphism naturally involves meeting the two conditions as follows:
Given a mapping of rings ![]() , for all
, for all ![]() ,
,
Fields
We succinctly defined a field as a commutative division ring. As such, let us formally define a commutative ring and a division ring, and move onto a field.
Definition. (Commutative and Division Ring)
A commutative ring is a ring that the multiplication is commutative.
A division ring is a ring that every non-zero element is a unit, where a unit refers to an element that has a multiplicative inverse.
Therefore, a field, a commutative division ring, is a ring that multiplication is commutative and every non-zero element has a multiplicative inverse. Indeed, a field is a specific type of a ring. We can define another special case of a ring, a nonzero commutative ring, which is called an integral domain and will be discussed in the following section.
Integral Domains
Since the restriction non-zero is included in the definition of an integral domain, let us discuss the notion of the divisors of 0 (or 0 divisors), and then an integral domain.
Definition. (Divisors of 0)
For ![]() of a ring
of a ring ![]() ,
, ![]() and
and ![]() are the divisors of 0 if
are the divisors of 0 if
![]()
where ![]() and
and ![]() .
.
Definition. (Integral Domain)
An integral domain is a commutative ring, where
- the unity, the identity element of multiplication,
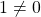 is included; and
is included; and - there are no divisors of 0
In other words, in an integral domain,
![]()
since there are no 0 divisors.
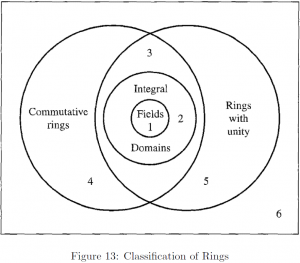
Following diagram shows the position of an integral domain as a specific type of a ring. Therefore, a field is indeed an integral domain, and a commutative ring with unity (i.e. a commutative division ring).
It naturally follows the cancellation laws hold in an integral domain from the fact an integral domain has no 0-divisors. In fact, they are equivalent propositions, as the following theorem [9] shows:
Theorem. (Cancellation Laws Hold is equivalent to having no 0-divisors)
A ring where cancellation laws hold is a ring with no divisors of 0.
Proof.
The proof is divided into two parts.
1. Cancellation laws hold implies no 0-divisors
Suppose a ring ![]() , where cancellation laws hold, and let
, where cancellation laws hold, and let ![]()
Then,
- When
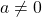
Then,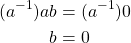
- When
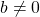
Then,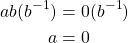
Therefore,
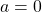 or
or 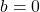 , and thus there can be no 0-divisors.
, and thus there can be no 0-divisors.
2. no 0-divisors implies Cancellation laws hold
Suppose a ring ![]() with no divisors.
with no divisors.
Let ![]() , where
, where ![]() .
.
Then,
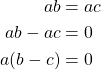
Then, ![]() and thus
and thus ![]() , since
, since ![]() has no 0-divisors and
has no 0-divisors and ![]() .
.
Likewise, the assumption ![]() for
for ![]() leads to
leads to ![]() and thus
and thus ![]() , since, again,
, since, again, ![]() has no 0-divisors and
has no 0-divisors and ![]() .
.
Therefore, a ring where cancellation laws hold is a ring with no 0-divisors.
Therefore, we can say an integral domain is a ring that cancellation laws hold. We conclude this section introducing the characteristic of the ring, and move onto the rings of polynomials.
Definition. (Characteristic of the Ring)
The characteristic of the ring ![]() is defined as the least
is defined as the least ![]() such that
such that
![]()
for all ![]() , if such
, if such ![]() exist. Otherwise, the characteristic of the ring is defined as 0.
exist. Otherwise, the characteristic of the ring is defined as 0.
