16 Section Summary

In this section, we have discussed relations, functions, and cardinality, stemming from the set theory and its operations. The readers should note this summary is brief, only the essence of essentials are contained, leaving out a substantial chunk behind. To name a few of left-out parts, they are

• In set theory, extended set operations, indexed families of sets, power sets, and principles of counting;
• In relations, exploration on partitions, Hasse diagram, linear or total order relation, and well-ordering theorem;
• In functions, many different kind of functions, such as characteristic functions, and image and pre-image of sets; and
• In cardinality, the comparison and ordering of cardinal numbers, specifically, the proof of 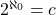, the axiom of choice, and the Hilbert’s paradox of the Grand Hotel.

Solid understanding of this summary would be a good stepping stone to explore the vast arena of mathematics.