21 Section Summary

In this section, we have discussed axioms and topology of real numbers, particularly fields and ordering, and revisited sequences, limits, and continuity. Again, it is always the author’s regret to wish this summary were longer. Thus we conclude this chapter introducing more items to be explored as follows:

• In axioms of 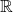, a lot of theorems and their proofs had to be omitted for brevity, and the notion of fields and rings were only briefly introduced; in modern algebra, these will be revisited and stem from the group theory. Also, equivalent expressions of Archimedian property were omitted.
• In topology of 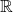, another important theorem, the Bolzano-Weierstrauss Theorem was omitted. More importantly, in fact, the completeness of 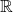, the Bounded Monotone Sequence Theorem, the Heine-Borel Theorem, and the Bolzano-Weierstrauss Theorem are all equivalent, one implying another and forming a loop.
• In sequences, there are many more theorems of sequences and subsequences to be explored.
• In limits and continuity, the neighborhood on a number line can evolve into a disk when the notion is applied on a complex plane, and continuity can also be discussed in metric spaces.

Again, it is the reader’s role to “fill in the gaps.”