6 Sequences and Series
A sequence is a list of numbers in a definite order:
![]()
Usually sequences are written inside curly brackets:
![]() or
or ![]()
The limit of a sequence ![]() ,
, ![]() , may or may not exist. We say a sequence converges or is convergent when the limit exists, and diverges or is divergent when the limit does not exist. For example, the sequence
, may or may not exist. We say a sequence converges or is convergent when the limit exists, and diverges or is divergent when the limit does not exist. For example, the sequence ![]() diverges, since
diverges, since ![]() , and the sequence
, and the sequence ![]() diverges, since
diverges, since ![]() .
.
Some important traits of sequences are defined as follows:
Definition. (Monotonic Sequence)
If ![]() for all
for all ![]() , then the sequence
, then the sequence ![]() is increasing, and likewise, if
is increasing, and likewise, if ![]() for all
for all ![]() , then the sequence
, then the sequence ![]() is decreasing. Either increasing or decreasing, the sequence is called monotonic.
is decreasing. Either increasing or decreasing, the sequence is called monotonic.
Definition. (Bounded Sequence)
If ![]() for all
for all ![]() , then the sequence
, then the sequence ![]() is bounded above, and likewise, if
is bounded above, and likewise, if ![]() for all
for all ![]() , then the sequence
, then the sequence ![]() is bounded below. Either bounded above or below,
is bounded below. Either bounded above or below, ![]() is a bounded sequence.
is a bounded sequence.
Consequently, we arrive at a theorem.
Theorem. (Monotonic Sequence Theorem).
If a sequence is bounded and monotonic, then the sequence is convergent.
Proof.
Suppose a sequence is divergent. Then, the sequence has no bound or is alternating – as in a repetition of a certain loop or as in the decimals of an irrational number. Alternating sequence is not monotonic. Therefore, a divergent sequence has no bound or not monotonic. Then, taking the contrapositive, if a sequence is bounded and monotonic, then the sequence is convergent.
It is interesting to see each partial sum up to the ![]() -th term of a sequence
-th term of a sequence ![]() generates another sequence
generates another sequence ![]() . We call this
. We call this ![]() , a series, where
, a series, where ![]() . For convergent series, we write
. For convergent series, we write
![]()
There are in fact numerous kind of series. Let us begin our exploration with a geometric series.
Geometric series takes the form
![]()
where ![]() .
.
Let us find a condition for convergence of a geometric series.
![]()
Then, ![]() . Note that
. Note that ![]() for
for ![]() . Therefore, for
. Therefore, for ![]() ,
,
![]()
Let us utilize the geometric series formula with an example.
Example. Evaluate ![]() .
.
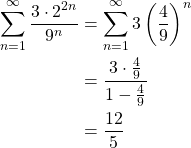
Another type of interesting series is a telescoping series. Its name originates from the cancellation involved in the solution path and only a handful of terms remain as a result, as a telescope is collapsed. Again, let us illustrate with an example.
Example. Find the sum ![]() if convergent.
if convergent.
![Rendered by QuickLaTeX.com \begin{align*} &\sum_{n=1}^{\infty} \frac{1}{n(n+1)}\\ = &\sum_{n=1}^{\infty} \left( \frac{1}{n} - \frac{1}{n+1}\right)\\ = &\lim_{n \to \infty} \left[ \left( 1-\frac{1}{2}\right) + \left( \frac{1}{2} - \frac{1}{3}\right) + \left( \frac{1}{3} - \frac{1}{4} \right) + \cdots + \left( \frac{1}{n}-\frac{1}{n+1}\right)\right]\\ = &\lim_{n \to \infty} \left( 1-\frac{1}{n+1}\right)\\ = &1 \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7edeb7ca1c88b007681ecc8f92bbfa28_l3.png)
Seemingly a similar one, called a harmonic series, in fact diverges to ![]() . Let us examine.
. Let us examine.
Example. Find the sum ![]() if convergent.
if convergent.
Note that ![]() is in fact the right-hand Riemann sum of
is in fact the right-hand Riemann sum of ![]() to estimate
to estimate ![]() .
.
Therefore,
![Rendered by QuickLaTeX.com \begin{align*} \sum_{n=1}^{\infty} \frac{1}{n} &= 1+\frac{1}{2}+\frac{1}{3}+\cdots + \frac{1}{n}+\cdots\\ &> \int_{1}^{\infty} \frac{1}{x}\,dx\\ &= \lim_{t \to \infty} \int_{1}^{t} \frac{1}{x}\,dx\\ &= \lim_{t \to \infty} \left[ \ln|x|\right]_1^t\\ &= \lim_{t \to \infty} \ln|t|\\ &= \infty \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9a0d73f88112c4d28eee7286d631aaec_l3.png)
Therefore, ![]() diverges to
diverges to ![]() .
.
The technique we just used in determining the convergence of the harmonic series is called an integral test (for the convergence of a series), when a given series can be interpreted as a Riemann sum of a function ![]() and thus compared with
and thus compared with ![]() .
.
Let us further examine the series in the form of ![]() by conducting an integral test. What would be the condition for this series to converge?
by conducting an integral test. What would be the condition for this series to converge?
Let ![]() . Then,
. Then,
![Rendered by QuickLaTeX.com \begin{align*} \sum_{n=1}^{\infty}\frac{1}{n^p} &= 1+\frac{1}{2^p}+\frac{1}{3^p}+\cdots + \frac{1}{n^p}+\cdots\\ &> \int_{1}^{\infty} \frac{1}{x^p}\,dx\\ &= \lim_{t \to \infty} \int_{1}^{t} x^{-p}\,dx\\ &= \lim_{t \to \infty} \left[ \frac{x^{-p+1}}{-p+1}\right]_{1}^{t}\\ &= \lim_{t \to \infty} \frac{1}{1-p}\left[ \frac{1}{t^{p-1}}-1\right] \end{align*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c6f2449866a6da7dbcf824bdcc0cf689_l3.png)
1. ![]()
Then, ![]()
2. ![]()
Then, ![]()
Therefore, the condition for the convergence of the ![]() -series
-series ![]() can be summarized as:
can be summarized as:
The ![]() -series is convergent if and only if
-series is convergent if and only if ![]() ; otherwise divergent.
; otherwise divergent.
Now we come to think what is a condition for any series to converge. Let us suppose a series converges, i.e. there exists ![]() such that
such that ![]() . Also, by definition, we can write the
. Also, by definition, we can write the ![]() -th term of the sequence
-th term of the sequence ![]() as
as ![]() . Then,
. Then,
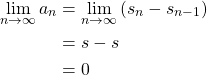
Above can be succinctly summarized as follows:
Theorem. If the series ![]() is convergent, then
is convergent, then ![]() .
.
In other words, taking the contrapositive of the theorem,
Corollary. (Test for Divergence)
If ![]() does not exist or
does not exist or ![]() , then the series
, then the series ![]() is divergent.
is divergent.
To examine the convergence of a given series, so far we have conducted integral tests. The comparison test is essentially the same in that we compare a given series with a known series that converges or diverges. For example,
Example. Determine the convergence of ![]() .
.
In fact, we know ![]() converges and
converges and ![]() . Therefore,
. Therefore,
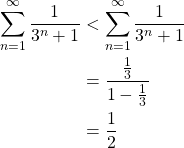
Therefore, the series ![]() converges (to a value smaller than
converges (to a value smaller than ![]() ).
).
The technique we used in fact is called a comparison test. To formally write,
Theorem. (Comparison Test)
For converging series ![]() and
and ![]() with positive terms,
with positive terms,
- If
 diverges, then
diverges, then 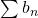 diverges.
diverges. - If
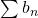 converges, then
converges, then 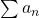 converges.
converges.
Now, suppose we are interested in determining the convergence of ![]() . In this case, the comparison test
. In this case, the comparison test ![]() does not help. Instead, we can utilize another technique called the limit comparison test.
does not help. Instead, we can utilize another technique called the limit comparison test.
Theorem. (Limit Comparison Test)
For converging series ![]() and
and ![]() with positive terms, if
with positive terms, if
![]()
then the convergence of both series is the same, i.e. either both diverge or both converge.
Therefore, we conclude ![]() is convergent, since
is convergent, since
![]()
Let us consider a different kind of series, an alternating series, having ![]() within its term. A series
within its term. A series ![]() is an e example of alternating series. In fact, there is a test for convergence for certain types of alternating series.
is an e example of alternating series. In fact, there is a test for convergence for certain types of alternating series.
Theorem. (Alternating Series Test)
For decreasing sequence ![]() with
with ![]() , its alternating series
, its alternating series
![]()
is convergent.
Let us illustrate with an example.
Example. Determine the convergence of ![]() .
.
Let ![]() . Then,
. Then,
1. ![]() is a decreasing sequence, since
is a decreasing sequence, since ![]() for all
for all ![]()
2. ![]()
Therefore, by alternating series test, the series ![]() is convergent.
is convergent.
Now, let us introduce the concept of absolute convergence.
Definition. (Absolute Convergence)
A series ![]() is absolutely convergent if
is absolutely convergent if ![]() is convergent.
is convergent.
The notion of absolute convergence was needed for the ratio test. The ratio test is highly useful a test in determining the convergence of a series. The ratio is defined as follows:
Theorem. (Ratio Test)
Given
![]()
- If
 , then the series
, then the series 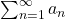 is absolutely convergent.
is absolutely convergent. - If
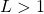 , then the series
, then the series 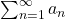 is divergent.
is divergent. - If
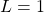 , then the test is inconclusive.
, then the test is inconclusive.
Let us illustrate with an example.
Example. Determine the convergence of ![]() .
.
Let us conduct the ratio test. Then,
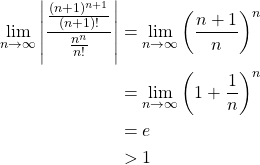
Therefore, by the ratio test, the series ![]() is divergent.
is divergent.
We conclude this section introducing a similar, but another useful test, the root test.
Theorem. (Root Test)
Given
![]()
- If
 , then the series
, then the series 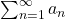 is absolutely convergent.
is absolutely convergent. - If
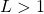 , then the series
, then the series 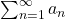 is divergent.
is divergent. - If
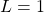 , then the test is inconclusive.
, then the test is inconclusive.
