12 Set Theory
The set theory is a branch of mathematical logic studying sets. Let us begin with the formal definition of a set.
![]()
denotes the collection of elements, represented by ![]() , defined by
, defined by ![]() , a one-variable open sentence describing the properties of the set. Following is an example of expressing the same set.
, a one-variable open sentence describing the properties of the set. Following is an example of expressing the same set.
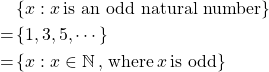
How is an empty set, denoted ![]() , without any elements? In fact, an empty set is the empty set, i.e. the set without any element is unique. Formally the empty set or null set is defined as
, without any elements? In fact, an empty set is the empty set, i.e. the set without any element is unique. Formally the empty set or null set is defined as
Definition. (The Empty Set or Null set)
![]()
So, we can see formally the empty set is defined as a contradiction, that the empty set is the collection of elements such that ![]() is not
is not ![]() itself, which can never be true.
itself, which can never be true.
Next, we move on to the definition of a subset. We say one set is a subset of another set when every element of the former set is also the element of the latter set. Therefore, technically every set is the subset of the set itself, but in this case, we call this a trivial subset; otherwise, non-trivial or proper subsets. Formal definition of a subset is as follows:
Definition. (Subset)
![]()
where ![]() means “for all” or “every”.
means “for all” or “every”.
Therefore, to prove one set is a subset of another set, we take the following approach:
Direct Proof of ![]() .
.
Let ![]() be an arbitrary object.
be an arbitrary object.
Suppose ![]() .
.
![]()
Then, ![]() .
.
Therefore, ![]() .
.
How about the equality of two sets? Intuitively we would think any given two sets are the same, i.e. equal, whenever the elements included in each set are identical. However, individually examining every element of each set would not be so efficient, or infeasible, when the number of elements is large, or even impossible when the number of elements is infinitely many, either countable or not. Therefore, we need a strategy, and typically the proof of the equality of sets takes the form:
Proof of the Equality of Sets ![]() and
and ![]() .
.
1. Prove ![]() .
.
2. Prove ![]() .
.
3. Therefore, ![]() .
.
Let us illustrate with an example.
Example. Prove ![]() , where
, where ![]() and
and ![]() .\,
.\,
1. Prove ![]() .
.
Let ![]() .
.
Then, ![]() by definition of
by definition of ![]() .
.
Then,
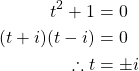
Therefore, if ![]() , then
, then ![]() .
.
Therefore, ![]() .
.
2. Prove ![]() .
.
Use brute force.
![]()
Also,
![]()
Therefore, ![]() for all
for all ![]() , i.e.
, i.e. ![]() .
.
3. Therefore, by 1. and 2., ![]() .
.
Set Operations
Now we turn to set operations, operations between multiple sets. First, binary, involving only 2 sets, operations are introduced.
Definition.
Let ![]() and
and ![]() sets.
sets.
The union of ![]() and
and ![]() is the set
is the set ![]() .
.
The intersection of ![]() and
and ![]() is the set
is the set ![]() .
.
The difference of ![]() and
and ![]() is the set
is the set ![]() .
.
Consider a case where there is no common element between the two sets ![]() and
and ![]() , i.e.
, i.e. ![]() . Then, we call the sets
. Then, we call the sets ![]() and
and ![]() are disjoint.
are disjoint.
So far we have discussed sets defined without giving any reference to a source, i.e. we simply referred an element to be arbitrary, where the universe it comes from was not defined. In fact, defining the boundary for the universe yields another useful concept complement. To define formally,
Definition.
Let ![]() be the universe, where
be the universe, where ![]() .
.
The complement of ![]() is the set
is the set
![]()
Exploring with the definitions introduced so far, we can reach a few theorems as follows:
Theorem.
Let ![]() be the universe, where
be the universe, where ![]() . Then,
. Then,
1. Inclusion Property
![]()
2. Commutativity
![]()
3. Associativity
![]()
4. Distributivity
![]()
5. DeMorgan’s Laws
![]()
The commutative, associative, and distributive laws also uphold in set operations as in the case of algebraic binary operations – all 3 laws hold in multiplication; and associativity and commutativity hold in addition. We conclude this section with the proof of DeMorgan’s Laws for set operations.
Proof of DeMorgan’s Laws.
1. ![]()
(a) ![]()
Let ![]() .
.
Then, ![]() and
and ![]() .
.
Then, ![]() and
and ![]() .
.
Then, ![]() and
and ![]() .
.
Then, ![]() and
and ![]() .
.
Then, ![]() and
and ![]() .
.
Therefore, ![]() .
.
(b) ![]()
Follow in the reverse order of the proof above.
Therefore, by (a) and (b), ![]() .
.
2. ![]()
(a) ![]()
Let ![]() .
.
Then, ![]() and
and ![]() .
.
Then, ![]() and
and ![]() .
.
Then, ![]() and
and ![]() .
.
Then, ![]() or
or ![]() .
.
Then, ![]() or
or ![]() .
.
Therefore, ![]() .
.
(b) ![]()
Follow in the reverse order of the proof above.
Therefore, by (a) and (b), ![]() .
.
