Topology of Real Numbers

Donovan D Chang

18 Topology of Real Numbers

We are only short of one axiom, the completeness axiom to fully describe the set $\mathbb{R}$ of real numbers as a complete ordered field. Let us recall the hierarchy of number sets

$\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}\subset \mathbb{C}$

In fact, both $\mathbb{Q}$ and $\mathbb{R}$ , the sets of rational numbers and real numbers, are ordered fields, yet the only difference lies in completeness. In other words, rational numbers cannot complete a horizontal number line. We can easily demonstrate this by placing the bottom left corner of a unit square on the origin and draw an arc whose radius is the diagonal of the unit square. By the Pythagorean Theorem we know the length of the diagonal, i.e. the radius, is

$\sqrt{2}=\sqrt{1^2+1^2}$

which cannot be expressed as a fraction, and thus an irrational number.

Therefore, intuitively we can understand the denumerability and incompleteness of rational numbers on the number line (to be precise, rational numbers cannot form a line but a series of dots), and by taking irrational numbers into account the number line becomes complete and continuous.

Now, let us complete the rational number line and turn it into a real number line.

The Completeness Axiom

Roughly or intuitively, the completeness axiom can be stated as [14]:

For a given ordered field,

“Between any two distinct elements there is a third element”
“There are never any empty spaces between elements”
There does not exist “the next rational number” or “the next real number” on the number line

After revisiting the definitions of upper and lower bounds in partial ordering, we formally define the completeness. The only difference here is the relation $R$ is replaced with “ $\leq$ ”

Definition. (Bounded)

Let $A\subseteq F$ , where $F$ is an ordered field. Then,

$A$ is bounded above if $A$ has an upper bound.
$A$ is bounded below if $A$ has a lower bound.
If bounded above and below, then $A$ is bounded.

Definition. (Completeness of an Ordered Field [14])
An ordered field $F$ is complete iff every nonempty subset of $F$ with an upper bound has a supremum, i.e. least upper bound, in $F$ .

Let us illustrate with an example.

Example. Let $A$ , $B$ , and $A+B$ be subsets of $\mathbb{R}$ , where

$A=\left\lbrace a_1,a_2,\cdots,a_n\right\rbrace$ ,
$B=\left\lbrace b_1,b_2,\cdots,b_n\right\rbrace$ , and
$A+B=\left\lbrace a_i+b_i:1\leq i \leq n\right\rbrace$ for $n\in \mathbb{N}$ .

Prove $A+B$ is bounded above.

$\mathbb{R}$ is closed in addition, since $\mathbb{R}$ is a complete ordered field.
Therefore, all elements of $A+B$ are real numbers.
Then, by the completeness axiom, $sup(A+B)$ exists and is in $\mathbb{R}$ .
Therefore, $A+B$ is bounded above.

One important consequence of the completeness axiom is the Archimedean Property.

Theorem. (Archimedean Property)
The set $\mathbb{N}$ of natural numbers is unbounded above in $\mathbb{R}$ .

Proof.
We shall prove by contradiction, and thus let us suppose the negation, that the set $\mathbb{N}$ of natural numbers is bounded above in $\mathbb{R}$ .
Then, by the completeness axiom, $\mathbb{N}$ has a supremum $m$ , i.e. $sup(\mathbb{N})=m$ .
Then, $m-1$ is not an upper bound of $\mathbb{N}$ .
Then, there exists $n\in \mathbb{N}$ such that $n>m-1$ .
Then, $n+1\in \mathbb{N}$ , where $n+1>m$ .
This is contradiction to $sup(\mathbb{N})=m$ .

Therefore, we conclude the set $\mathbb{N}$ of natural numbers is unbounded above in $\mathbb{R}$ .

Heine-Borel Theorem

We shall conclude this section with the Heine-Borel Theorem, a major result yielded from the completeness of real numbers. To do so, we need familiarize ourselves with the concepts of neighborhood, cover and subcover, and closed, open, and compact sets. Let us begin with a neighborhood.

Definition. ( $\delta$ -Neighborhood of $x$ )
For $x,\delta\in\mathbb{R}$ , where $\delta >0$ , the set $\delta$ -neighborhood of $x$ is defined as

$\mathcal{N}(x,\delta) = \left\lbrace z\in \mathbb{R}:|z-x|<\delta\right\rbrace$

That is, the set $\delta$ -neighborhood of $x$ can be thought as the collection of points whose distance is less than $\delta$ from $x$ , i.e. the points in the disk with radius $\delta$ but exclusive of the boundary. This neighborhood concept was introduced to formally define an interior point of an interval in $\mathbb{R}$ . That is,

Definition. (Interior Point)
For a set $A\subseteq\mathbb{R}$ , a point $x$ is an interior point of $A$
iff there exists a neighborhood of $x$ in $A$ , i.e. $\mathcal{N}(x,\delta)\subseteq A$ .

Utilizing the notion of a neighborhood, for example, for an interval $(0,2)$ , any point between 0 and 2, but except the boundary 0 and 2 themselves, is an interior point, since owing to the completeness or continuity of real numbers, we can define a neighborhood, no matter how small the radius may be, around the point. Now, we define an open and a closed set.

Definition. (Open and Closed Sets)
The set $A\subseteq\mathbb{R}$ is

open iff every point of $A$ is an interior point of $A$ .
closed iff 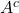$A^c$ is open, i.e. every point of 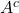$A^c$ is an interior point of $A^c$ .

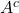Naturally, we reach the following theorem.

Theorem.
Every open interval of real numbers is an open set.

Armed with the notion of open and closed sets, we introduce cover and subcover of a set.

Definition. (Cover and Subcover)
For a set $A\subseteq\mathbb{R}$ , a collection $\mathcal{C}$ of open subsets of $\mathbb{R}$ is a cover for $A$ , that is,

$A\subseteq \bigcup_{C\in \mathcal{C}}C$

If $\mathcal{B}$ is also a cover for $A$ , where $\mathcal{B}\subseteq \mathcal{C}$ , then $\mathcal{B}$ is a subcover of $\mathcal{C}$ .

Let us illustrate with an example.

Let $A=\left\lbrace 1,3,5,7,9 \right\rbrace$ and $\mathcal{C}=\lbrace (0,2),(2,4),(4,6),(6,8),(8,10) \rbrace$ . Then, $\mathcal{C}$ is a cover for $A$ , since

$A\subseteq \bigcup_{C\in \mathcal{C}}C=(0,10)\setminus \left\lbrace 2,4,6,8 \right\rbrace$

What is, and why do we need cover? To illustrate this, we can use the sun-ray-shade analogy [14]. The cover $\mathcal{C}$ of $A$ can be viewed as a cover providing shade for the set $A$ underneath from sun’s rays. Note that $\mathcal{C}$ is not itself a single long cover, but as a union of its elements serves as a cover.

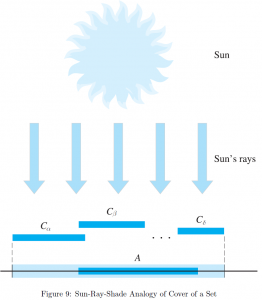
In fact, we only gave an answer to the question, what a cover is with an analogy. Now we think about why we need the concept of a cover – it was for the notion of a compact set, and the famous Heine-Borel Theorem provides another equivalent form of an expression as follows:

Definition. (Compact Set)
The set $A\subseteq\mathbb{R}$ is compact
iff for every cover $\mathcal{C}$ for $A$ , there is a finite subcover $\mathcal{B}\subseteq \mathcal{C}$ .

Theorem. (Heine-Borel Theorem)
The set $A\subseteq\mathbb{R}$ is compact
iff $A$ is closed and bounded.

We only briefly summarize the Heine-Borel Theorem as a compact set is equivalent to a set being closed and bounded. This topic will be revisited in a later section dealing uniform continuity.

18 Topology of Real Numbers

The Completeness Axiom

Heine-Borel Theorem

License

Share This Book