Linear Algebra

Donovan D Chang

Linear Algebra

In the former section, linear algebra was briefly introduced as the systems of linear equations, where a system is consistent when there exists a set of solutions satisfying all the equations; and otherwise inconsistent.

Let us have a look at how the term linear algebra is defined in the dictionaries.

“The part of algebra that deals with the theory of linear equations and linear transformation” [4]
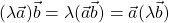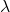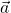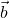“A finite-dimensional vector space, with multiplication defined and distributive over addition, in which $(\lambda \vec{a})\vec{b}=\lambda (\vec{a}\vec{b})=\vec{a}(\lambda \vec{b})$ for any scalar $\lambda$ of the associated field and any vectors $\vec{a}$ and $\vec{b}$ ; also, the branch of algebra which deals with the properties of these entities, especially of vector spaces over the real or complex numbers” [5]

The first definition focuses on “what”, the contents of linear algebra, and the second, defining linear algebra as a vector space, though a bit narrow, provides a good overview.

In fact, linear algebra was not initially invented, but rather evolved into current understanding of vector space as we studied a set of linear equations involving multiple variables. To demonstrate, let us first define a linear equation.

Definition. (System of Linear Equations)
A linear equation with variables $x_i$ and coefficients $a_i$ for $i=1,2,\cdots,n$ is an equation that can be written in the following form:

$\sum_{i=1}^{n}a_ix_i=a_1x_1+a_2x_2+\cdots +a_nx_n = b$

A system of linear equations or simply a linear system is a collection of linear equations, and such system with $j$ variables in $i$ equations would have a form:

$\begin{align*} a_{11}x_1+a_{12}x_2+ &\cdots +a_{1j}x_j = b_1\\ a_{21}x_1+a_{22}x_2+ &\cdots +a_{2j}x_j = b_2\\ &\vdots\\ a_{i1}x_1+a_{i2}x_2+&\cdots +a_{ij}x_j = b_i \end{align*}$

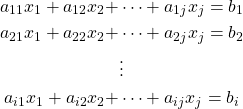
However, as the equations get bulky, it becomes inconvenient to write the same variables over and over again. Therefore, we invented a clever way to express the same idea using matrices and vectors. Note that a matrix with only one column is called a (column) vector.

Expressing the system of linear equations introduced above using matrices, it becomes a matrix equation as follows:

$\left( \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1j} \\ a_{21} & a_{22} & \cdots & a_{2j} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{ij} \end{array} \right) \left( \begin{array}{c} x_1\\ x_2\\ \vdots\\ x_j \end{array} \right) = \left( \begin{array}{c} b_1\\ b_2\\ \vdots\\ b_i \end{array} \right)$

or simply, omitting the variables, the system can be expressed in an augmented matrix form,

$\left( \begin{array}{cccc|c} a_{11} & a_{12} & \cdots & a_{1j} & b_1 \\ a_{21} & a_{22} & \cdots & a_{2j} & b_2 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{ij} & b_i \end{array} \right)$

If we denote the coefficient matrix, and the column of $x_i$ ‘s and $b_i$ ‘s as $A$ , $\vec{x}$ and $\vec{b}$ , respectively, then it can be as succinct as

$A\vec{x}=\vec{b}$

The system can also be expressed as a vector equation as follows:

$\begin{align*} \sum x_j \vec{a_j} &= \sum \left[ x_j \left(\begin{array}{c} a_{1j}\\ a_{2j}\\ \vdots\\ a_{ij} \end{array}\right) \right]\\ &= x_1 \begin{pmatrix} a_{11}\\ a_{21}\\ \vdots\\ a_{i1} \end{pmatrix} + x_2 \begin{pmatrix} a_{12}\\ a_{22}\\ \vdots\\ a_{i2} \end{pmatrix} + \cdots + x_j \begin{pmatrix} a_{1j}\\ a_{2j}\\ \vdots\\ a_{ij} \end{pmatrix} &= \begin{pmatrix} b_1\\ b_2\\ \vdots\\ b_i \end{pmatrix} = \vec{b} \end{align*}$

Linear System as Linear Transformation

Note that the vector $\vec{x}\in \mathbb{R}^j$ is transformed into $\vec{b}\in \mathbb{R}^i$ by multiplication of the coefficient matrix $A$ . Therefore, another way of viewing a linear system is as a linear transformation, mapping, or function $T$ such that $T:\mathbb{R}^j \rightarrow \mathbb{R}^i$ by the rule $A$ .

One might as well wonder whether one notation has superiority over the rest. In fact, it is not the case, but rather there are instances where one notation is more intuitive and thus preferred. Now, armed with various notations for systems of linear equations, let us begin our exploration.

Definition. (Consistent and Inconsistent Linear System)
A linear system can be consistent with

a unique set of solution(s); or
infinitely many sets of solution(s)

or inconsistent with no solutions.

Let us illustrate with an example.

Example. Find the solution(s) of the given linear system.

For $x,y\in \mathbb{R}$ ,

$\begin{align*} x+2y &=5\\ x-2y &=-3 \end{align*}$

Adding the 2 equations we have

$\begin{align*} 2x &= 5-3 = 2\\ x &= 1\\ \therefore y &= \frac{5-x}{2}\\ &= \frac{5-1}{2}\\ &= 2 \end{align*}$

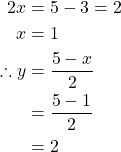
Example. Find the solution(s) of the given linear system.

\item For $x,y\in \mathbb{R}$ ,

$\begin{align*} x+y &=2\\ -x-y &=-2 \end{align*}$

Let us equate $y$ with algebraic manipulations. Then,

$2-x=y=-x+2=2-x$

In fact, one equation is a scalar multiple}, by -1, of the other.
Therefore, the information the 2 equations gives us is identical.
Therefore, the system is consistent for all $x,y\in \mathbb{R}$ such that $x+y=2$ .
Therefore, we conclude the solution set is

$\lbrace (x,2-x):x\in \mathbb{R}\rbrace$

In a parametric vector form},

$\vec{x}= x\begin{pmatrix} 1\\ -1 \end{pmatrix} + \begin{pmatrix} 0\\ 2 \end{pmatrix} \text{ for } x\in \mathbb{R}$

since

$\vec{x} = \begin{pmatrix} x\\ y \end{pmatrix} = \begin{pmatrix} x\\ 2-x \end{pmatrix} = \begin{pmatrix} x\\ -x \end{pmatrix} + \begin{pmatrix} 0\\ 2 \end{pmatrix}\\ = x\begin{pmatrix} 1\\ -1 \end{pmatrix} + \begin{pmatrix} 0\\ 2 \end{pmatrix}$

Example. Find the solution(s) of the given linear system.

For $x,y\in \mathbb{R}$ ,

$\begin{align*} x+y &=2\\ -x-y &=2 \end{align*}$

Again, let us equate $y$ with algebraic manipulations. Then,

$2-x=y=-2-x$

Then,

$0\cdot x=4$

There does not exist $x\in \mathbb{R}$ satisfying $0\cdot x=4$ .
Therefore, we conclude the system is inconsistent}.

Linear Algebra

License

Share This Book