Mathematical Models
What is a mathematical model, and why do we need it? Before thinking about a mathematical model, let us narrow our focus down to just a model. What is a model? The Oxford [6] definition states
“a simplified description, especially a mathematical one,
of a system or process, to assist calculations and predictions”
From the author’s viewpoint, this definition in fact appears a bit too narrow, in that (i) it only mentions the role of a model to assistance in calculations and predictions, while it is one of the major functions of a model; and thus (ii) the mention on the particular usage in mathematics naturally following from the computation focus.
Maybe one way of defining a model is as a simplification of reality, a real-world phenomenon. The key is how to construct a frame with key relevant factors, i.e. variables, to reflect reality – what happened in the past and what is happening in the present tense, usually called the validation of a theory, as well as make accurate predictions about the future. Naturally mathematics is used as a tool in the construction and validation of a model, but math itself is not the core of the model.
Another thing to note about a model is, while the aim is to explain a phenomenon as well as make predictions, the model itself need not correctly reflect or resemble the reality. This might sound like a contradiction on the surface, but in fact is not.
A Nobel prize-winning danish physicist Niels Bohr demonstrated quantized energy levels in hydrogen atom with a model called Bohr’s atomic hydrogen model, which can be succinctly summarized with the following formula:
![Rendered by QuickLaTeX.com \[ \frac{1}{\lambda}=R_H \left( \frac{1}{n_f^2}-\frac{1}{n_i^2}\right)\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f30ac4f80b7be8920e45e20929960673_l3.png)
where ![]() denotes the wavelength of the electromagnetic radiation emitted;
denotes the wavelength of the electromagnetic radiation emitted; ![]() is the Rydberg constant for hydrogen; and
is the Rydberg constant for hydrogen; and ![]() and
and ![]() are initial and final energy levels of an electron, respectively.
are initial and final energy levels of an electron, respectively.
The above equation works well with remarkable accuracy, in fact almost perfect, at least with respect to the hydrogen atom, however does not to other atoms. In the Bohr model, Bohr specified specific energy levels, i.e. radii, that the electrons orbit, however later this model was superseded by the atomic orbital model based on probability theory. That being said, Bohr’s atomic hydrogen model does not resemble reality, and nor a correct reflection of reality, and yet the beauty of his model is it works, at least for hydrogen atom. This is a striking example demonstrating the utility of a model lies in its capacity to explain and make predictions of a phenomenon, but not in its actual resemblance of reality.
In fact, there are numerous kinds of models, and diverse ways of classifying them. As the space restriction would not allow us to go over them all individually, instead, we only introduce select models of key importance. The first to be introduced is a linear model in the form of
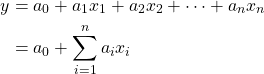
where ![]() ‘s are independent variables for
‘s are independent variables for ![]() .
.
Those that do not take the linear form are considered nonlinear. Nonlinear models may include trigonometric terms (e.g. ![]() ), power terms
), power terms ![]() , and product terms
, and product terms ![]() , where
, where ![]() for
for ![]() . Note that in some cases nonlinear models can be linearized. That is, for example, where a supposed relationship is
. Note that in some cases nonlinear models can be linearized. That is, for example, where a supposed relationship is ![]() , by examining the relationship of
, by examining the relationship of ![]() vs
vs ![]() , instead of ordinary
, instead of ordinary ![]() vs
vs ![]() , we can build a linear model.
, we can build a linear model.
Another important division is by the inclusion of time-dependent term(s). Models that do not account for the element of time is called a static model, and they model systems in equilibrium. On the contrary, some models include, or are defined by, time-dependent terms, such as ![]() or
or ![]() , where the inclusion of former or the latter is called modelling with difference or differential equation, respectively.
, where the inclusion of former or the latter is called modelling with difference or differential equation, respectively.
Also, the distinction between a deterministic vs probabilistic model warrants our attention. The change or evolution in our view on atoms, specifically on the orbits of electrons, from orbiting certain specified energy levels, that can be defined with a deterministic wave equation in the Bohr’s atomic hydrogen model, to orbitals, regions with increased likelihood of spotting electrons, expressed as probabilistic equations, is one such example. However, this does not mean a probabilistic model is superior to a deterministic model, but should be understood as, at least for the modelling of electron behaviors, a probabilistic model was found to be more suitable.
We note again it is not possible to introduce and go over all the models listed above in this summary, and if so, the author fears this summary would end up being a very brief description of a great miscellanea, containing little to no actual content of each. Therefore, instead, we shall pick and choose, and focus on a handful amount of models, maybe two or three, and discuss those to some extent. Our first topic is a linear model.
