Modern Algebra
What is modern algebra? Another name for modern algebra is abstract algebra. Before we think about modern or abstract algebra, let us first think about algebra. Following is the definition from the Oxford Dictionary [3]:
“The part of mathematics in which letters and other general symbols
are used to represent numbers and quantities in formulae and equations”
The above definition provided by Oxford most closely reflects the traits of elementary algebra and linear algebra. In elementary algebra, we learn
- four basic arithmetic operations: addition, subtraction, multiplication, and division (
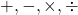 );
); - the concepts of \emph{known} and \emph{unknown} variables, where the latter, the unknown, is most often denoted by
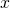 ;
; - how to simplify mathematical expressions,
e.g.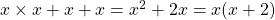 ; and
; and - how to set up equations and inequalities, and some basic techniques how to solve them.
Linear algebra primarily deals with systems of linear equations, whether the solutions are real or complex numbers, referring to the system consistent, when there exists a solution, and inconsistent otherwise. As we deal with multiple variables, it becomes cumbersome to write the same variables over and over again, and thus we introduce the notion of vector. Also, almost always is the case a linear system is comprised of multiple equations, and these can be conveniently handled in a matrix form, either as a stack of vertical (column) vectors, or horizontal (row) vectors.
Finally we turn our focus to abstract algebra. Indeed, as implied from the name, it is algebra of abstract nature. To be specific, instead of the results of binary operations themselves and finding a solution to given equations or inequalities, our focus is on the process and a pattern, or collectively an algebraic structure.
Following is an illustrative example. Try to spot the similarity in the process.
- 0 in addition
For any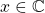 ,
,
![Rendered by QuickLaTeX.com \[ x+0=0+x=x\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fa76219b979ee6ec7f1f2af1ec8636a7_l3.png)
- 1 in multiplication
For any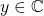 ,
,
![Rendered by QuickLaTeX.com \[ y\cdot 1=1\cdot y=y\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ad3fa7fc8f9028d3cce921d251a84830_l3.png)
- Identity element
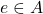 of a binary operation
of a binary operation  defined on
defined on  .
.
For any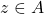 ,
,
![Rendered by QuickLaTeX.com \[ z*e=e*z=z\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-968a6914f826dff1c2b4f5af568d6578_l3.png)
Here is another example.
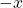 of
of 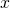 in addition
in addition
For any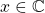 ,
,
![Rendered by QuickLaTeX.com \[ x+(-x)=(-x)+x=0\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-67ae43a51f8f449f4bca8c4c259a39ed_l3.png)
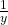 of
of 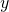 in multiplication
in multiplication
For any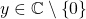 ,
,
![Rendered by QuickLaTeX.com \[ y\cdot \frac{1}{y}=\frac{1}{y}\cdot y=1\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-44644290839b6cf70cb5237f568449ec_l3.png)
- Inverse
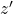 of
of  , given a binary operation
, given a binary operation  defined on
defined on  .
.
For any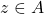 , there exists
, there exists 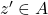 such that
such that
![Rendered by QuickLaTeX.com \[ z*z'=z'*z=e\]](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f6aaa7668b633b5838d5706f13fbecdf_l3.png)
Did you spot a pattern, or similarity? Let us begin our exploration to formally define what we have just observed.
