Real Analysis

Donovan D Chang

Real Analysis

This section is titled “Real Analysis”. Indeed, we shall study the analysis of real numbers. But let us think about why the analysis of real numbers is so important warranting a separate section. To do so, let us recall our discussion so far and the expansion and hierarchy of numbers or number sets.

Function is one of key concepts in mathematics, and for deeper understanding we have covered logic and some proof techniques, followed by sets and set theory, and then relations and functions with counting elements. The vast majority of functions we deal with are real-valued, and as such, it warrants solid understanding in number systems, specifically how our notion of numbers have evolved, from natural numbers, to whole numbers with the introduction of $0$ , to integers with negative numbers, to rational numbers expressed in fractions, to real numbers which includes irrational numbers whose decimal numbers are infinite without a pattern, then finally to complex numbers with the invention of a notion $\sqrt{-1}=i$ .

Let us think about numbers. Following is a list of a few random numbers:

$-2, 0,\frac{3}{2}, \sqrt{3}, \pi, 1+i\sqrt{2}, \sin i$

As our theory and understanding in mathematics advanced, we have defined and developed the following commonly-used number sets:

Natural numbers, $\mathbb{N}=\left\lbrace 1,2,3,\cdots \right\rbrace$
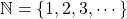
Integers, $\mathbb{Z} = \left\lbrace 0,\pm 1,\pm 2,\pm 3,\cdots \right\rbrace$
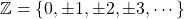
Rational Numbers, $\mathbb{Q}=\left\lbrace \frac{p}{q}:p,q\in \mathbb{Z} \text{ and } q\neq 0 \right\rbrace$
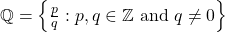
Real Numbers, denoted $\mathbb{R}$
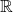
Complex Numbers, $\mathbb{C}=\left\lbrace x+iy:x,y\in \mathbb{R} \text{ where }i^2=-1 \right\rbrace$

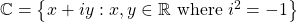
with hierarchy

$\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}\subset \mathbb{C}$

Note that the definition for real numbers were not provided above. In this section, we shall discuss what makes a real number real, i.e. conditions or axioms to “fill the gaps” of the countably many rational numbers, with cardinality $\aleph_0$ to become real numbers whose cardinality is continuum $c$ .

In fact, there are two approaches to describe real numbers. One is a constructive approach, that is, we begin from the number sets of a lower hierarchy, for example, natural numbers $\mathbb{N}$ and then add conditions to evolve the number set into the ones upper in the ladder. The other is an axiomatic approach, which we shall take in this section, to first provide axioms, propositions accepted as is but not tested, which incorporates all the traits of number sets of lower hierarchy.

At the end of this section, the reader will be surprised to see how the notions and concepts of mathematics are connected and intertwined, as we revisit sequences, limits, and continuity.

Real Analysis

License

Share This Book