5.9   Exponential Functions

 

India was the second most populous country in the world, with a population of about 1.25 billion people, in 2013. According to Worldometer (http://www.worldometers.info/world- population/), on February 24, 2014, the population was growing at a rate of about 1.2% each year. If this rate continues, the population of India will exceed China’s population by the year 2031. When populations grow rapidly, we often say the growth is “exponential.” To a mathematician, however, the term exponential growth has a very specific meaning. In this section, we will take a look at exponential functions, which model this kind of rapid growth.

 

Learning Objectives: In this section, you will learn about the properties and characteristics of exponential functions. Upon completion you will be able to:

• Apply the laws of exponents to simplify exponential expressions.
• Identify an exponential function.
• Classify the graphs of exponential functions as growth or decay models.
• Memorize the graph of the parent exponential growth or decay model.
• Determine the domain of an exponential function, using interval notation.
• Solve equations involving exponential functions with like bases.
• Solve equations involving exponential functions which can be rewritten with like bases.
• Use exponential functions to model real-world situations, and use them to solve application problems.

Reviewing Laws of Exponents

Recall from the Power and Radical Functions section, we reviewed some basic properties of variables raised to numerical exponents. These properties also hold true when numerical values are raised to variable exponents, as follows.

Note: Parentheses are stated when needed. Do not assume parentheses where there are none.

 

abx =×axbx a · bx ×= (ab)x

 

When a real number is raised to a variable exponent, the real number is called the base.

Example 1: Using the Laws of Exponents, rewrite 85x−7 as an equivalent expression in base 2.

Solution: For 85x−7, 8 is the base. An equivalent form of 8, in base 2, is 23. Using this fact and the rule (ax)y = axy, we have

85x−7 = 23 5x−7

= (2)3·(5x−7)

= 215x−21

Example 2: Using the Laws of Exponents, completely simplify 27 · 73x+1 ./72x

Solution: We begin by eliminating the fraction, using the rule ax/ay = ax−y .

27 73x+1

72x           = 27 · 7

 

(3x+1)−(2x)

= 27 · 7x+1

Since 27 does not have a factor of 7, no further simplification is necessary. We cannot combine unlike base factors to make a single base. So,

72x           = 27 · 7

x+1

When combining like base factors, we combine the exponents, but keep the common base. For example,

73x+1 · 7−2x = 7x+1 but 73x+1 · 7−2x ×= 49x+1

 

Describing Exponential Functions

 

In the definition of a general exponential function the base is positive and not equal to 1.

• If the base were a negative number, say b = −2, then the function f(x) = a . (−2)x has trouble. For instance, when x = 12, a . (−2)12 = a .√−2, which is not a real number. In general, if x is any rational number (in simplest terms) with an even denominator, then (−2)x is not defined. Therefore, we must restrict our attention to bases where b ≥ 0.

• If the base were equal to 0, the function f(x) = a . 0x is undefined for x ≤ 0, because we cannot divide by 0 and 0x is unclear as x approaches 0 or ∞.

• If the base were equal to 1, the function would be of the form f(x) = a . 1x. So, f(x) can be simplified to f(x) = a for any finite real number x, which has the behavior of a constant function. However, the behavior of f(x) = a . 1x is unclear as x approaches Å}∞. The authors will leave this special case to higher level mathematics. Thus, the authors will require the base to be positive and not equal to 1 in discussions concerning exponential functions in this text.

Note: Power functions are of the form f (x) = a xp, and exponential functions are of the form g(x) = a bx. While the two functions look similar, they are not the same. Power functions have a variable base and a constant exponent, whereas exponential functions have a constant base and a variable exponent.

Example 3: Determine whether or not each of the following are exponential functions. If the function is exponential, state whether it represents exponential growth or decay.

(a) f(x) = 43x

(b) g(x) = x3

(c) h(x) =13x

(d) j(x) = (−5)x

Solution: (a) f (x) = 43x can also be written as f (x) = (43)x = 64x, using the Laws of Expo- nents. In both forms, the base is a real number constant which is greater than 0 and not equal to 1, and the exponent contains the variable. Thus, f (x) IS an exponential function. Because the base, in either form, is greater than 1,f(x) is an exponential growth function.

(b)   g(x) = x3 has a variable base and a real number constant exponent. Thus, g(x) is NOT an exponential function. Instead, g(x) is a power function; in particular, g(x) is a cubic polynomial.

(c) h(x) =13x has a base of b = 13 and a variable exponent. With b > 0 and b  = 1, h(x) IS an exponential function. Because 0 < b < 1, h(x) is an exponential decay function.

(d) j(x) = (−5)x has a base of b = −5 and a variable exponent. Due to the fact that b < 0, j(x) is NOT an exponential function.

 

 

Properties of Exponential Functions

For us to gain a clear understanding of exponential growth, let us contrast exponential growth with linear growth. We will construct two functions. The first function, f (x) = 2x, is exponential. The second function, g(x) = 2x, is linear. We will start with an input of 0, and increase each input by 1. Table 5.15 shows the consecutive outputs of f (x) are doubled, while the consecutive outputs of g(x) only increase by 2.

 

x	f (x) = 2x	g(x) = 2x
0	1	0
1	2	2
2	4	4
3	8	6
4	16	8
5	32	10
6	64	12

Table 5.15: A chart comparing exponential and linear growth.

From Table 5.15 we can infer that for these two functions, exponential growth dwarfs linear growth.

• Exponential growth refers to the original value from the range increasing by the same percentage over equal increments found in the domain.
• Linear growth refers to the original value from the range increasing by the same amount over equal increments found in the domain.

We can also see from Table 5.15, the difference between “the same percentage” and “the same amount” is quite significant. For exponential growth, over equal increments, the constant multiplicative rate of change resulted in doubling the output whenever the input increased by one. For linear growth, the constant additive rate of change over equal increments resulted in adding two to the output whenever the input was increased by one.

In general, if the constant multiplicative rate of change or constant additive rate of change is known, then the corresponding output for a 1 unit input change can be found from the previous output, without having an actual function rule specified. Let’s now reconsider the function f (x) = 2x from Table 5.15 over a different interval, [ 3, 3]. Table 5.16 shows the corresponding outputs for each input.

insert chart

 

Table 5.16: A chart of values for f (x) = 2x over the interval [−3, 3].

To construct a more accurate graph, we need to consider what would happen as x → ±∞.

For example, 2−100 ≈ 7.8886 × 10−31 is positive, but very close to 0. On the other hand, 2100 ≈ 1.2677 × 1030, which is also positive, but very large.

Let us examine the graph of f (x) by plotting and connecting the ordered pairs from Table 5.16 and drawing the end behavior according to our further calculations, as in Figure 5.6.2.

 

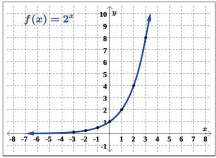
Some observations from Figure 5.6.2 are

• The domain is (−∞,∞).
• The range is (0,∞).
• The end behavior shows as x→−∞, f(x) → 0; there is a horizontal asymptote (HA) at y = 0.
• The end behavior shows as x→∞, f(x)→∞.
• The graph of f(x) will never touch the x-axis, because base 2 raised to any real number exponent never has the result of zero. Thus, there are no x-intercepts.
• The y-intercept is (0, 1).

Note: We could have rewritten f(x) = 2x as f(x) =1/2−x, using the Laws of Exponents. Now, let’s consider the function g(x) =1/2x= 0.5x. We will again create a table (Table 5.17) to determine the corresponding outputs over the interval [−3, 3].

insert chart

 

Table 5.17: A chart of values for g(x) = ( 1 )x over the interval [−3, 3].

Again, to construct a more accurate graph, we will consider what would happen as x → ±∞. For example,  1.2677 10  is positive, but very large. On the other hand, ( 1 )100 ≈ 7.8886 × 10−31 is also positive, but very close to 0.

We will graph g(x) in Figure 5.6.3, using the ordered pairs from Table 5.17 and drawing the end behavior according to our further calculations.

 

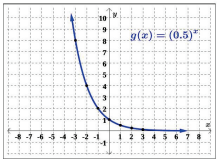
Some observations from Figure 5.6.3 are

• The domain is (−∞,∞).
• The range is (0,∞).
• The end behavior shows as x→−∞, g(x)→∞.
• The end behavior shows as x→∞, g(x) → 0; there is a horizontal asymptote (HA) at y = 0.
• The graph of g(x) will never touch the x-axis, because base 1/2 raised to any real number exponent never has the result of zero. Thus, there are no x-intercepts.
• The y-intercept is (0, 1).

Note: We could have rewritten g(x) = ( 1 )x as g(x) = 2−x, using the Laws of Exponents. We can generalize our observations.

Properties of General Exponential Functions

For any real number x, nonzero real number a, and a real number b where b > 0 but b = 1, the general exponential function

f(x) = a . bx

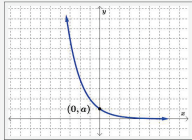
has the following properties. If a > 0 and 0 < b < 1, then

• The domain is (−∞,∞).
• The range is (0,∞).
• There are no x-intercepts.
• The y-intercept is (0, a).
• The end behavior is
• As x→−∞, f(x)→∞
• As x→∞, f(x) → 0 (H.A. y = 0)

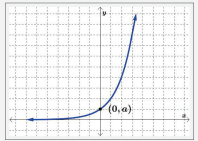
If a > 0 and b > 1, then

• The domain is (−∞,∞).
• The range is (0,∞).
• The end behavior is
  • – As x→−∞, f(x) → 0 (H.A. y=0)
  • – As x→∞, f(x)→∞
• There are no x-intercepts.
• The y-intercept is (0, a).

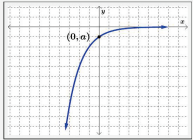
If a < 0 and 0 < b < 1, then

• The domain is (−∞,∞).
• The range is (−∞, 0).
• There are no x-intercepts.
• The y-intercept is (0, a).
• The end behavior is:
  • – As x→−∞, f(x)→−∞
  • – As x→∞, f(x) → 0 (H.A. y=0)

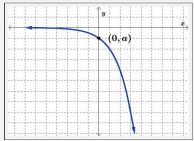
If a < 0 and b > 1, then

• The domain is (−∞,∞).
• The range is (−∞, 0).
• There are no x-intercepts.
• The y-intercept is (0, a).
• The end behavior is:
  • – As x→−∞, f(x) → 0
  • – As x→∞, f(x)→−∞ (H.A. y=0)

The properties of any general exponential function vary depending on the values of both a and b. We will now add the parent functions for exponential growth and decay to our list of parent functions. Notice these parent functions, shown in Table 5.18, have a = 1.

Name                        Function                           Graph                 Table        Domain

 

 

Table 5.18: Parent Exponential Growth and Decay Functions

Example 4: Given h(x) = 3 · ( 1 )x, state each of the following.

(a)   Domain                                              (d)   x-intercept(s)

(b)   Range

(c)   End behavior                                     (e)   y-intercept(s)

 

Solution: We begin by recognizing b = 1(0 < b < 1), and a = 3 > 0. From this information, we note h(x) is an exponential decay function, and thus, we have the following results.

(a)   The domain of h(x) is (−∞, ∞).

(b)   The range of h(x) is (0, ∞).

(c)   The end behavior of h(x) is

•  As x → −∞, h(x) → ∞.

•  As x → ∞, h(x) → 0.

(d)   h(x) has no x-intercepts.

(e)   h(x) has a y-intercept at (0, h(0)) = (0, a) = (0, 3).

 

Of all the bases for exponential functions, two occur the most often in real-world scenarios. The first, base 10, is often called the common base. The second base is the irrational num- ber e  2.718, called the natural base. So, f (x) = 10x and g(x) = ex are both exponential growth functions and h(x) = 10−x and k(x) = e−x are both exponential decay functions.

 

Note: A more formal discussion of the origins of the irrational number e is left to calculus.

 

 

 

Computing Domain

We have seen for b > 0 and b = 1,f(x) = bx has a domain of all real numbers. Now suppose h(x) = bg(x), where b > 0 and b = 1, and g(x) is any previously discussed function. Then, h(x) is defined wherever g(x) is defined.

 

Example 5: State the domain of each function, using interval notation.

(a) f(x)=3−x+2

(b) h(x) = 10 2 x−1

(c) j(x) = 1 e√2x+5

Solution:   (a) f (x) = 3−x+2 is defined when g(x) = −x + 2 is defined. Considering g(x) is a polynomial and defined for all real numbers, the domain of f (x) is (−∞, ∞).

(b) h(x) = 10 2

x−1 is defined when g(x) = 2

x−1 is defined. As g(x) is a rational function,

we must find all values of x where x − 1  = 0.

x − 1  = 0

x  = 1

Thus, the domain of h(x) is (−∞, 1) ∪ (1, ∞).

e√2x+5 can be written as j(x) = e−√2x+5, using the Laws of Exponents. So

(c) j(x) = 1

j(x) is defined when g(x) = −√2x + 5 is defined. Because g(x) is an even root function, it is defined where 2x + 5 is defined and greater than or equal to 0. As 2x + 5 is a polynomial expression defined for all real numbers, we must satisfy

2x + 5 ≥ 0

2x ≥ −5

x ≥ −52

Thus, the domain of j(x) is  −52 , ∞ .

 

Solving Equations Involving Exponential Expressions

In this chapter, thus far, we have solved equations involving polynomials. Now, we will explore equations involving exponential expressions.

 

Note: This is often called the One-to-One Property of Exponents. We will discuss what one-to-one means in a later section of this chapter.

 

In other words, Theorem 5.6 says that when an equation has an exponential expression with the same base on each side of the equals sign, the exponents must be equal. This also applies when the exponents are algebraic expressions. Therefore, we can solve many of these types of equations by using the Laws of Exponents to rewrite each side as an exponential expression with the same base. Then, we can set the exponents equal to one another, and solve for the

3

unknown. Consider how to solve the equation 34x−7 = 32x for x.

 

We begin by rewriting the right-hand side so that both sides have a single expression with the common base, 3. Then, we apply the Common Base Property of Exponents by setting the exponents equal to each other, and solve for x.

 

 

34x−7 =

 

34x−7 =

32x 3

32x

31

34x−7 = 32x−1

4x − 7 = 2x − 1

2x = 6

x = 3

Example 6: Solve 25x = √2 for x.

Solution: First, we rewrite √2 in its equivalent exponent form.

25x = √2

2

25x = 2( 1 )

 

Now that both sides of the equation have a single exponential expression with a common base of 2, we can apply the Common Base Property, and solve for x.

1

5x =

2

1

x =

10

Example 7: Solve 9x−1 = 92x−4 for x.

Solution: Both sides of the equation already have a single exponential expression with the same base, so we can apply the Common Base Property, and solve for x.

9x−1 = 92x−4

x − 1 = 2x − 4

−x = −3

x = 3

 

e5x

Example 8: Solve  1  = ex2−6 for x.

Solution: We will again start by rewriting the left-hand side to have a single exponential expres- sion with a common base on both sides of the equals sign. To do so, we will use the Laws of Exponents.

1

 

 

e5x

= ex2−6

e−5x = ex2−6

 

Now that there is a single exponential expression with a common base on both sides, we set the exponents equal, and solve for x.

2

−5x = x − 6

0 = x2 + 5x − 6

0 = (x + 6)(x − 1)

x + 6 = 0     or     x − 1 = 0

x = −6     or     x = 1

Sometimes the common base for a exponential equation is not explicit. In these cases, we simply rewrite the terms in the equation as exponential expressions with a common base raised to an appropriate power, and then solve using Laws of Exponents and the Common Base Property.

Consider the equation 256 = 4x−5.

While there does not appear to be a common base, we can rewrite both 256 and 4 as powers of 2. Then, we can apply the Laws of Exponents, along with the Common Base Property, to solve for x.

 

 

 

 

 

 

 

 

 

 

Example 9: Solve 8x+2 = 16x+1 for x.

256 = 4x−5

(   )

28 = 22 x−5

28 = 22x−10

8 = 2x − 10

18 = 2x

9 = x x = 9

Solution: While both sides of the equation have an exponential expression with different bases, we can rewrite each base as a power of 2. Then, we can proceed as before.

(   )        (   )

8x+2 = 16x+1

23 x+2 =  24 x+1

23x+6 = 24x+4

3x + 6 = 4x +4

2 = x x = 2

 

Not all equations involving exponential expressions have a solution. Recall that the range of an exponential function is always positive. So, while solving an equation involving expo- nentials, we may obtain an expression which is undefined.

 

To demonstrate, consider 3x = −2. We have an exponential function (3x) set equal to a non-positive number, so there is no value of x where 3x = −2.

Similarly, e−x = 0 has no solution, as 0 is not a positive number.

When an equation has multiple terms on one or both sides of the equal sign, it is important to move all terms to the same side of the equals sign (as with quadratic equations) before solving for x.

 

Example 10: Solve x2ex − 3xex = 10ex for x.

Solution: First, we move all terms to the same side of the equals sign, leaving 0 on the other side.

 

 

Factoring gives us

x2ex − 3xex = 10ex

x2ex − 3xex − 10ex = 0

 

 

(                )

ex x2 − 3x − 10 = 0

ex(x − 5)(x + 2) = 0

ex = 0      or     x − 5 = 0      or     x + 2 = 0

ex ×= 0      or     x = 5 or     x = −2

Thus, x = −2 or x = 5.

 

 

Applying Exponential Functions to Real-World ApplicationsAt the beginning of this section, we learned that the population of India was about 1.25 billion in the year 2013, with an annual growth rate of about 1.2%. Assuming this situation is represented by the growth function P (t) = 1.25(1.012)t, where t is the number of years since 2013 and P is the population (in billions), what will the population be in 2031?

 

To estimate the population in 2031, we evaluate the model for t = 18, because 2031 is 18 years after 2013.

P (18) = 1.25(1.012)18 ≈ 1.549

So, there will be about 1.549 billion people in India in the year 2031.

 

Savings instruments in which earnings are continually reinvested, such as mutual funds and retirement accounts, use compound interest. The term compounding refers to interest earned not only on the original value, but on the accumulated value of the account.

 

The annual percentage rate (APR) of an account, also called the nominal rate, is the yearly interest rate earned by an investment account.

We can calculate the compound interest using the compound interest formula, which is an exponential function of the values time (t), principal (P ), APR (r), and number of compounding periods in a year (m).

m

A(t) = P  1+  r  mt

For example, observe Table 5.19, which shows the result of investing $1000 at 10% for one year. Notice how the value of the account increases, as the compounding frequency increases.

 

Frequency	m	Value after 1 year
Annually	1	$1100.00
Semiannually	2	$1102.50
Quarterly	4	$1103.81
Monthly	12	$1104.71
Weekly	52	$1105.06
Daily	365	$1105.16

Table 5.19: Compounding results for a principal of $1000.

 

Example 11: If we invest $3000 in an investment account paying 3% interest per year, compounded quarterly, how much will the account be worth in 10 years?

Solution: Because we are starting with $3000,P = 3000.  Our annual interest rate is 3% so r = 0.03. As we are compounding quarterly, we are compounding 4 times per year, so m = 4. We are asked the value of the account in 10 years, so we are looking for A(10), the value when t = 10. Using this information in the formula, we have

m

)

A(t) = P  1+  r  mt

 

A(10) = 3000

0.03  4·10

1+

4

≈ $4045.05

 

The account will be worth about $4045.05 in 10 years.

 

When dealing with dollar amounts, round your final answer to the nearest cent, when not told otherwise.

Example 12: A 529 Plan is a college-savings plan that allows relatives to invest money to pay for a child’s future college tuition; the account grows tax-free. Lily wants to set up a 529 account for her new granddaughter and wants the account to grow to $40, 000 over 18 years. She believes the account will earn 6% annual interest, compounded semiannually. To the nearest dollar, how much will Lily need to invest in the account now?

Solution: The nominal interest rate is 6%, so r = 0.06. Interest is compounded semiannually, or twice a year, thus, m = 2. The account grows over 18 years, giving us t = 18. We want to calculate the initial investment, P , needed so that the value of the account will be worth $40, 000 in 18 years, A(18) = 40000. Using the formula gives us

m

)

A(t) = P  1+  r  mt

 

A(18) = 40000 = P

0.06  2·18

1+

2

40000 = P (1.03)36

40000

(1.03)36 = P

P ≈ 13801

 

Lily will need to invest approximately $13, 801 now, in order to have $40, 000 in 18 years.

In the applications thus far, we have worked with rational bases for exponential functions. For most real-world phenomena, however, the irrational number e is used as the base for exponential functions.  Exponential models that use e as the base are called continuous

growth or continuous decay models. We see these models in finance, computer science, and most of the sciences, such as physics, toxicology, and fluid dynamics.

 

 

When using a function involving the natural base, e, always use the ex option found on your calculator.

Example 13: Radon-222 decays at as continuous rate of 17.3% per day. How much will 100mg of Radon-222 decay to in 3 days?

−

Solution: Seeing as the substance is decaying, the rate 17.3% is negative. So, r =  0.173. As the initial amount of Radon-222 was 100mg,a = 100. We use the continuous decay function to compute the value after t = 3 days, as follows:

A(t) = aert

A(3) = 100e−0.173·3

≈ 59.5115

So, approximately 59.5115mg of Radon-222 will remain.

Example 14: A person invested $15,000 in an account earning 2% interest per year, compounded continuously. How much will be in the account at the end of seven years?

Solution: Considering the account is growing continuously in value, this is a continuous com- pounding problem with a growth rate of r = 0.02. The initial investment was $15, 000, so P = 15000. We use the continuous compounding function to calculate the value after t = 7 years, as follows:

A(t) = Pert

A(7) = 15000e0.02·7

≈ 17254.11

The account is worth about $17, 254.11 after seven years.

 

 

TryItAnswers1.      (a) True

(b)   False

(c)   True

2.      (a) Not exponential

(b)   Exponential growth

(c)   Exponential decay

3.      (a) (−∞, ∞)

(b)   (0, ∞)

(c)   As x → −∞,f(x) → 0

As x → ∞,f (x) →∞

(d)   None

(e)

2

(0, 1)

4.      (a) (7, ∞)

(b)   (−∞, ∞)

(c)   (−∞, ∞)

5.   x = −2

6.   x = −1

7.   x = 0 or x = 8

8.   1.548 billion people

9.     (a) $3, 644, 675.88

(b)   $3, 659, 823.44

10.   $14, 278.55

Exercises 

Basic Skills Practice 

For Exercises 1 – 4, rewrite each exponential expression as a single equivalent expression in the stated base.

 

1.   163x, base 4

2.   125x−7, base 5

3.   163x, base 2

4.   81x+4, base 3

For Exercises 5 – 8, determine whether or not each of the following are exponential functions.

 

5.   f (x) = 711x

6.   h(x) = (−5)x

7.   g(x) = x2/3

8.

8

j(x) = ( 3 )−x

For Exercises 9 – 12, state the following properties of the exponential function.

(a)  Domain                                         (d) x – intercept(s)

(b)  Range                                             (e) y – intercept(s)

(c)  End behavior

9.   f (x) = 22x

10.   h(x) = (0.4)x

11.   g(x) = (  1  )x

12.

3

15

j(x) = ( 8 )x

For Exercises 13 – 16, state the domain of the function, using interval notation.

13.   f (x) = 3x−4

14.   h(x) = e3x−11

15.   g(x) = ( 1 )x

16.

2

7x−9

j(x)=  8

For Exercises 17 – 19, algebraically solve each equation for x.

 

17.   15x = 153

18.   9x2 = 9

19.   (3x−1)4 = 3

For Exercises 20 – 23, algebraically solve each equation for x.

 

20.   4x = 8

21.   27x+534x = 9

22.   252x = 1259x−4

23.   4x−123x = 84

For Exercises 24 – 25, the model for continuous (exponential) growth/decay is given by

y = cekt

where c is the initial amount, k is the relative growth rate (as a decimal), t is time (in years), and y is the amount after t years.

24.   A new piece of equipment worth $100, 000 depreciates continuously at a relative rate of 7% per year. What will it be worth in 8 years, to the nearest dollar?

25.   If $2500 is invested in an account that earns interest at a rate of 3.87% per year, compounded continuously, how much will be in the account (to the nearest cent) after 10 years?

 

 

 

Intermediate Skills Practice 

For Exercises 26 – 29, rewrite each exponential expression as a single equivalent expression in the stated base.

26.   7 · 492x−3, base 7

27.   121 · 111+4x, base 11

28.

64

(  1  )4−6x, base 2

29.

36

(  1  ) · 68x+3, base 6

For Exercises 30 – 33, state whether the exponential function represents exponential growth or decay.

30.   f (x) = 0.5x

31.   h(x) = 2−10x

32.   g(x) = ( 7 )x

33.

6

4

j(x) = ( 1 )−3x

For Exercises 34 – 37, state the following properties of the exponential function.

(a)  Domain                                         (d) x – intercept(s)

(b)  Range                                              e. y – intercept(s)

(c)  End behavior

34.   f (x) = 4ex

35.   h(x) = 6 · (0.12)x

36.   g(x) = − (  1  ) · 35x

37.

9

15

j(x) = −11 · ( 2 )x

ex+2

For Exercises 38 – 41, state the domain of the function, using interval notation.

 

38.

x

f (x) = ex−6

40. g(x) = √7−x

) = 5

39. h(x

√4 x+3

41.      j(x) = 2 √9 12+x

x2−1

For Exercises 42 – 45, algebraically solve each equation for x.

 

42.      6x2 = 6x+12

43.      ex2 · e−4x = e12

44.        1  = 28x−11

 

45.

26x

e9x

1  = e5x+7

For Exercises 46 – 53, algebraically solve each equation for x.

 

46.      85−7x · 86x = 1

47.      0.04 = 53x · 5−2x2

50. 85−7x · 86x = 1

51. 0.04 = 53x · 5−2x2

48.

2

x2+23

29x            = 8

x2+23

52.

2

29x            = 8

6−4x

6−4x

49. 36x2 ·   1  − 1 = 0                                          53. 36x2 ·   1  − 1 = 0

54.      How much should you invest now (to the nearest cent) in an account that earns interest at a rate of 7.2% per year, compounded continuously, in order to have $100, 000 in 20 years?

55.      If you invest $1500 in an account that earns interest at a rate of 4.1% per year, com- pounded quarterly, how much will be in the account (to the nearest cent) after 6 years?

56.      How much money should you invest now (to the nearest cent) in an account that earns interest at a rate of 5.75% per year, compounded monthly, in order to have $85, 000 in 14 years?

 

 

 

Mastery Practice 

53.      Using the Laws of Exponents determine if the following statements are true or false.

 

(a)     5·4x+7

 

16·4x−2

= 81920

(b)   3 · 256x+1 = 756x+1

54.      Use the Laws of Exponents, to write 9·27−4x

3·81x+9

 

as a single equivalent expression in base 3.

55.

2

Determine if g(x) = 3 · ( 1 )x is an exponential growth or decay function.

56.      Determine if h(x) = c−x, where c is a real number and c > 8.5, is an exponential growth or decay function. 57.

57.      For f (x) = 5−x, state the following properties of the exponential function.

(a)  Domain                                      (d) x – intercept(s)

(b)  Range                                           e. y – intercept(s)

(c)  End behavior

e√x+9

58.      State the domain of f (x) = √5 x

, using interval notation.

+1

x+2

4 √8x−1

59.      State the domain of g(x) = √8 3 − x , using interval notation.

60.      Algebraically solve x2e3x + 2xe3x − 8e3x = 0 for x.

61.      Algebraically solve x · 10−x = x2 · 10−x for x.

62.      Algebraically solve x · 32x − x · 273x+1 = 0 for x.

63.      Determine how much money (to the nearest cent) needs to be invested in an account earning 6.7% interest per year, so that the account contains $90, 000 after 15 years, if the interest is compounded

 

(a)   Semiannually.

(b)   Weekly.

(c)   Daily.

(d)   Continuously.