Logic

Maggie Schildt

10 Logic

As mentioned at the end of the last chapter, proofs are vital to any work we do in mathematics. Without proofs, any solution we find remains unsupported. Throughout our time in school and our careers we are asked to show our work. We must provide some sort of thought process and note the steps we took to come to various conclusions. When we compile all this information neatly into a report we have created a proof. There is no theorem, corollary or calculation that does not require a proof in order to support the claim. Proofs usually begin with a claim or statement by which we must either prove or disprove by using various rules and techniques that will be provided in this chapter. There are many different kinds of proofs and we will cover them in the subsequent subsections as well. Firstly, we must discuss logic which will provide the fundamental keys to visualizing and constructing proofs.

Before we can consider proof techniques, we have to discuss logic. Logic provides a set rules by which we follow in order to structure a proof. How a spinal cord is to a complete human body, logic is to a complete proof. Logic consists of a series of statements or propositions denoted by $P$ and $Q$ generally that must be determined to be either true or false. No logic statement can be inconclusive. Logic allows us to truly study a problem and break it down in order to better choose the best strategies to create a proof. We will look at logic through the following truth tables.

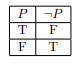
Logical Negation

Logical negation is when we are given a proposition $P$ that has been negated as denoted by $\neg P$ . This is considered the opposite of the proposition $P$ . How this effects the proposition’s truth value is seen in the truth table below.

Example:

Given the claim “I am happy”, denoted by $P$ , the negation is the proposition “I am not happy”, denoted by $\neg P$ . If “I am happy” is true then the claim “I am not happy” is a lie, or false, and if $P$ is false, then $\neg P$ is true.

We provide examples like this because it reminds us of the real-world application that logic can play in areas like programming. Where we need to put in rules for true of false statements and then denote what will follow based on the logic outcome.

Logical Conjunction

A conjunction involves two statements denoted $P$ and $Q$ that are connected by “and” which is represented by $\wedge$ . In the following truth table, we see that this requires both propositions to be true in order for the conjunction to be true.

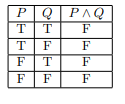
Here we see that the only time the outcome of a logic conjunction is true is when both $P$ and $Q$ are true. This easily makes sense because $P \wedge Q$ cannot be both true and false, thus we say the conjunction is false because either $P$ or $Q$ is not true. As well if $P$ and $Q$ are both false then of course the logical conjunction is false.

Logical Disjunction

Logical disjunction is similar to logical conjunction, involving $P$ and $Q$ but instead of being joined by the operator “and” $P$ and $Q$ are joined by “or”, represented by $\vee$ . In the following logic table for disjunction we will see that disjunction is quite inclusive in the sense that if one proposition or both are true then the disjunction is also true.

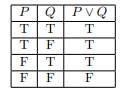
Here we are given the flexibility of only one claim needing to be true in order for the disjunction to be true. Thus, we can observe that the only time we may have a false disjunction is when both claims are false then neither claim is true so the disjunction is false.

Logical Implication

A logical implication requires $P$ to now represent a hypothesis and $Q$ to know represent a conclusion. We denote an implication by “ $\Rightarrow$ ” which means “if, then” or “only if”. Logical Implication in terms of truth values suggests that if the conclusion is true then the implication is true; as well if the hypothesis and the conclusion have the same truth value then the implication is true. See the logic table below.

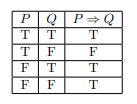
In this table we can see that if $P$ and $Q$ have the same truth value then the implication is true. This would make sense when we consider our that if our initial claim $P$ implies the same truth value as another claim $Q$ then the implication should be true. Now if we consider the times when our initial claim $P$ ends up being false but our other claim $Q$ is true regardless then the implication is still true. To counter this though, if $P$ is true but $Q$ is false then the implication is false, because $Q$ was false.

Logical Biconditional

With a biconditional statement, we have two statements that depend solely on each other. Their interaction is a conditional statement $P$ and its converse $Q$ . We denote a biconditional by ⇔ which represents an “if and only if” statement. The truth table is given below.

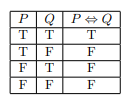
We might consider a biconditional statement to be a two way street. If $P$ then $Q$ and if $Q$ then $P$ , the one key take away is that the truth value for the biconditional statement is exclusive the truth value of both $P$ and $Q$ . This is different than what we saw in the implication statement because we could have a true implication but $P$ could be false. Here, we need both $P$ and $Q$ to be true in order for the biconditional statement to be true. This is why we only see a true value when both $P$ and $Q$ are true.

Let us now consider a more complex example of a truth table and how we combine the fundamental rules of logic to a complex set of propositions.

Example:

Consider the proposition $P\vee \neg(P \wedge Q)$ . We construct the following truth table.

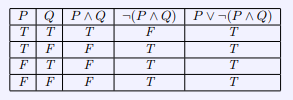
We can see from this example that there are times that, given the placement and negation of certain propositions, we can create a statement that will always be true no matter the truth value of the propositions involved. This can be done through understanding the effects of logical negation on conjunctions and disjunctions. We can see from this example that, by negating a conjunction, it will follow that the truth values of the conjunction will be negated and thus we see opposite truth values between the conjunction and negated conjunction. From here we know that a disjunction only needs the true value from one statement in order for the disjunction to be true. We can see from our table that we have created truth tables for $P$ and $\neg(P \wedge Q)$ that align in such a way that the disjunction will always be true.

This section should include the basics of logic, including truth tables for implications, disjunctions, and conjunctions as well as some challenging logic problems.

9.1 DeMorgan’s Laws

DeMorgan’s laws expand on logic by having a broader realm of applications. Logic only applies to propositions where as DeMorgan’s Laws can apply to sets, elements, and even expressions of numbers. For this introduction, we will define DeMorgan’s Laws using logic notation. We define DeMorgan’s Laws as follows [39].

Theorem:

Let $A$ and $B$ represent two finite sets then

Law of Unions: $\neg(A \vee B) \Leftrightarrow \neg A \wedge \neg B$
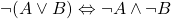
Law of Intersection: $\neg (A \wedge B)\Leftrightarrow \neg A \vee \neg B$

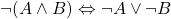
We can see how DeMorgan’s law distributes the negation, or denial, over the collection of propositions. This idea can be applied to sets as well, which we will study in depth later on. Looking back we have actually already applied DeMorgan’s law to a logic problem before but we will now look at an example that will help to solidify this understanding of the equality for each law.

Example:

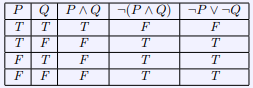
Here we have an example of a truth table that utilizes DeMorgan’s law for conjunction. We can see with this truth table, the equality between $\neg (P\wedge Q)$ and $\neg P \vee \neg Q$ . This supports DeMorgan’s law that $\neg (A \wedge B)\Leftrightarrow \neg A \vee \neg B$ . What we can see implied by DeMorgan’s law is that if $\neg(P \wedge Q)$ is true the it is true only if $\neg P \vee \neg Q$ , and vice verse. We see this same idea applied in the next example as well, this time constructing a truth table for DeMorgan’s law of unions.

Example:

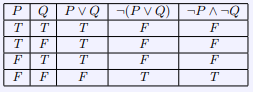
In this example we again see that the truth values for $\neg(P \vee Q)$ and $\neg P \wedge \neg Q$ are the same. This would support DeMorgan’s law that $\neg(A \vee B) \Leftrightarrow \neg A \wedge \neg B$ . It is implied, here, that $\neg(P \vee Q)$ cannot be true unless $\neg P \wedge \neg Q$ is true, and $\neg P \wedge \neg Q$ cannot be true unless $\neg(P \vee Q)$ is true.

There are many subjects in math that DeMorgan’s laws can be applied to. Consider a basic expression as an example, when we have an addition problem $2x+4$ . Consider “+” to represent the union of $2x$ and $4$ and when we negate the expression we find $-(2x+4)=-2x-4$ . We can see now that we have an intersection where we are now set to find the difference between $-2x$ and $4$ .

We can even relate DeMorgan’s laws to the discussion of proofs. Techniques like contraposition sometimes involve taking a claim that involves two parts and negating the claim to then solve and conclude the findings. We will shed more light on these techniques in the next sections.

10 Logic

License

Share This Book