19 Axioms or Real Analysis
We have known about addition and multiplication for years. In real analysis we cover the axioms for addition and multiplication. Axioms are the established propositions or fundamental rules that surround addition and multiplication. In algebra and arithmetic we simply exercised numbers through functions simply knowing they would lead to certain values. Lets look at the different axioms, or field axioms, for addition and multiplication [39].
16.1 Field Axioms
Commutative Law for Addition: ![]()
Associative Law for Addition: ![]()
Existence of Additive Identity: ![]()
Existence of Additive Inverse: ![]()
Associative Law for Multiplication: ![]()
Existence of Multiplicative Identity: ![]()
Existence of Multiplicative Inverse: ![]() for
for ![]()
Commutative Law for Multiplication: ![]()
Distributive Law: ![]()
We can look at this list and see hundreds of math problems that we have most likely solved because of these axioms. Now there is another way to write the distributive law but we have not included it here because the commutative law for multiplication validates it’s equality to the distributive law for addition that we have been given. We have actually already established an understanding of the distributive law as it was used in DeMorgan’s law in the form of the distribution of negation over the union or intersection of two propositions, as well as some of our subset proofs. With the idea of relations in mind lets delve into ordered field axioms.
16.2 Order Axioms
We have seen real numbers have greater, less than, and equal values which is why there are fundamental axioms for these as well.
Trichotomy: If ![]() , then only one of the following can be true:
, then only one of the following can be true: ![]() ,
, ![]() ,
, ![]() .
.
We all, usually, have an unknowing mastery of trichotomy but in real analysis we acknowledge that there is a fundamental principal for the relationship between strict inequalities and equality. We take this understanding and put it into the axiom Trichotomy. We know that an element strictly smaller or larger than another cannot be equal and vice versa. It is also known that an element that is smaller cannot also be larger, thus concluding the trichotomy axiom. The remaining axioms we will list below [21].
- Let
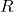 represents the set of all positive numbers. If
represents the set of all positive numbers. If 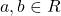 , then
, then 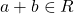 .
. - Let
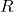 represent the set of all positive numbers. If
represent the set of all positive numbers. If 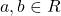 , then
, then 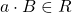 .
. - For all
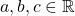 , if
, if 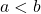 then
then 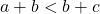 .
. - For all
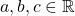 , if
, if 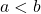 and
and 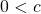 then
then 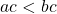 .
.
There is another axiom we have not included in here because it has already been defined but that is the transitivy axiom mentioned in our section on functions.
Now that we have established relationships full circle and know how to implement them and understand the abstract rules behind them let’s address one theorem that utilizes order axioms, the Triangle Inequality theorem.
Theorem: Triangle Inequality
Any side of a triangle is always shorter than the sum of the other two sides.
This is a fundamental definition for a triangle, by this we mean no the related sides can come to together to create a triangle without begin in accordance with the triangle inequality. Rightly so, in order for a geometric shape to be a triangle the sum of the lengths of any two sides is greater than the length of the third side. Each of the following inequalities must be met [1].
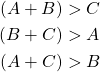
Now if one or more of these inequalities are not satisfied then the three sided object is, in fact, not a triangle. We could look at an object with three sides and unless the sides fall under the requirements of the triangle inequality then no matter what combination of angles and sides are attempted, a triangle cannot be formed.
We can also use the triangle inequality to find the missing side length of a triangle. Lets consider an example.
Example:
Consider the triangle with given side lengths ![]() and
and ![]() . Using the triangle inequality theorem find the length of side
. Using the triangle inequality theorem find the length of side ![]() .
.
First we let
![]()
By the triangle inequality ![]() .
.
Consider ![]() if we subtract
if we subtract ![]() from both sides we get the inequality
from both sides we get the inequality ![]() which simplifies to
which simplifies to ![]() .
.
Lastly, if ![]() then by subtracting
then by subtracting ![]() from both sides we get
from both sides we get ![]() which simplifies to
which simplifies to ![]() . This is invalid because side lengths cannot be negative. Thus the side length of
. This is invalid because side lengths cannot be negative. Thus the side length of ![]() is
is ![]() and with this we conclude the proof.
and with this we conclude the proof.
It may seem that the example ended a bit abruptly but the idea behind using the triangle inequality theorem to find the side length of a triangle with the desired result of finding an exact side length but a range of side lengths that will satisfy the triangle under the theorem.
To summarize, the axioms covered describe the structures and relationships of real numbers. Using axioms we can define structures on a set which leads us to the topology of real numbers discussed in the next section.
