4 Integrals
Simply put an integral generates the area under a curve on the interval ![]() . There are many different ways to calculate the area under a curve. Examples include right, left, and mid-point approximations. Using the area of smaller rectangles to roughly summarize the total area underneath the curve for
. There are many different ways to calculate the area under a curve. Examples include right, left, and mid-point approximations. Using the area of smaller rectangles to roughly summarize the total area underneath the curve for ![]() to
to ![]() either by left, right, or mid-hand points, this type of approximation is known as Riemann sums. The fault of this kind of calculation is that it requires
either by left, right, or mid-hand points, this type of approximation is known as Riemann sums. The fault of this kind of calculation is that it requires ![]() to be continuous and non-negative [35]. This is where definite integrals have the upper hand,
to be continuous and non-negative [35]. This is where definite integrals have the upper hand, ![]() need not be continuous and non-negative in order for integration to be able to calculate the area under the curve for
need not be continuous and non-negative in order for integration to be able to calculate the area under the curve for ![]() . The formal definition is as follows [35].
. The formal definition is as follows [35].
Definition.
Given ![]() is a function defined on the interval
is a function defined on the interval ![]() , then the definite integral of
, then the definite integral of ![]() from
from ![]() to
to ![]() is denoted by
is denoted by
![]()
In the following graph we are given the line for the function ![]() . On the interval from (2,4) we have a shaded region between the curve and the x-axis. This shaded region is what we are solving for when we evaluate an integral.
. On the interval from (2,4) we have a shaded region between the curve and the x-axis. This shaded region is what we are solving for when we evaluate an integral.

Given this formal definition we can now introduce the Mean Value theorem [35].
Theorem: The Mean Value Theorem
If ![]() is continuous on the interval
is continuous on the interval ![]() , then there is a
, then there is a ![]() such that
such that
![]()
The objective of an integral is to anti-differentiate and solve for the function ![]() an interval
an interval ![]() . This is part one of the Fundamental Theorem of Calculus [35].
. This is part one of the Fundamental Theorem of Calculus [35].
Theorem: Fundamental Theorem of Calculus, Part 1
If ![]() is a continuous function on
is a continuous function on ![]() , then the function
, then the function ![]() is defined by
is defined by
![]() ,
, ![]() such that
such that ![]() on
on ![]() .
.
Consider an example involving this theorem.
Example:
Given the integral ![]() , by the fundamental theorem of calculus
, by the fundamental theorem of calculus ![]() .
.
The second part of the Fundamental Theorem of Calculus gives the formal definition for finding the area of a region with only the end points of the interval [35].
Theorem: Fundamental Theorem of Calculus, Part 2
If ![]() is continuous on the interval
is continuous on the interval ![]() and
and ![]() is the anti-derivative of
is the anti-derivative of ![]() , then
, then
![]()
This may be considered one of the most important theorems in mathematics, as it allows us to quantify areas that may take many humans lifetimes to calculate if at all possible.
We will now proceed to the rules of integration, it should be noted that these rules bare many similarities to the rules given for differentiation. We begin with some of the most common integrals. As well, the constant ![]() added to every integration solution is the unknown constant of the anti-derivative that needs to be considered because when
added to every integration solution is the unknown constant of the anti-derivative that needs to be considered because when ![]() , containing constant
, containing constant ![]() , is differentiated
, is differentiated ![]() per the constant rule.
per the constant rule.
Constants
Let ![]() where
where ![]() is a constant. The integral for
is a constant. The integral for ![]() is written as
is written as
![]()
Given the rule of constants under integration [37], we see we are, in a way, undoing the work of differentiation. Just as we took the derivative of ![]() to find
to find ![]() . Under the constant rule for integration if
. Under the constant rule for integration if ![]() then
then ![]() , for
, for ![]() .
.
Variables
Consider ![]() , by the integration of variables
, by the integration of variables
![]()
Under the rule for variables [37], we are essentially reversing the work of derivatives. This rule stands as a definition for the behavior of a variable as it undergoes integral evaluation. The next few rules are more definitions for the behavior of variables under different operations.
Reciprocals
Let ![]() , then we write the integral as
, then we write the integral as
![]()
Here we can see that if we have a function that bares strong resemblance to ![]() , or a function that can be simplified to the format, then we can apply the reciprocal rule to evaluate the integral [37]. To best understand this law we can look at an example.
, or a function that can be simplified to the format, then we can apply the reciprocal rule to evaluate the integral [37]. To best understand this law we can look at an example.
Example:
Given ![]() , evaluate the integral for
, evaluate the integral for ![]() .
.
Per the Rule for reciprocals we start with the following integral and then move to simplify the integral by moving the ![]() outside of the integral.
outside of the integral.
![]()
Now, we can move to integrate ![]() using our rule of reciprocals.
using our rule of reciprocals.
![]()
Thus we can see how a function ![]() of this format behaves under integration.
of this format behaves under integration.
Exponents
Let ![]() ,
, ![]() .
.
Now if we had a constant ![]() such that
such that ![]() then we can integrate
then we can integrate ![]() as follows [37].
as follows [37].
![]()
What we see from this integration that, just as the derivative of ![]() resulted in
resulted in ![]() the antiderivative is thus
the antiderivative is thus ![]() . The only exception is when there is a operations on
. The only exception is when there is a operations on ![]() . If
. If ![]() has been multiplied by a constant or hase been put to the power of some
has been multiplied by a constant or hase been put to the power of some ![]() then we must integrate the exponent as though we were taking the antiderivative with respect to x, utilizing integration behavior of the operations on
then we must integrate the exponent as though we were taking the antiderivative with respect to x, utilizing integration behavior of the operations on ![]() .
.
The Power Rule
Let ![]() for
for ![]() , by the power rule [37]
, by the power rule [37]
![]()
Again, the rules are meant to provide structure for how functions of a defined format are to behave under integration. The power rule provides an axiom for how a function with exponent ![]() will perform under integration.
will perform under integration.
The Constant Rule
Let ![]() be a constant then the integral for
be a constant then the integral for ![]() is as follows [37]:
is as follows [37]:
![]()
As we can see from this definition the constant rule shows us that a constant multiple is not affected by an integral, it can be extracted from the integral and then multiplied to the result of the integral. In many cases we use this rule as a step to simplify the integral before evaluating.
The Sum Rule
Consider ![]() and
and ![]() , by the sum rule for integration [37]. The integral of
, by the sum rule for integration [37]. The integral of ![]() is
is
![]()
Just as we differentiated functions independently of one another when they were brought together under addition, the same is true for integration. There is nothing fancy about the integration of a function ![]() , with multiple functions added together, to create
, with multiple functions added together, to create ![]() . Thus when we integrate we can do so in one or separately but the results will be equal to one another.
. Thus when we integrate we can do so in one or separately but the results will be equal to one another.
The Difference Rule
Again consider the functions ![]() and
and ![]() , by the difference rule [37] the integral for
, by the difference rule [37] the integral for ![]() is
is
![]()
As we mentioned in the sum rule for integration the same can be said for the difference rule. If we have a function ![]() , made up of the difference between smaller functions, then we can either integrate
, made up of the difference between smaller functions, then we can either integrate ![]() under one integral or we can separate them as a way to simplify the integration. Either way the result will be the same.
under one integral or we can separate them as a way to simplify the integration. Either way the result will be the same.
Integration by Parts
We will briefly cover integration by parts [35] here as an introduction but will delve deeper in a later section. Integration by parts is utilized when ![]() contains two functions multiplied together. Let
contains two functions multiplied together. Let ![]() and
and ![]() be independent functions such that
be independent functions such that
![]()
Integration by parts is vastly more complex than the basic rules we have covered thus far. This integration method utilizes the integration rules listed previously depending on the variables ![]() and
and ![]() . In mathematics, many times we are required to recognize the format of various functions in order to distinguish which method we will be applying to integrate the function. Integration by parts is also unique in that it, at times, my require many rounds of integration depending on the structure of
. In mathematics, many times we are required to recognize the format of various functions in order to distinguish which method we will be applying to integrate the function. Integration by parts is also unique in that it, at times, my require many rounds of integration depending on the structure of ![]() and whether it can easily by integrated or if another integration by parts is necessary. Another form of integration, when a function may seem complex enough that it might take hours to properly integrate, is by substitution.
and whether it can easily by integrated or if another integration by parts is necessary. Another form of integration, when a function may seem complex enough that it might take hours to properly integrate, is by substitution.
Integration by Substitution
There are cases where finding the anti-derivative of a function is very complex, this is where substitution comes in. Let ![]() such that
such that ![]() is continuous on the interval
is continuous on the interval ![]() , let
, let ![]() be continuous over the range of
be continuous over the range of ![]() with
with ![]() [35]. Then
[35]. Then
![]()
To better explain the process of integration by substitution we are given the following steps to solve the integral [35].
- Select the expression such that
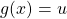 and find
and find 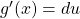 .
. - Now substitute
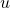 and
and 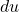 into the integral for
into the integral for 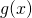 and
and 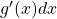 , respectively.
, respectively. - Evaluate the integral with respect to
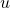 .
. - Once the integral has been evaluated rewrite the solution in terms of
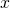 by substituting
by substituting 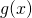 back in for
back in for 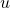 .
.
We will continue the discussion of integration by substitution in regards to trigonometric functions later on in this section.
4.1 Integration by Parts
For every derivative there is an anti-derivative and as such there needs to be a method of integration to anti-differentiate a derivative found by the product rule of differentiation. This is where integration by parts can be introduced. The formal definition was given in the previous section as
![]()
Breaking this definition down, if we consider a function ![]() , by the product rule of differentiation,
, by the product rule of differentiation, ![]() [35]. We now need to anti-differentiate with respect to
[35]. We now need to anti-differentiate with respect to ![]() . Using integration by parts we have
. Using integration by parts we have
![]()
Here we can actually apply the sum rule for integration
![]()
Now given that integration is finding the anti derivative we can set the integral equal to ![]() and solve for
and solve for ![]() [35].
[35].
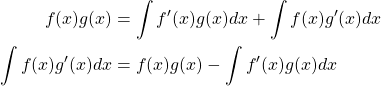
Now, if we replace ![]() and
and ![]() with
with ![]() and
and ![]() respectively we get our formal definition.
respectively we get our formal definition.
![]()
Let us consider some examples of this technique in application.
Example:
Consider the integral ![]() let
let ![]() and
and ![]() such that
such that ![]() . By integration by parts we can rewrite the integral and solve.
. By integration by parts we can rewrite the integral and solve.
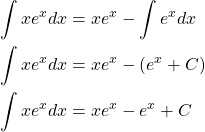
Thus by integration by parts we have found ![]() .
.
4.2 Trigonometric Substitution
We briefly introduced substitution in a previous section but will now continue with substitution with trigonometric functions. It is vital to know how to use trigonometric functions to substitute for expressions when integrating certain functions. Knowing the following substitutions and how to evaluate them will make integrating complex expressions involving the roots of quadratics far easier. Consider the three important trigonometric substitutions for integration [35].
- Consider the expression
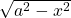 , then we let
, then we let 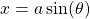 such that
such that
![]()
- Consider the expression
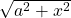 , then we let
, then we let 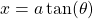 such that
such that
![]()
- Consider the expression
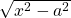 , then we let
, then we let 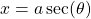 such that
such that
![]()
Let us now visit an example to show how trigonometric substitution is applied and follows through after evaluation.
Example:
Given the integral
![]()
We instantly see from the expression in the denominator that ![]() such that
such that ![]() and
and ![]() . Let us now substitute these new found expressions back into the integral and evaluate.
. Let us now substitute these new found expressions back into the integral and evaluate.
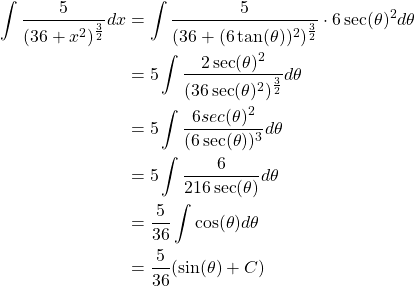
Now that we have evaluated the integral we must convert the solution back into terms of ![]() . We know
. We know ![]() such that
such that ![]() .
.
Consider a triangle then, with opposite side to the hypotenuse as ![]() and adjacent side to the hypotenuse as
and adjacent side to the hypotenuse as ![]() , then the hypotenuse is
, then the hypotenuse is ![]() .
.
Let ![]() be equivalent to the opposite side over the hypotenuse resulting in
be equivalent to the opposite side over the hypotenuse resulting in ![]() . Then substitute this expression of
. Then substitute this expression of ![]() for
for ![]() and simplify.
and simplify.
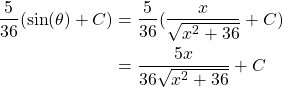
Thus we have found through trigonometric substitution that
![]()
The following video offers a deeper look at integration by parts and trigonometric substitution, two of the more challenging integration methods. At the end of the video we will also be introduced to a real world application of integration.
