43 Game Theory
In our previous discussion on decision theory we were introduced to models with outcomes and payoffs solely dependent on one person’s decisions, in game theory we have to take into account multiple players’ choices. In mathematical modeling we split game theory into two categories, total conflict and partial conflict games. We begin with total conflict, wherein we have pure or mixed strategy.
Total Conflict
If we have a total conflict game with pure strategy then we are saying there is a deliberate course of actions a player can make to reach a desired outcome. When we consider strategies we need to look for dominant strategies [9].
Definition.
A strategy 
dominates a strategy 
if every outcome in is at least as good as the corresponding outcome in and at least one outcome in is strictly better than the corresponding outcome in .
What this means is that in order for us to say there is a dominant strategy the strategy should have no outcome less than the outcomes of another strategy. As well the supposed dominant outcome must hold an outcome that is strictly better than the corresponding outcome in another strategy. Consider the below problem.
Examples
Example:
Determine whether the following zero-sum game has a pure strategy. Assume the row player is maximizing their payoff [9].
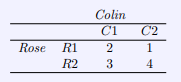
Here we know Rose is trying to maximize her payoff she can either use strategy 
or 
, while Colin wants to minimize his losses by either choosing 
or 
. From the table we can see that if Rose plays and Colin plays then Rose wins. We can then say that the value of the game is 
.
We were able to come to this conclusion because we looked at Rose’s options, the values in are not maximizing her payoff because has better value no matter which option Coin takes. Once we commit to then it is up to Colin to choose the best option to minimize his losses. Since 
, Colin will choose .
This example leads us to introduce a Nash equilibrium [9].
Definition.
A Nash equilibrium is an outcome where neither player can benefit by departing unilaterally from its strategy associated with that outcome.
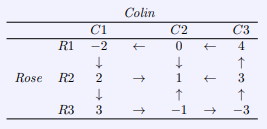
This means that no player in the game can benefit by straying from their strategy if the opposing player does not also change their strategy. Looking back at our previous example we see that we have a pure strategy Nash equilibrium, as illustrated by the movement diagram.
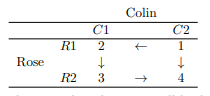
This illustration shows us that the arrows all lead to 
and thus we can say that this example was a pure strategy Nash equilibrium. Now that we have a handle on total conflict, pure strategy games we move to total conflict, mixed strategy games.
Definition.
A mixed strategy is a particular randomization over a players pure strategies. Each of the players pure strategies is assigned some probability indicating the relative frequency with which the pure strategy will be played.
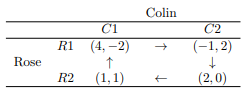
This table is a mixed strategy because if Rose chooses to go for the best possible option, , then Colin will choose and Rose will hurt. Meanwhile, if Rose chooses to intentionally hurt herself by choosing then Colin will choose to minimize his losses and go for . Either way the result is one player will be hurt by the other players desire to improve their payoff. This leads us to the discussion of partial conflict [9].
Partial Conflict
Definition.
If for each possible outcome the payoffs to each player do not sum to the same constant, the game is classified as partial conflict.
Essentially we are saying if both players can attempt for the best outcome for themselves, without hurting the other than we have a partial conflict. We can look at fair deals as partial conflicts, if communication is made and both players agree to a strategy that will benefit both or both players agree to take a hit for the best outcome for both parties then we have a form of partial conflict. Now there are three scenarios within a partial conflict game: with communication, without communication, with an arbiter. What we just considered was a partial conflict with communication or more likely with arbiter, as an arbiter’s role is to help negotiate a fair agreement between parties.
A well know example of a partial conflict is the “Prisoner’s Dilemma”.
Example:
The police have arrested two suspects of a large crime, each suspect has the same options. Each can either confess or not. The prosecutor only has enough evidence to convict both suspects on minor charges, so he is looking for a confession to the larger crime. The minor offense carries a 1 year sentence whereas the larger crime has 20 years. The suspects can’t communicate and are both told if one confesses then the one can go free while the other will receive 20 years. If both confess then the sentence for both will be only 5 years [9].
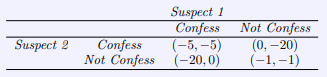
We see that each suspect has a dominant strategy, if Suspect 1 confesses and Suspect 2 does not then Suspect 1 is free and Suspect 2 is sentenced to 20 years and vice versa. These two strategies conflict with one another. If we map the movement we get the following.
In this example the Nash equilibrium is represented by the scenario in which both suspects confess. Either way if Suspect 1 confesses and Suspect 2 does not then Suspect 1 goes free but if Suspect 2 confesses as well then they both only get 5 years and vice versa. Now the best option is that both should keep quiet as they both get the best outcome from this strategy, this goes against the Nash equilibrium but for the two suspects it provides the best outcome possible without communication.
Now that we have covered total and partial conflict, as well as observed examples of pure and mixed strategy, we can begin to discuss alternative ways to solve for the best strategy. We already know about maximizing payoff and minimizing loss, now we can cover maximin and minimax strategies [9].
Definition.
The maximin strategy is when the minimum value of each strategy is determined and the maximum of the minimum values is selected.
We call it the maximin strategy because we are selecting the corresponding strategy to get the maximum payoff from the minimum options. To counter this strategy we have the minimax strategy.
Definition.
The minimax strategy is when the maximum values of each strategy are determined and the minimum value of these maximums is selected.
Now when the maximin and minimax values are the same, we call this a saddle point. Let us look at an example.
Example:
Given the following table, find all the pure strategy solutions [9].
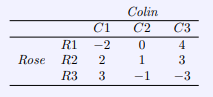
We apply the same goals for Rose and Colin as before. Rose wants to maximize her payoff and Colin wants to minimize his losses. Using the minimax and maximin strategy, we will look to find the minimum of the column maximums and also look to find the maximum of the row minimums.
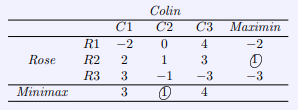
We see we have a saddle point of 
which equates to the value of the game. Thus Rose has a winning strategy in and Colin’s winning strategy is . If we look at a movement diagram we can see that 1 is the Nash equilibrium value because no arrows point outwards from 1 and thus we have a pure strategy.
The examples that we have been looking at are mostly games, but game theory has a very real role in our world. Countries in the middle of war, agreements between companies, and settling boycotts can all use game theory. In the following example we will look at a disagreement between a company and its workers, using game theory we will be able to tell if a peaceful settlement is possible.
Example:
A writers guild is on strike because of frustration over wages. The strike has gone on long enough that currently the movie industry has lost over 
billion dollars. Management has threatened that they will not consider negotiations until the strike has stopped. The payoff matrix is as follows.
Where 
is to strike, 
is not strike, 
is to keep the status quo, and 
is to increase salaries and revenue sharing [9].
Without communication we can see the Nash equilibrium is 
and thus if both players move to maximin their strategy then the outcome is most likely .
If there was communication, from the Writers Guild perspective:
If the Writers Guild moves first and chooses to strike, , then management will choose the status quo, , which implies is the result.
If the Writers Guild chooses not to strike, , then management will still choose the status quo, , resulting in 
. This is not worth anything to the Writers Guild for the purpose of this argument, thus the Writers Guild will choose the strategy of moving to strike first.
If the Writers Guild forces Management to move first:
If Management chooses to keep the status quo, , then the Writers Guild will choose to strike, , resulting in .
If Management chooses to increase salary, , then the Writers Guild will not strike, , and the result will be 
. This is not worth anything to Management as they stand to lose and thus Management would choose to keep the status quo.
If the Writers Guild moves to threaten Management:
If the Writer’s Guild threatens Management by telling Management they will strike if the status quo is chosen, this is bad for Management but the option to increase salary is worse for them. Thus Management would not choose to accept the threat.
There is an alternative, to make a promise. There is no promise that the Writers guild could make that would motivate Management without hurting themselves, thus no chance for a promise. Therefore we can conclude this is a pure strategy scenario with a Nash equilibrium of .
Having a good understanding of strategy can help anyone placed in a position like those in our example. Scenarios, like the one in our example, have occurred for centuries and have made our world what it is today. We can even consider strategy as it may effect our predator-prey model, when we consider game theory in negotiations between pipeline companies and wildlife conservationist groups.