13 Set Theory
Bridge to Abstract Math, for some, is a very challenging course in mathematics. In previous classes such as calculus, differential equations, and statistics, although we learned abstract theorems, we applied them to problems or real world situations where variables were given finite values. With abstract math we have to prove problems abstractly which means very few finite values, if any, in order to prove the problem for every possible value of a variable. In this course much of what we learn to create proofs for are theorems.
Now a theorem cannot prove itself and in this class you are taught to utilize related theorems, axioms, definitions, and proof techniques in order to prove a theorem to be true. Not only did this mean that students needed to learn how to recognize the relationship between numerous definitions, rules, and logical propositions efficiently but the class also teaches students to be concise in developing proofs.
With every proof we needed to provide the key points that would lead to a sound conclusion. This requires students to learn how to clean up proofs as well as how to present information neatly in a proof process, structured by logic and proof techniques, that flows smoothly to a strong conclusion, founded by established axioms and definitions.
In the following subsections we introduce some of the topics discussed in the course Bridge to Abstract Mathematics. This includes set theory, relations, functions, and cardinality. We begin with set theory.
Set theory, as it suggest, discusses the many theorems for sets. We touched briefly on sets early on in this chapter but for a quick review a set is by definition “a well-determined collection of objects that are called elements of the set” [7]. When we study pure set theory we are only discussing theorems for sets whose elements are also sets which means the sets are infinite. Let us consider the operations involved with sets.
Union and Intersection
We have already introduced the union and intersection of sets in the section on DeMorgan’s laws but we will cover them again. The union of two sets, denoted by “![]() “, is when we combine two sets into one set that contains all the elements of both sets. The intersection of two sets is denoted by “
“, is when we combine two sets into one set that contains all the elements of both sets. The intersection of two sets is denoted by “![]() “, which creates a set that only contains like elements. We explained this earlier but for the union, given sets
“, which creates a set that only contains like elements. We explained this earlier but for the union, given sets ![]() and
and ![]() , if
, if ![]() or
or ![]() then
then ![]() and for the intersection this means if
and for the intersection this means if ![]() then it must be that
then it must be that ![]() and
and ![]() .
.
Now union and intersection do not always involve only two sets. We can denote the union of more than two sets as the following [7].
![]()
We can see here in the notation that the sets are denoted ![]() for with the first set being
for with the first set being ![]() . Using this same notation for the sets we see the formal notation for intersection of more than two sets as the following [7].
. Using this same notation for the sets we see the formal notation for intersection of more than two sets as the following [7].
![]()
Let’s now consider some basic examples for the union and intersection of sets.
Example:
Let set ![]() and let set
and let set ![]() then then union of sets
then then union of sets ![]() and
and ![]() is
is
![]()
Here we see that the union of sets ![]() and
and ![]() results in a set with all values of both set
results in a set with all values of both set ![]() and
and ![]() .
.
The intersection of ![]() and
and ![]() would be as follows
would be as follows
![]()
Results in a set which only contains the elements that are shared between ![]() and
and ![]() .
.
We can see a key aspect of union in the example above, when we combined the two sets we only accounted for like elements once. This also holds for a union of more than two sets as well. In the intersection we saw that the only elements for the intersection of sets ![]() and
and ![]() were elements {1} and {6}, this is because these are the only elements that are contained in both sets independently. We can see an image below illustrating the intersection of two sets below.
were elements {1} and {6}, this is because these are the only elements that are contained in both sets independently. We can see an image below illustrating the intersection of two sets below.
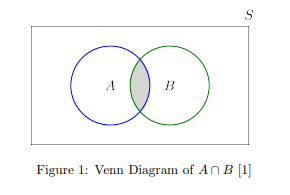
Now consider some slightly more complex operations of sets.
Complement of Sets
Consider that we have a universal set ![]() , let
, let ![]() be a set within
be a set within ![]() . Now set
. Now set ![]() does not contain all elements of the universal set, just a cluster of elements. All other elements are contained in what we call the compliment to set
does not contain all elements of the universal set, just a cluster of elements. All other elements are contained in what we call the compliment to set ![]() , denoted as
, denoted as ![]() . It follows then that if
. It follows then that if ![]() but
but ![]() then it must be that
then it must be that ![]() , as well if
, as well if ![]() and
and ![]() then it must be that
then it must be that ![]() .
.
Difference of Sets
We discussed the intersection of sets already but the difference of sets is very close to the opposite of intersection. Similar but not the same though, as intersection only included the shared elements between overlapping sets, a difference is what does not over lap, in a way. Consider sets ![]() and
and ![]() again, the difference of sets is the resulting set from
again, the difference of sets is the resulting set from ![]() or
or ![]() . This essentially means if
. This essentially means if ![]() then the resulting set contains all elements other than elements only in
then the resulting set contains all elements other than elements only in ![]() and shared between
and shared between ![]() and
and ![]() . Consider the example below.
. Consider the example below.
Example:
Let ![]() and let
and let ![]() the difference of
the difference of ![]() is the following
is the following
![]()
Vice versa then difference of ![]() is the following
is the following
![]()
We see in the above example that we only focus on the elements contained in the set being subtracted from. What this means is that any elements in the set on the right hand side of the subtraction symbol are not included in the resulting set, they are excluded as well as any elements shared between the sets. Now lets look at sets that carry no association at all.
Disjoint Sets
Recall complimentary sets and the universal set ![]() . Now imagine that just as
. Now imagine that just as ![]() only contains a few elements of
only contains a few elements of ![]() , there is another set
, there is another set ![]() that contains a few other elements of
that contains a few other elements of ![]() such that for every
such that for every ![]() ,
, ![]() and vice versa. Furthermore we can have yet another set
and vice versa. Furthermore we can have yet another set ![]() that contains a few other elements not shared with either
that contains a few other elements not shared with either ![]() or
or ![]() . These are all examples of disjoint sets. They contain no mutual elements which makes them mutually exclusive to one another. With this being said the intersection set between any or all disjoint sets in
. These are all examples of disjoint sets. They contain no mutual elements which makes them mutually exclusive to one another. With this being said the intersection set between any or all disjoint sets in ![]() is an empty set. Consider the below example.
is an empty set. Consider the below example.
Example:
Let ![]() , let disjoint sets
, let disjoint sets ![]() and
and ![]() by definition of disjoint sets there is no element in
by definition of disjoint sets there is no element in ![]() that is also contained in
that is also contained in ![]() and as such the intersection of
and as such the intersection of ![]() and
and ![]() is as follows.
is as follows.
![]()
We continue to expand on the idea of disjoint sets in the next classification.
Partition of Sets
We have a collection of nonempty sets under the universal set ![]() again, where each set is disjoint and contains some elements of
again, where each set is disjoint and contains some elements of ![]() such that there is no elements
such that there is no elements ![]() that is not contained in some disjoint set
that is not contained in some disjoint set ![]() . We can say that each
. We can say that each ![]() is a partition of
is a partition of ![]() if
if ![]() . Consider an example using the universal set
. Consider an example using the universal set ![]() from disjoint sets.
from disjoint sets.
Example:
Let ![]() and contain the following 5 partitions:
and contain the following 5 partitions: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Then by the definition of partitions the union of all partitions is as follows.
. Then by the definition of partitions the union of all partitions is as follows.
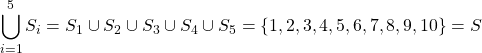
Now that we know how to operate with sets lets consider some of the basic set classification and how it can be used to compare sets.
Subsets
In these last few operations we kept utilizing these sets with universal set ![]() . We can also call these sets subsets. By definition a set which contains every element of another set is therefore a subset of the other set. If
. We can also call these sets subsets. By definition a set which contains every element of another set is therefore a subset of the other set. If ![]() is a subset of
is a subset of ![]() then we can denote this relationship by
then we can denote this relationship by ![]() or
or ![]() .
.
![]() denotes when every element in
denotes when every element in ![]() is in
is in ![]() while
while ![]() denotes when every element in
denotes when every element in ![]() is in
is in ![]() but there are far more elements not in
but there are far more elements not in ![]() that are in
that are in ![]() ; we call this a proper subset. Let us look at an example utilizing a few set operations.
; we call this a proper subset. Let us look at an example utilizing a few set operations.
Example:
For any sets ![]() and
and ![]() prove that
prove that ![]() .
.
Proof: Let there be element ![]() such that
such that ![]() then by the definition for the difference of sets
then by the definition for the difference of sets ![]() and
and ![]() . Thus by the definition of subsets
. Thus by the definition of subsets ![]() .
.
This was quite a simple example and easily proven by definitions. Before we move on to set equality consider one more example of subset relations.
Example:
For all sets ![]() ,
, ![]() , and
, and ![]() if
if ![]() and
and ![]() then
then ![]() [20].
[20].
Proof: Assume ![]() ,
, ![]() , and
, and ![]() are sets such that
are sets such that ![]() and
and ![]() . Let
. Let ![]() be an arbitrary element where
be an arbitrary element where ![]() . Given that
. Given that ![]() then every element in
then every element in ![]() is an element in
is an element in ![]() , thus we can conclude that
, thus we can conclude that ![]() . As such, since
. As such, since ![]() then every element in
then every element in ![]() is an element in
is an element in ![]() , thus
, thus ![]() . Now, since we have proven that every element in
. Now, since we have proven that every element in ![]() is an element in
is an element in ![]() , we can conclude that
, we can conclude that ![]() .
.
We have seen how sets can be related by introducing the definition of a subset. We will now prove how two different sets can be equal to one another using our definition for subsets.
Example:
Let set ![]() and set
and set ![]() . Prove
. Prove ![]() .
.
Proof: Consider ![]() , then by the definition of
, then by the definition of ![]() ,
, ![]() for some
for some ![]() . If
. If ![]() then, for set
then, for set ![]() ,
, ![]() and thus we can say that
and thus we can say that ![]() for some
for some ![]() . Thus we can conclude that
. Thus we can conclude that ![]() and therefore
and therefore ![]() . Now consider that
. Now consider that ![]() , then by definition of
, then by definition of ![]() ,
, ![]() for some
for some ![]() . If
. If ![]() then, for set
then, for set ![]() ,
, ![]() and thus we can say that
and thus we can say that ![]() for some
for some ![]() . Thus we can conclude that
. Thus we can conclude that ![]() and therefore
and therefore ![]() .
.
Since we have proven that ![]() and
and ![]() we can conclude that
we can conclude that ![]() .
.
Now that we have established subsets and set equality we can continue on to some fundamental theorems for sets.
DeMorgan’s Laws
We already discussed DeMorgan’s laws earlier on but we will brush up on them here. There are two laws, both of which apply to sets. We considered the laws before but only with two sets. Since DeMorgan’s laws are applicable to larger collections of sets as well we can denote them, with a slight adjustment, below.
Theorem: DeMorgan’s Laws
Let ![]() be a universal set with
be a universal set with ![]() subsets, by DeMorgan’s Laws
subsets, by DeMorgan’s Laws
Having already summarized DeMorgan’s laws we will now quickly look at some applications with more than two sets before moving on to the next theorem.
Example:
Consider sets ![]() and
and ![]() and the universal set
and the universal set ![]() . Using DeMorgan’s law for the negated union of sets solve for
. Using DeMorgan’s law for the negated union of sets solve for ![]() .
.
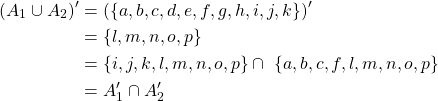
Thus ![]() .
.
In this last example we see that by negating the union of sets ![]() and
and ![]() we are essentially finding the complementary set to the union of
we are essentially finding the complementary set to the union of ![]() and
and ![]() which is the same as if you were to find the intersection for the complementary sets for
which is the same as if you were to find the intersection for the complementary sets for ![]() and
and ![]() .
.
We move on to look at yet another theorem for set theory, the distributive law.
Theorem:
For any sets ![]() ,
, ![]() , and
, and ![]() , by applying the distributive law for sets we have the following:
, by applying the distributive law for sets we have the following:
Just as in arithmetic when we multiplied an entire function by a value or variable by multiplying each element of the function by that value or variable, the same is said for sets. The best way to understand this theorem is by looking at the proofs for these two laws for our examples.
Example:
Prove ![]() .
.
Proof: Let ![]() , then
, then
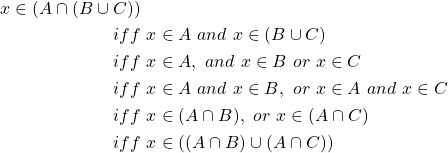
Here we use ![]() to denote “if and only if”. As well, we can note through this work above we use our understanding of elements in relation to unions and intersections of sets to prove
to denote “if and only if”. As well, we can note through this work above we use our understanding of elements in relation to unions and intersections of sets to prove ![]() . We know from previous examples that if a set
. We know from previous examples that if a set ![]() is a subset of a set
is a subset of a set ![]() then every element in
then every element in ![]() is an element in
is an element in ![]() . Thus we utilize this relationship to prove that an arbitrary element in
. Thus we utilize this relationship to prove that an arbitrary element in ![]() is an element in
is an element in ![]() and thus we have proven
and thus we have proven ![]() .
.
Now let ![]() , then
, then
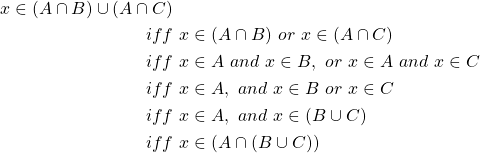
Here we start by looking at an arbitrary element in ![]() and we use this, with our understanding of elements as they relate within unions and intersections of sets to conclude that
and we use this, with our understanding of elements as they relate within unions and intersections of sets to conclude that ![]() is also in
is also in ![]() . Thus proving
. Thus proving ![]() .
.
Since we have proven ![]() and
and ![]() , thus we can conclude that
, thus we can conclude that ![]() .
.
Example:
Prove ![]() .
.
Proof: Let ![]() , then
, then
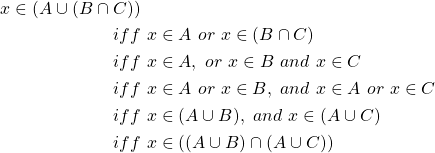
Just as we did in the previous example, we begin with an arbitrary element in ![]() . Through our knowledge of elements as they relate to the union and intersections of sets we draw the conclusion that
. Through our knowledge of elements as they relate to the union and intersections of sets we draw the conclusion that ![]() . Since every element in an arbitrary set
. Since every element in an arbitrary set ![]() is an element in an arbitrary set
is an element in an arbitrary set ![]() if
if ![]() then we draw the conclusion that
then we draw the conclusion that ![]() .
.
Let ![]() , then
, then
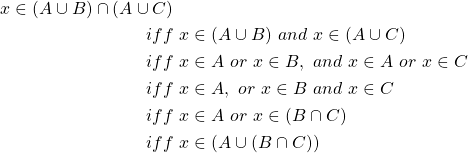
As we did in the previous portion of this example we prove that ![]() and
and ![]() and, since every element in an arbitrary set
and, since every element in an arbitrary set ![]() is an element in an arbitrary set
is an element in an arbitrary set ![]() if
if ![]() then we can conclude that
then we can conclude that ![]() .
.
Since we have now proven that ![]() and
and ![]() then we conclude that
then we conclude that ![]() .
.
Here we can see how by using the definitions for union and intersection we can solve the proofs for the distributive laws by simply following element ![]() as it relates to each set. On the topic of relations we will now progress to the next section covered in the course Bridge to Analysis, relations.
as it relates to each set. On the topic of relations we will now progress to the next section covered in the course Bridge to Analysis, relations.
