14 Set Relations
We have already introduced most common relations in the previous section on logic, where we studied the different symbols and their usage as they related to true and false statements including =, ![]() and
and ![]() . In sets we also looked at the subset and proper subset of sets, denoted
. In sets we also looked at the subset and proper subset of sets, denoted ![]() and
and ![]() , respectively. In this section we will discuss some formal definitions and classifications of relations [38].
, respectively. In this section we will discuss some formal definitions and classifications of relations [38].
Definition.
Let ![]() and
and ![]() be sets. A relation
be sets. A relation ![]() from
from ![]() to
to ![]() is a subset of
is a subset of ![]() . Given an ordered pair
. Given an ordered pair ![]() in
in ![]() ,
, ![]() is related to
is related to ![]() by
by ![]() , written
, written ![]() , if, and only if,
, if, and only if, ![]() is in
is in ![]() . The set
. The set ![]() is called the domain of
is called the domain of ![]() and set
and set ![]() is called its co-domain.
is called its co-domain.
We can also tie in logic since every relation has a true or false value to it as well since ![]() is considered a statement. To have this make more sense, consider that
is considered a statement. To have this make more sense, consider that ![]() is a relation, which we already know, but it should be noted that this means that examples of
is a relation, which we already know, but it should be noted that this means that examples of ![]() can be
can be ![]() ,
, ![]() ,
, ![]() . Thus, we can say that every time we have looked at an example with multiple sets or logical propositions we are looking at relations with
. Thus, we can say that every time we have looked at an example with multiple sets or logical propositions we are looking at relations with ![]() defined as a union, intersection, “if, then” statements, etc.
defined as a union, intersection, “if, then” statements, etc.
Now ![]() has properties that allow us to classify each relation [38].
has properties that allow us to classify each relation [38].
Definition.
Let ![]() be a relation on a set
be a relation on a set ![]() .
.
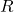 is reflexive if, and only if, for all
is reflexive if, and only if, for all 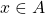 ,
, 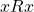 .
.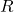 is symmetric if, and only if, for all
is symmetric if, and only if, for all 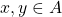 , if
, if 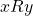 then
then 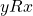 .
.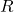 is transitive if, and only if, for all
is transitive if, and only if, for all 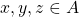 , if
, if 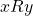 and
and 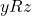 then
then 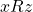 .
.
If we want to classify a relation ![]() as reflexive then for every element
as reflexive then for every element ![]() in the set
in the set ![]() ,
, ![]() must relate to itself. If we want to classify a relation
must relate to itself. If we want to classify a relation ![]() as symmetric then for every element
as symmetric then for every element ![]() and
and ![]() in the set
in the set ![]() , if
, if ![]() is to relate to
is to relate to ![]() then
then ![]() must relate to
must relate to ![]() .
.
Finally, in order for us to classify ![]() as transitive if elements
as transitive if elements ![]() ,
, ![]() , and
, and ![]() are all within set
are all within set ![]() and
and ![]() relates to
relates to ![]() the same way
the same way ![]() relates to
relates to ![]() then
then ![]() should relate to
should relate to ![]() the same as well.
the same as well.
It should be noted that a relation does not need to meet all three classifications to be a relation. There is a kind of relation that does require all three to be met, which we will address later on.
Now there are opposing classifications for relations as well.
Definition.
Let ![]() be a relation on set
be a relation on set ![]() .
.
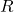 is irreflexive if there is no element
is irreflexive if there is no element 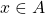 such that
such that 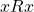 .
.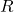 is antisymmetric if for all
is antisymmetric if for all 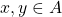 ,
, 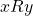 and
and 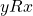 implies
implies 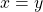 .
.
Now that we have established the characterizations for relations, consider the relation classifications using different orders of the characterizations.
12.1 Ordering Relations
We can consider some classifications for types of relations using different orders of relation characterization.
Definition. Partial Order
Let ![]() be a binary relation on
be a binary relation on ![]() ,
, ![]() is a partial order relation if it is reflexive, anti-symmetric, and transitive.
is a partial order relation if it is reflexive, anti-symmetric, and transitive.
In Bridge to Abstract Mathematics we use a diagram known as the Hasse Diagram to display partial orders. An example of a partial order using a Hasse Diagram can be see below.
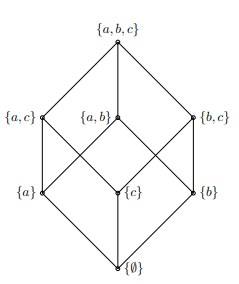
Let us look at an example for proving a partial order relation below.
Example:
Prove that if ![]() is a partial order on a set
is a partial order on a set ![]() , then
, then ![]() , the inverse of
, the inverse of ![]() , is also a partial order on
, is also a partial order on ![]() [20].
[20].
Reflexive: Since ![]() is a partial order let
is a partial order let ![]() such that (
such that (![]() )
)![]() and
and ![]() . Then (
. Then (![]() )
)![]() such that
such that ![]() . We can thus conclude that
. We can thus conclude that ![]() is reflexive on
is reflexive on ![]() .
.
Anti-symmetric: As well since ![]() is a partial order let
is a partial order let ![]() such that
such that ![]() , so
, so ![]() and
and ![]() ,
, ![]() . Therefore
. Therefore ![]() such that
such that ![]() and
and ![]() , thus
, thus ![]() . We can conclude that
. We can conclude that ![]() is anti-symmetric.
is anti-symmetric.
Transitive: Finally since ![]() is a partial order let
is a partial order let ![]() such that
such that ![]() so
so ![]() ,
, ![]() , and
, and ![]() . Therefore
. Therefore ![]() such that
such that ![]() ,
, ![]() and thus
and thus ![]() . We can thus conclude that
. We can thus conclude that ![]() is transitive.
is transitive.
Thus by the definition of partial orders ![]() is a partial order on
is a partial order on ![]() if
if ![]() is a partial order on
is a partial order on ![]() .
.
Continuing on to another ordering relation, Total Order or Linear Order. Before we can introduce this order we need to briefly define the Trichotomy law, also called comparability [39].
Definition. Trichotomy Law
For arbitrary real numbers ![]() and
and ![]() , exactly one of the relations
, exactly one of the relations ![]() ,
, ![]() , or
, or ![]() holds.
holds.
With the trichotomy law essentially tells us that for two real, arbitrary number ![]() and
and ![]() either
either ![]() ,
, ![]() , or
, or ![]() . At no time can
. At no time can ![]() and
and ![]() have more than one of these relations. This means if
have more than one of these relations. This means if ![]() then
then ![]() and
and ![]() , if
, if ![]() then
then ![]() and
and ![]() , and if
, and if ![]() then
then ![]() and
and ![]() .
.
Now that we have established this law we will continue to the formal definition for a Linear Order [39].
Definition. Linear Order
Let ![]() be a binary relation on set
be a binary relation on set ![]() ,
, ![]() is linear, or total order relation if it is a partial order, and for every
is linear, or total order relation if it is a partial order, and for every ![]()
![]() or
or ![]() .
.
The linear order is meant to help mathematicians easily distinguish sets that are partial orders, which we defined previously, and for which every pair of elements ![]() and
and ![]() in the set either have the relation
in the set either have the relation ![]() or
or ![]() but not both. The last order we will cover is the quasi order [4].
but not both. The last order we will cover is the quasi order [4].
Definition. Quasi Order
Let ![]() be a binary relation on
be a binary relation on ![]() ,
, ![]() is a Quasi Order relation if it is irreflexive and transitive.
is a Quasi Order relation if it is irreflexive and transitive.
Again, we have an order that allows us to distinguish sets that only fulfill the irreflexive and transitive properties, which we previously defined. Examples of quasi ordering are proper subsets, where ![]() can be a proper subset of another proper subset but for which
can be a proper subset of another proper subset but for which ![]() cannot be a proper subset of itself. Another example involves less-than relation which is utilized similarly for values of
cannot be a proper subset of itself. Another example involves less-than relation which is utilized similarly for values of ![]() instead of using set relations for a set
instead of using set relations for a set ![]() . Let us now move on to one of the most used and most important ordered relations in abstract mathematics, the Equivalence Relation.
. Let us now move on to one of the most used and most important ordered relations in abstract mathematics, the Equivalence Relation.
12.2 Equivalence Relations
Now we discussed, earlier, that relations do not need to be reflexive, symmetric, and transitive in order to be a relation. There is one kind of relation that does require all three classifications to be met though, the equivalence relation [38].
Definition.
Let ![]() be a set and
be a set and ![]() a relation on
a relation on ![]() ,
, ![]() is an equivalence relation if, and only if,
is an equivalence relation if, and only if, ![]() is reflexive, symmetric, and transitive.
is reflexive, symmetric, and transitive.
Now consider some proofs for finding equivalence relations.
Example:
Prove relation ![]() on
on ![]() , defined by
, defined by ![]() if
if ![]() is even [20].
is even [20].
Proof:
- Reflexive: If
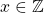 then
then 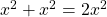 . By definition of even numbers,
. By definition of even numbers, 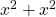 and we can conclude that R is reflexive.
and we can conclude that R is reflexive. - Symmetric: If
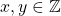 such that
such that 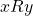 then
then 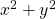 is even. By the commutative law for integers we can also conclude that
is even. By the commutative law for integers we can also conclude that 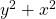 is even. Thus
is even. Thus 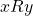 and
and 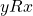 so
so 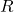 is symmetric.
is symmetric. - Transitive: For
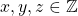 , if
, if 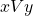 then
then 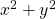 is even and if
is even and if 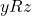 then
then 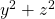 is even. We can also find that since
is even. We can also find that since 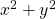 is even and
is even and 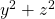 is even then the sum of the two is also even which gives us:
is even then the sum of the two is also even which gives us:
![]()
If we subtract the even value ![]()
![]()
An even minus an even is still even thus we can draw the conclusion that ![]() is even so
is even so ![]() , thus
, thus ![]() is transitive.
is transitive.
Since ![]() is reflexive, symmetric, and transitive then by definition of equivalence relations
is reflexive, symmetric, and transitive then by definition of equivalence relations ![]() is an equivalence relation.
is an equivalence relation.
This concludes our section on relations. In the next section we will continue discussing relation use but as it applies to functions and the classification of functions.
