16 Cardinality
We have mentioned in a previous section, the concept of infinite sets, and one might think that this means that the size is also infinite but that is where cardinality comes in. Cardinality is what we refer to when trying to define the size of an infinite set. we can also use cardinality to count the size of a finite set as well. When we consider the size of a set we aren’t thinking of big or little, we consider size by the count of how many elements are in the set. The elements are defined by the set, this means they can be natural, rational, integers, or real numbers.
Some might think “why does cardinality of an infinite or finite set matter?” what mathematicians say to this is cardinality allows us to compare sets and define relations between sets. To give a real world example cardinality is extremely important to the data modeling used in businesses, and without knowing how to determine cardinality we would be unable to create data models in the real world and for that matter be able to analyze any data brought in.
Lets now consider the cardinality for finite and infinite sets in greater detail by addressing them individually.
14.1 Finite Sets
We already know that cardinality means the size of a set and if a set is finite then the size of the set is just the number of elements in the set which can, tediously, be counted by hand. We can denote the cardinality of a set by ![]() for some
for some ![]() , given set
, given set ![]() . For example if
. For example if ![]() then we can say
then we can say ![]() . The other option is if a set
. The other option is if a set ![]() is empty then cardinality will be 0 because there are no elements in
is empty then cardinality will be 0 because there are no elements in ![]() . Instead of a formal definition for cardinality we will introduce the properties of a finite set in terms of cardinality [23].
. Instead of a formal definition for cardinality we will introduce the properties of a finite set in terms of cardinality [23].
Theorem: Fundamental Properties of Finite Sets
Suppose A and B are finite sets.
- Every subset of set
 is finite, and has cardinality less than or equal to the cardinality of
is finite, and has cardinality less than or equal to the cardinality of  .
. 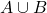 is finite, and the cardinality of
is finite, and the cardinality of 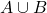 is equal to the cardinality of
is equal to the cardinality of 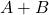 minus the cardinality of
minus the cardinality of  .
.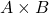 is finite, and the cardinality of
is finite, and the cardinality of 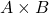 is equal to the cardinality of
is equal to the cardinality of  multiplied by the cardinality of
multiplied by the cardinality of 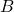 .
.
Now recall when we discussed functions and the concepts of one-to-one and onto. There are times where ![]() with
with ![]() and
and ![]() the cardinality of the set of
the cardinality of the set of ![]() is
is ![]() [25]. Now this works very well for finite sets that are a one-to-one correspondence but from our previous section on functions we know not all functions are one-to-one or onto. With this in mind we introduce the pigeon hole principle [25].
[25]. Now this works very well for finite sets that are a one-to-one correspondence but from our previous section on functions we know not all functions are one-to-one or onto. With this in mind we introduce the pigeon hole principle [25].
Theorem: The Pigeonhole Principle
Let ![]() and
and ![]() be finite sets. if
be finite sets. if ![]() and
and ![]() , then there exists distinct elements
, then there exists distinct elements ![]() such that
such that ![]() .
.
This means for two elements in ![]() there is only one element in
there is only one element in ![]() . This just goes to show that sets do not need to be equal under a function. We can consider set equality by introducing the definition of equality [30].
. This just goes to show that sets do not need to be equal under a function. We can consider set equality by introducing the definition of equality [30].
Definition. Set Equality
Two sets are equal if, and only if, for all ![]() then
then ![]() .
.
Given this definition we can prove that two sets are equal through the use of cardinality. Lets consider the proof below.
Example:
True or False: Let ![]() and
and ![]() be finite sets with
be finite sets with ![]() , if
, if ![]() then
then ![]() .
.
True, if ![]() then
then ![]() and
and ![]() have the same number of elements. Since we are given that
have the same number of elements. Since we are given that ![]() and we know
and we know ![]() then
then ![]() is not a proper subset of
is not a proper subset of ![]() and thus
and thus ![]() .
.
Here we can see that we do not need to prove both ![]() and
and ![]() in order to prove
in order to prove ![]() , we can use cardinality instead. Now it’s important to note that this is only for finite sets since an infinite set can be a subset of another with the same cardinality but that does not mean they are equal. We will look at some examples of this in the next section, Infinite Sets.
, we can use cardinality instead. Now it’s important to note that this is only for finite sets since an infinite set can be a subset of another with the same cardinality but that does not mean they are equal. We will look at some examples of this in the next section, Infinite Sets.
14.2 Infinite Sets
We have already explored what cardinality is and how we can apply it to finite sets so lets begin the topic of cardinality for infinite sets by first giving the definition [30].
Definition.
Let ![]() and
and ![]() be infinite sets. We say that
be infinite sets. We say that ![]() if there exists an onto function
if there exists an onto function ![]() .
.
Using cardinality we can categorize infinite sets as either countable of uncountable sets. If we think about our number families as sets we have sets such as real numbers ![]() , rational numbers
, rational numbers ![]() , integers
, integers ![]() , natural numbers
, natural numbers ![]() . We define an infinite set
. We define an infinite set ![]() to be countable if
to be countable if ![]() which means that set
which means that set ![]() has a one-to-one correspondance with set
has a one-to-one correspondance with set ![]() , counter to this, if a set
, counter to this, if a set ![]() has a cardinality such that
has a cardinality such that ![]() then we say that
then we say that ![]() is uncountable. Now when a list can be established for the objects to be counted in a set we say the set is enumerable. We have an established definition for both enumerable finite sets and enumerable infinite sets below [30].
is uncountable. Now when a list can be established for the objects to be counted in a set we say the set is enumerable. We have an established definition for both enumerable finite sets and enumerable infinite sets below [30].
Definition.
A set ![]() is finite if and only if the elements of
is finite if and only if the elements of ![]() can be enumerated in a terminating list as
can be enumerated in a terminating list as ![]() .
.
Thus we can say that all finite sets are enumerable [30].
Definition.
A set ![]() is countably infinite if and only if the elements of
is countably infinite if and only if the elements of ![]() can be enumerated in an endless list as
can be enumerated in an endless list as ![]() .
.
Now not every infinitely countable set is enumerable, if a set ![]() has cardinality such that
has cardinality such that ![]() then
then ![]() is what we call denumerable. This may seem a bit all over the place with countability and enumerable and denumerable sets. Lets examine some true or false logic statements to get some clarity.
is what we call denumerable. This may seem a bit all over the place with countability and enumerable and denumerable sets. Lets examine some true or false logic statements to get some clarity.
- If a set
 is denumerable, then
is denumerable, then  is countable. This is true because a denumerable set must be both countable and infinite [20].
is countable. This is true because a denumerable set must be both countable and infinite [20]. - If a set
 is not denumerable, then
is not denumerable, then  is uncountable. This is false because
is uncountable. This is false because  can still be countable even if it is not denumerable. The definition for countable sets states that a set can either be finite or denumerable [20].
can still be countable even if it is not denumerable. The definition for countable sets states that a set can either be finite or denumerable [20]. - If a set
 is enumerable, then
is enumerable, then  is countable. This is true because a countable set must either be enurmerable or denumerable and all enumerable sets must then be countable.
is countable. This is true because a countable set must either be enurmerable or denumerable and all enumerable sets must then be countable.
Let’s now consider one example before we continue on.
Example:
Prove that the set ![]() is denumerable [20].
is denumerable [20].
Proof: Assume that set ![]() then there is a function
then there is a function ![]() where
where ![]() . Let
. Let ![]() then
then ![]() , now if we subtract
, now if we subtract ![]() from both sides and we find
from both sides and we find ![]() thus we can say
thus we can say ![]() is one-to-one. Next, let there be
is one-to-one. Next, let there be ![]() such that for
such that for ![]() it follows that
it follows that ![]() thus we can conclude that
thus we can conclude that ![]() is onto so
is onto so ![]() is a bijection or one-to-one correspondence which means
is a bijection or one-to-one correspondence which means ![]() is denumerable and
is denumerable and ![]() .
.
It took some amazing brain power to be able to establish these ideas for sizing infinite sets, we can credit a lot of what we have seen in this section to Georg Cantor who established the idea of uncountable infinites, began to establish the idea that infinite sets can be different sizes and thus qualify some to be considered countable and others as uncountable [33]. Cantor also coined the “Cantor’s set” seen below.
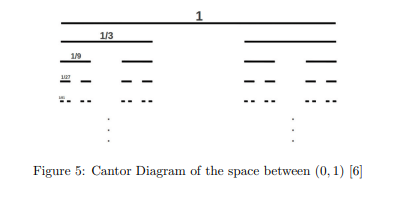
This illustration shows the breakdown of the infinite set within the interval from 0 to 1. This discovery led to Cantor’s Diagonal Argument over the countable nature of the interval ![]() . The argument proves that the set of all real numbers on the interval
. The argument proves that the set of all real numbers on the interval ![]() is uncountable. We can see the argument supporting Cantor’s conclusion here.
is uncountable. We can see the argument supporting Cantor’s conclusion here.
Example:
Prove that the set ![]() is uncountable [20].
is uncountable [20].
Proof: Let the set ![]() and assume
and assume ![]() is countable such that
is countable such that ![]() has a one-to-one correspondence. We are then able to produce the following sequences.
has a one-to-one correspondence. We are then able to produce the following sequences.

We can observe that ![]() symbolizes a decimal between 0 and 9 that form a real number with a decimal expansion
symbolizes a decimal between 0 and 9 that form a real number with a decimal expansion ![]() . The digits are determined by the following rule.
. The digits are determined by the following rule.
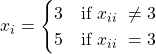
Each expansion is unique and this means that the real number ![]() cannot be equal to any decimal expansion. This is because the expansion of
cannot be equal to any decimal expansion. This is because the expansion of ![]() is not the same as the
is not the same as the ![]() th term in the decimal expansion
th term in the decimal expansion ![]() for
for ![]() . Therefore there is a real number
. Therefore there is a real number ![]() that is not included, this contradicts the assumption that
that is not included, this contradicts the assumption that ![]() has a one-to-one correspondence. If
has a one-to-one correspondence. If ![]() had a one to one correspondence then every element in
had a one to one correspondence then every element in ![]() would map to an
would map to an ![]() . Since this is not true then not every element between
. Since this is not true then not every element between ![]() and
and ![]() can be accounted for and thus we must conclude that the set
can be accounted for and thus we must conclude that the set ![]() is uncountable.
is uncountable.
