22 Limits and Continuity
We covered much about limits and continuity in calculus but we need to apply it to analysis. Lets first give the formal definition for functional limits under analysis.
Definition. Functional Limits
Let ![]() , and let
, and let ![]() be a limit point of the domain
be a limit point of the domain ![]() . The limit,
. The limit, ![]() if, for all
if, for all ![]() , there exists a
, there exists a ![]() such that whenever
such that whenever ![]() for
for ![]() it follows that
it follows that ![]() .
.
We have already been familiarized with ![]() and we can say that
and we can say that ![]() carries the same meaning for neighborhood but we utilize both because the open neighborhood for
carries the same meaning for neighborhood but we utilize both because the open neighborhood for ![]() will not always be the same as the open neighborhood for
will not always be the same as the open neighborhood for ![]() . Lets look at an example of how we can use the value for
. Lets look at an example of how we can use the value for ![]() to determine the largest value for
to determine the largest value for ![]() which will thus return the largest open neighborhood that can possibly satisfy the limit.
which will thus return the largest open neighborhood that can possibly satisfy the limit.
Example:
![]() , where
, where ![]() . Find the largest
. Find the largest ![]() which satisfies the limit [3].
which satisfies the limit [3].
Proof: Let ![]() . Since
. Since ![]() then
then ![]() . We first need to simplify this inequality. Firstly we can rewrite
. We first need to simplify this inequality. Firstly we can rewrite ![]() as follows:
as follows:
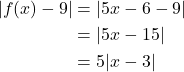
Thus, ![]() and if we divide both sides by
and if we divide both sides by ![]() we get
we get ![]() . Now, let
. Now, let ![]() then
then ![]() such that
such that ![]() is the same as
is the same as ![]() which simplifies to
which simplifies to ![]() and since
and since ![]() then
then ![]() . Thus for
. Thus for ![]() with
with ![]() , we find the largest
, we find the largest ![]() .
.
There is a really valuable visual explanation, given below, of the epsilon and delta neighborhoods and what we are focusing on within a function when we analyze these limits.
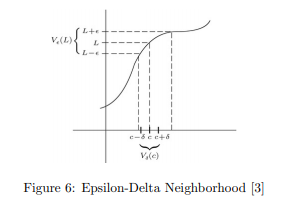
We can see form this illustration, how ![]() and
and ![]() neighborhoods associate with functions and point
neighborhoods associate with functions and point ![]() . Using neighborhoods to prove limits is like narrowing down the range and domain for which a limit point may be. Given a better understanding of the relationship between neighborhoods let us look at one more example where we have to determine an appropriate
. Using neighborhoods to prove limits is like narrowing down the range and domain for which a limit point may be. Given a better understanding of the relationship between neighborhoods let us look at one more example where we have to determine an appropriate ![]() and
and ![]() .
.
Example:
Given ![]() , prove the limit.
, prove the limit.
Proof: Let ![]() , Let
, Let ![]() then to find
then to find ![]() such that
such that ![]() we need
we need ![]() . We first simplify
. We first simplify ![]()
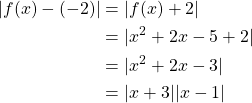
Here we can see that ![]() can be easily bounded by
can be easily bounded by ![]() as
as ![]() but
but ![]() will not be. If
will not be. If ![]() then
then ![]() and if we remove
and if we remove ![]() from
from ![]() by way of adding
by way of adding ![]() we get
we get ![]() so
so ![]() if
if ![]() . Let us considered that
. Let us considered that ![]() then, since
then, since ![]() we have
we have ![]() . Thus
. Thus ![]() and if we divide both sides by
and if we divide both sides by ![]() we find
we find ![]() . Now let
. Now let ![]() , if
, if ![]() then
then ![]() which we simplify to
which we simplify to ![]() . Thus we conclude that
. Thus we conclude that ![]() .
.
Now we can expand on what we have already proven by introducing the definition of continuity as it pertains to analysis.
Definition. Continuity
A function ![]() is continuous at a point
is continuous at a point ![]() if, for all
if, for all ![]() , there exists a
, there exists a ![]() such that whenever
such that whenever ![]() for
for ![]() it follows that
it follows that ![]() [3].
[3].
This definition is very similar to our definition for functional limits with one major difference. Instead of finding neighborhoods that satisfy the limit of the function we are now looking at finding the neighborhood that satisfies the point ![]() for
for ![]() .
.
Example:
Prove that ![]() is continuous on
is continuous on ![]() [3].
[3].
Proof: Let ![]() then there is
then there is ![]() for all
for all ![]() .
.
Part 1) If ![]() then
then ![]() . We rewrite
. We rewrite ![]() by the following:
by the following:
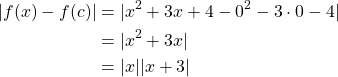
Thus ![]() .
. ![]() can easily be bounded by
can easily be bounded by ![]() as
as ![]() because
because ![]() where
where ![]() . If
. If ![]() then
then ![]() so
so ![]() if
if ![]() . Let
. Let ![]() then since
then since ![]() and
and ![]() we can divide both sides by
we can divide both sides by ![]() to find
to find ![]() . Now let
. Now let ![]() , if
, if ![]() then
then ![]() which simplifies to
which simplifies to ![]() .
.
Part 2) If ![]() then
then ![]() can be simplified by
can be simplified by
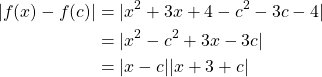
Where ![]() .
. ![]() can easily be bounded by
can easily be bounded by ![]() . If
. If ![]() then
then ![]() can easily become
can easily become ![]() by adding
by adding ![]() and then, by removing
and then, by removing ![]() from the center and adding it to either side we find
from the center and adding it to either side we find ![]() so
so ![]() if
if ![]() . Now
. Now ![]() and
and ![]() then we can simplify this inequality by dividing both sides by
then we can simplify this inequality by dividing both sides by ![]() to get
to get ![]() . Let
. Let ![]() , if
, if ![]() then
then ![]() which simplifies to
which simplifies to ![]() .
.
Thus we can conclude that ![]() is continuous on
is continuous on ![]()
Building on our understanding of continuity we introduce the following theorem [3].
Theorem: The Intermediate Value Theorem
Let ![]() be continuous. If
be continuous. If ![]() is a real number satisfying
is a real number satisfying ![]() of
of ![]() , then there exists a point
, then there exists a point ![]() where
where ![]() .
.
Example:
Let ![]() be continuous with
be continuous with ![]() . Show that there must exist
. Show that there must exist ![]() satisfying
satisfying ![]() and
and ![]() [3].
[3].
Proof: Let ![]() and let
and let ![]() be a continuous function
be a continuous function ![]() such that
such that ![]() which leads us to conclude
which leads us to conclude ![]() such that
such that ![]() and since
and since ![]() then
then ![]() such that
such that ![]() . We can observe from these inequalities that at some point on the interval
. We can observe from these inequalities that at some point on the interval ![]() because the value of
because the value of ![]() changes from greater than 0 to less than 0. Consider a point
changes from greater than 0 to less than 0. Consider a point ![]() such that
such that ![]() then
then ![]() . Thus there exists an
. Thus there exists an ![]() such that
such that ![]() and
and ![]() .
.
Expanding even further on continuity we look, now, to uniform continuity which is a stricter class of continuity.
19.1 Uniform Continuity
Previously mentioned uniform continuity is a stricter class of continuity. What this means is that instead of proving continuity by points, uniform continuity simply utilizes the ![]() -neighborhood to prove continuity.
-neighborhood to prove continuity.
Definition. Uniform Continuity
The function ![]() is uniformly continuous on interval
is uniformly continuous on interval ![]() if for every
if for every ![]() , there exists a
, there exists a ![]() such that for
such that for ![]() for
for ![]() it follows that
it follows that ![]() [3].
[3].
It goes without need for explanation that if ![]() is uniformly continuous then
is uniformly continuous then ![]() is continuous on the given interval.
is continuous on the given interval.
Example:
Prove that ![]() is uniformly continuous on
is uniformly continuous on ![]() .
.
Proof:Let ![]() then by the definition of uniform continuity
then by the definition of uniform continuity
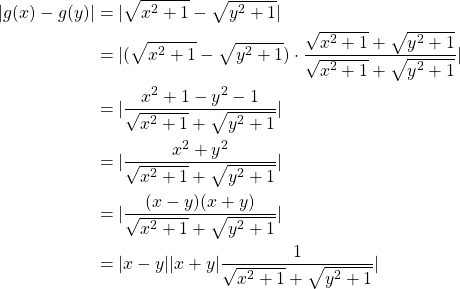
Now we let ![]() such that
such that ![]() then we can conclude that
then we can conclude that
![]()
if ![]() and
and ![]() . Let
. Let ![]() such that
such that
![]()
Let ![]() then, by dividing both sides by 2, we get
then, by dividing both sides by 2, we get ![]() such that
such that
![]()
Can be rewritten as
![]()
Which is equivalent to
![]()
Thus if ![]() the
the ![]() . Thus we con conclude that
. Thus we con conclude that ![]() is uniformly continuous on
is uniformly continuous on ![]() .
.
