27 Rings of Polynomials
Definition. Polynomial Rings
Let ![]() be a ring. A polynomial
be a ring. A polynomial ![]() with coefficient
with coefficient ![]() in
in ![]() is an infinite formal sum given as
is an infinite formal sum given as
![]()
where ![]() and
and ![]() for all but a finite number of values of
for all but a finite number of values of ![]() [12].
[12].
Here we have ![]() as a coefficient of
as a coefficient of ![]() . We call a degree of
. We call a degree of ![]() the largest value for
the largest value for ![]() such that
such that ![]() . Just like rings have two binary operations such that terms in a ring can be added together of multiplied the same is true for rings of polynomials.
. Just like rings have two binary operations such that terms in a ring can be added together of multiplied the same is true for rings of polynomials.
Example:
Find the sum and the product of the given polynomials in the given polynomial ring. ![]() ,
, ![]() in
in ![]() [12].
[12].
Let us compute the sum first
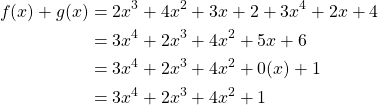
Next, let us compute the product of ![]()
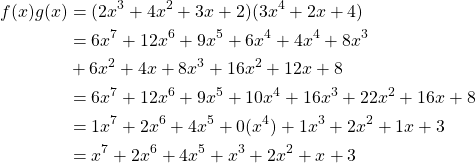
Thus we can conclude that the sum ![]() and the product
and the product ![]()
In this example we used a familiar technique for simplification as used in finding the solutions to an integral domain problem. This technique comes into play prominently in Abstract Algebra and we will cover it in depth in our section on Number Theory. For now we look at some basic commonalities between what we know of ring properties and what see are properties of ring polynomials. We can add or multiply polynomials and we will see that there are different families for which these rings may fall, just as we saw in the diagram in the previous section.
Theorem:
The set ![]() of all polynomials in an indeterminate
of all polynomials in an indeterminate ![]() with the coefficients in a ring
with the coefficients in a ring ![]() is a ring under polynomial addition and multiplication. If
is a ring under polynomial addition and multiplication. If ![]() is commutative, then so is
is commutative, then so is ![]() , and if
, and if ![]() has unity
has unity ![]() , then 1 is also unity for
, then 1 is also unity for ![]() .
.
We see here that even for Polynomial rings we can still classify them as commutative if the ring ![]() of the polynomial ring
of the polynomial ring ![]() is commutative. Recall the diagram given in the previous section, we saw that within a portion of commutative rings we found integral domains and within the family of integral domains we found fields. It would be rational to expect that there is a family of commutative rings of polynomials that can be classified as fields as well [12].
is commutative. Recall the diagram given in the previous section, we saw that within a portion of commutative rings we found integral domains and within the family of integral domains we found fields. It would be rational to expect that there is a family of commutative rings of polynomials that can be classified as fields as well [12].
Definition. Fields
Let ![]() be a field, then
be a field, then ![]() is an integral domain and as such
is an integral domain and as such ![]() is the field of quotients for
is the field of quotients for ![]() . Thus any element in
. Thus any element in ![]() can be represented as a quotient
can be represented as a quotient ![]() of two polynomials in
of two polynomials in ![]() where
where ![]() .
.
We can relate this definition to polynomial functions by stating that if ![]() is an integral domain with a field of quotients
is an integral domain with a field of quotients ![]() then the field of quotients is a field of rational functions in
then the field of quotients is a field of rational functions in ![]() indeterminates over
indeterminates over ![]() [12].
[12].
Now that we have an established understanding of fields as they pertain to polynomials we can look at properties of polynomials [12].
Theorem: Evaluation Homomorphism
Let ![]() and
and ![]() be fields, with
be fields, with ![]() . Suppose that
. Suppose that ![]() factors in
factors in ![]() , so that
, so that ![]() for
for ![]() and let
and let ![]() . For the evaluation homomorphism
. For the evaluation homomorphism ![]() , there is
, there is ![]() . Thus if
. Thus if ![]() , then
, then ![]() if and only if either
if and only if either ![]() or
or ![]() .
.
From this we can draw out that the purpose of homomorphisms is much the same as it always has been but we evaluate now by using the value of ![]() and although we may be solving for a zero of
and although we may be solving for a zero of ![]() we may run into polynomials that have a remainder and this simply means that whatever the value of the remainder is, we claim as our solution. We can see this in the following example.
we may run into polynomials that have a remainder and this simply means that whatever the value of the remainder is, we claim as our solution. We can see this in the following example.
Example:
Let ![]() . Compute for
. Compute for ![]() [12].
[12].
Given our understanding of the evaluation homomorphisms for field theory consider that ![]() then we have the following.
then we have the following.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \phi_{3}[(x^{4}+2x)(x^{3}-3x^{2}+3)]&=(3^{4}+2(3))(3^{3}-3(3)^{2}+3)\\ &=(81+6)(27-27+3)\\ &=87\cdot 3\\ &=261 \end{split} \end{equation*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a0fcc1a9b165d85fb4f1ddaa43dc1b7f_l3.png)
Since ![]() for
for ![]() , we can simplify 261 if we divide 261 by 7 we get a remainder of 2 thus we can conclude that
, we can simplify 261 if we divide 261 by 7 we get a remainder of 2 thus we can conclude that ![]() .
.
Just as we discussed in the definition for the Evaluation Homomorphism for field theory, we are given a polynomial with a distinguished ![]() which we used to solve the function to a quantifiable value 261. We then used the field
which we used to solve the function to a quantifiable value 261. We then used the field ![]() which we knew meant that we have to simplify 261 by factors of 7 which would either result in 0 or would result in the remainder between 261 and
which we knew meant that we have to simplify 261 by factors of 7 which would either result in 0 or would result in the remainder between 261 and ![]() where
where ![]() is the number of times 7 is multiplied to produce the value closest but smaller than 261.
is the number of times 7 is multiplied to produce the value closest but smaller than 261.
We can continue our understanding of polynomials over fields by discussing the factorization of polynomials. It might seem backwards at first but the best way to find the factor of ![]() is by division, thus it is only natural for there to be a theorem for the division of
is by division, thus it is only natural for there to be a theorem for the division of ![]() [12].
[12].
Theorem: Division Algorithm
Let ![]() and
and ![]() be two elements of
be two elements of ![]() , with
, with ![]() and
and ![]() both nonzero elements of
both nonzero elements of ![]() and
and ![]() . Then there are unique polynomials
. Then there are unique polynomials ![]() and
and ![]() in
in ![]() such that
such that ![]() , where either
, where either ![]() of the degree of
of the degree of ![]() is less than the degree
is less than the degree ![]() of
of ![]() .
.
Example:
Find ![]() and
and ![]() as described by the division algorithm
as described by the division algorithm ![]() and
and ![]() in
in ![]() so that
so that ![]() with
with ![]() or of degree less than the degree of
or of degree less than the degree of ![]() .[12]
.[12]
Consider the long division
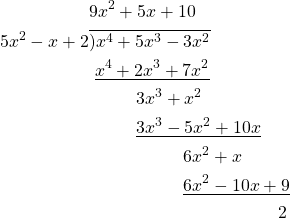
Thus we have found ![]() and
and ![]() .
.
This example is a wonderfully simple way of understanding the relationship between ![]() and
and ![]() . At first this long division might look wrong but we need to keep in mind that we have
. At first this long division might look wrong but we need to keep in mind that we have ![]() so we can alter values in terms of multiples of 11 with remainder, again this will be explained more in depth in our section on number theory.
so we can alter values in terms of multiples of 11 with remainder, again this will be explained more in depth in our section on number theory.
We continue our discussion on polynomials by introducing another way to look at our long division problem [12].
Theorem: Factor Theorem
An element ![]() is a zero of
is a zero of ![]() if and only if
if and only if ![]() is a factor of
is a factor of ![]() in
in ![]() .
.
We understand this theorem easily because we know that ![]() can only be a zero if it is a factor of
can only be a zero if it is a factor of ![]() otherwise there is a remainder. This can be seen when we look at the formula for
otherwise there is a remainder. This can be seen when we look at the formula for ![]() if
if ![]() is a zero then we can simplify this formula to
is a zero then we can simplify this formula to ![]() . There is a formal proof for this theorem but we will use the brief explanation, allowing us to focus our attention on the next vital definition in Rings of Polynomials.
. There is a formal proof for this theorem but we will use the brief explanation, allowing us to focus our attention on the next vital definition in Rings of Polynomials.
Definition.
A non-constant polynomial ![]() is irreducible over
is irreducible over ![]() or is irreducible polynomial in
or is irreducible polynomial in ![]() if
if ![]() cannot be expressed as a product
cannot be expressed as a product ![]() of two polynomials
of two polynomials ![]() and
and ![]() in
in ![]() both of lower degree than the degree of
both of lower degree than the degree of ![]() . If
. If ![]() is a non-constant polynomial that is not irreducible over
is a non-constant polynomial that is not irreducible over ![]() , then
, then ![]() is reducible over
is reducible over ![]() .
.
Example:
Demonstrate that ![]() is irreducible over
is irreducible over ![]() [12].
[12].
Firstly, we see that ![]() is of degree 4. The only possibility for
is of degree 4. The only possibility for ![]() to be irreducible in
to be irreducible in ![]() is if, either there are no roots in
is if, either there are no roots in ![]() or
or ![]() can not be factored in a polynomial of degree 2. Since
can not be factored in a polynomial of degree 2. Since ![]() then we can say if
then we can say if ![]() has a zero in
has a zero in ![]() then
then ![]() also has a zero in
also has a zero in ![]() that must divide 1. This leaves us with only two options
that must divide 1. This leaves us with only two options ![]() or
or ![]() .
.
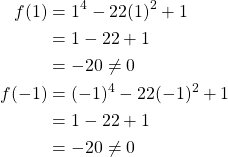
Since there are no zeros ![]() has no linear factors over
has no linear factors over ![]() . Now let us address
. Now let us address ![]() where
where ![]() . Let
. Let
![]()
we can expand this equivalency to result in
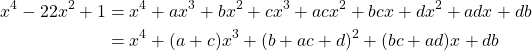
If we evaluate the newly simplified form we see that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Firstly, if
. Firstly, if ![]() then
then ![]() or
or ![]() . Let
. Let ![]() , then
, then ![]() and if we subtract
and if we subtract ![]() from both sides we get
from both sides we get ![]() . Since
. Since ![]() then
then ![]() and as such
and as such ![]() which is impossible for
which is impossible for ![]() . Now let
. Now let ![]() then
then ![]() . If we subtract
. If we subtract ![]() from both sides we get
from both sides we get ![]() and since
and since ![]() then
then ![]() this is also not possible for
this is also not possible for ![]() . Therefore we can conclude that
. Therefore we can conclude that ![]() has no quadratic factors over
has no quadratic factors over ![]() nor
nor ![]() and thus we say
and thus we say ![]() is irreducible over both.
is irreducible over both.
What we can derive from this example is that if the polynomial ![]() is irreducible then there can be no two polynomials, which must be of a lower degree, whose product is
is irreducible then there can be no two polynomials, which must be of a lower degree, whose product is ![]() . When we say of lower degree we say in the previous example that
. When we say of lower degree we say in the previous example that ![]() was given a degree of 4, this is because the leading
was given a degree of 4, this is because the leading ![]() variable had an exponent of 4. So the two polynomials
variable had an exponent of 4. So the two polynomials ![]() and
and ![]() that might produce
that might produce ![]() must have a leading variable with an exponent
must have a leading variable with an exponent ![]() . In the example we saw that both polynomials had an exponent equal to 2.
. In the example we saw that both polynomials had an exponent equal to 2.
This last theorem is another way we can classify a polynomials under a ring. All of these classifications help us better understand functions that arise and what properties they have based on their classification. For example, if you were to be given an ![]() and told nothing other than the fact it was reducible over
and told nothing other than the fact it was reducible over ![]() you would instantly know that
you would instantly know that ![]() was a polynomials in a field that could be factored into two separate polynomials.
was a polynomials in a field that could be factored into two separate polynomials.
