Congruence

Maggie Schildt

31 Congruence

We have seen congruence before just not with a greater understanding of what it means as we will cover in this section. In our previous discussions on rings we noted a way of simplifying a value by putting it in terms of $n$ for $\mathbb{Z}_{n}$ this is congruence. The format for congruence is $a=b \left( \mod m\right)$ , this translates to $a-b$ is divisible by $m$ .

Definition. Congruence

Let $m$ be a positive integer also called modulus. We say two integers $a$ and $b$ are congruent mod $m$ , written as $a=b \left( \mod m\right)$ , if $n|b-a$ .

Some basic examples are as follows:

Example:

Given 47 find the congruence with respect to modulus 5. If we divided 47 by 5 we would get 9 with a remainder of 2 thus we can write the congruence as $47=2 \left( \mod5\right)$ or $47=-3 \left( \mod 5\right)$ .

This is the basic congruence problem one might encounter in number theory, and just like Modern Algebra, Number theory too studies the properties of it’s structures. With the basic understanding of congruence we introduce the following properties.

Theorem:

Let $m$ be a positive integer.

1) For all $a\in \mathbb{Z}$ it follows that $a=a \left( \mod m\right)$ .

2) For all $a,b\in \mathbb{Z}$ if $a=b \left( \mod m\right)$ , then $b=a \left( \mod m\right)$ .

3) For all $a,b,c\in \mathbb{Z}$ , if $a=b \left( \mod m\right)$ and $b=c \left( \mod m\right)$ , then $a=c \left( \mod m\right)$ .

These properties should look very familiar as they are essentially the reflexive, symmetric, and transitive properties of a congruence. The same rules apply as they always have where a congruence need not satisfy every property but if they do then we call this an equivalence relation. We can see here just how many similarities there are between different studies of abstract mathematics; all the axioms and properties that transcend a mathematical division. Congruences even act the same way common numbers do, under arithmetic, in the sense we can add and subtract congruences and even multiply them. Below are the axioms for congruence under addition and multiplication [13].

Theorem:

Let $m\in \mathbb{Z}$ be positive, then for all $a,b,c\in \mathbb{Z}$ the following axioms apply:

1) Associativity of Addition: $(a+b)+c=a+(b+c) (\mod m)$

2) Commutativity of Addition: $a+b=b+a (\mod m)$

3) Associativity of Multiplication: $(a\cdot b)\cdot c = a \cdot (a \cdot b) (\mod m)$

4) Commutativity of Multiplication: $a \cdot b = b \cdot a (\mod m)$

5) Additive Inverse: $a+(-a) = 0 (\mod m)$

6) Additive Identity: $a+0=a (\mod m)$

7) Multiplicative Identity: $a \cdot 1 = a (\mod m)$

8) Distribution over Addition: $a\cdot (b+c) = ab + ac(\mod m)$

When we look at all these axioms they are already so familiar and this is because number theory is the study of numbers so naturally if we look at set theory or the topology of $\mathbb{R}$ associative and commutative properties, although they may be slightly adjusted for application on the structure of a congruence or the structure of a set or elements in a set, the same theorem applies. It is a beautiful way to see how interconnected different studies of mathematics are.

We already have an established understanding of the structure of primes which is required for comprehending the next theorem vital to the properties of congruence.

Theorem: Little Theorem of Fermat

If $a\in \mathbb{Z}$ and $p$ is a prime not dividing $a$ , then $p$ divides $a^{p-1}-1$ , that is, $a^{p-1}=1 (\mod p)$ for $a\neq 0 (mod p)$ .

We can test this theorem in the following example.

Example:

Using Fermat’s Theorem, find the remainder of $3^{47}$ when it is divided by $23$ [12].

$\begin{equation*} \begin{split} 3^{47}&=(3^{44})(3^{3})\\ &=(3^{22})^{2}(3^{3})\\ &=(1^{2})(3^{3})\\ &=3^{3}\\ &=27\\ &=4 (\mod 23) \end{split} \end{equation*}$

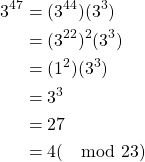
Thus we find the remainder to be 4.

There is not much to explain here as Fermat’s theorem is method by which we calculate the remainder of a large values when divided by smaller values, a task which by hand would be tedious by hand. Much of what we see in theoretical mathematics are theorems that we can utilize to justify or simplify the process of finding a solution to mathematical calculations that otherwise might seem near impossible to solve. So many of the theorems that provide properties and structure to mathematical concepts were developed by observing patterns and were then proven arbitrarily so that we might use them today to streamline calculations and make way for future discoveries far beyond what was has been established thus far.

The last congruence we will introduce, before moving on to the Euclidean Algorithm, is linear congruence [12].

Definition. Linear Congruence

Let $m$ be a positive integer and let $a\in \mathbb{Z}_{m}$ be relatively prime to $m$ . For each $b\in \mathbb{Z}_{m}$ , the equation $ax=b (\mod m)$ has a unique solution.

In order to be able to prove there is a solution to a linear congruence problem we need to know the Eucidean algorithm for the greatest common divisor and the theorems we will use as axioms to determine if there is in fact even a potential for a solution given a linear congruence.

31 Congruence

License

Share This Book