37 Differential Equations
Referring back to calculus again, recall implicit differentiation which involved attempting to differentiate an equation that contained more than one variable. Recall that we denote the first derivative for a differential equations as ![]() . Where we are taking the derivative of
. Where we are taking the derivative of ![]() with respect to time
with respect to time ![]() . We can apply this to any variable though, the main focus is that
. We can apply this to any variable though, the main focus is that ![]() illustrates the change in
illustrates the change in ![]() over the change in
over the change in ![]() . To calculate this we need to find the limit of
. To calculate this we need to find the limit of ![]() as
as ![]() approaches
approaches ![]() . Since we cannot directly substitute
. Since we cannot directly substitute ![]() for
for ![]() we need to calculate the values for the change in
we need to calculate the values for the change in ![]() close to
close to ![]() . This will allow us to approximate the limit of
. This will allow us to approximate the limit of ![]() [16]. We find the formula by first acknowledging that
[16]. We find the formula by first acknowledging that ![]() where
where
![]()
We define this formula as Euler’s method. Here we see that the formula is to calculate the value of the current step using the previous value, similar to the idea in the Newton-Raphson and Secant methods. We can use a different array of variables, as well, to fit the formula as we see done in our next example.
Example:
Consider the equation ![]() . Given
. Given ![]() and
and ![]() , compute
, compute ![]() and
and ![]() using the Euler’s method. Compare to the exact solution
using the Euler’s method. Compare to the exact solution ![]() [15].
[15].
First we need to write out the Euler’s formula as it fits for our problem with the information we have been provided thus far.
![]()
We know that ![]() thus we have the following calculations:
thus we have the following calculations:
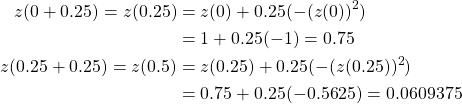
Now that we have found the values for ![]() and
and ![]() we need to compare them to the exact solution
we need to compare them to the exact solution ![]() .
.
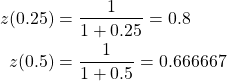
Now to compare our calculations we find the true error for each.
![]()
From this example we can see that although the approximations are close we will need several more iterations before we begin to see smaller and smaller errors which signify that the approximations are coming closer to the exact solutions.
There is a revised version of Euler’s method, called improved Euler’s method or Heun’s method.
31.1 Improved Euler’s Method
As mentioned previously, the improved Euler’s method is a revised verion of the original formula but with a two step process for every one calculation we performed for the original Euler’s method. We change the notation in order to better understand the iterations involved. Let ![]() be the previous known value and let
be the previous known value and let ![]() be the rough approximation for the current value used to approximate the the final value,
be the rough approximation for the current value used to approximate the the final value, ![]() . We define the two steps, using our same variables as for the Euler’s method, as follows.
. We define the two steps, using our same variables as for the Euler’s method, as follows.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} Step \ 1) \ & V^{*}_{n+1}=V_{n}+f(t_{n},V_{n}) \bigtriangleup t\\ Step \ 2) \ & V_{n+1}=V_{n}+\frac{\bigtriangleup t}{2} [f(t_{n},V_{n})+ f(t_{n+1}, V_{n+1})] \end{split} \end{equation*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5fbc08dc84fd6de79430362d0aa8a1cd_l3.png)
Using the previous example we used for Euler’s method lets us now apply the improved Euler’s method.
Example:
Consider the equation ![]() . Given
. Given ![]() and
and ![]() , compute
, compute ![]() and
and ![]() using the improved Euler’s method. Compare to the exact solution
using the improved Euler’s method. Compare to the exact solution ![]() [15].
[15].
We define our two steps for this problem as follows:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} Step \ 1) \ & z^{*}_{n+1}=z_{n}+0.25(-(z_{n})^{2})\\ Step \ 2) \ & z_{n+1}=z_{n}+\frac{0.25}{2}[(-(z_{n})^{2})+(-(z^{*}_{n+1})^{2})] \end{split} \end{equation*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bcba6f1d4604fcd2ad0017e1c6f2c8f1_l3.png)
Where ![]() , we can calculate
, we can calculate ![]() and
and ![]() beginning with
beginning with ![]() .
.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} z^{*}_{0+1}&=z_{0}+0.25(-(z_{0})^{2})=1+0.25(-(1)^{2})\\ &=1-0.25=0.75\\ z_{1}&=z_{0}+0.125[(-(z_{0})^{2})+(-(z^{*}_{1})^{2})]=1+0.125[(-(1)^{2})+(-(0.75)^{2})]\\ &=1+0.125(-0.1953125)=0.8046875 \end{split} \end{equation*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-59a091dd435d65c074a2e6e3477c3581_l3.png)
Next we calculate ![]() .
.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} z^{*}_{1+1}&=z_{1}+0.25(-(z_{1})^{2})=0.8046875+0.25(-(0.8046875)^{2})\\ &=0.8046875-0.161881=0.642807\\ z_{2}&=z_{1}+0.125[(-(z_{1})^{2})+(-(z^{*}_{2})^{2})]\\ &=0.8046875+0.125[(-(0.8046875)^{2})+(-(0.642807)^{2})\\ &=0.8046875+0.125(-1.060723)=0.672097 \end{split} \end{equation*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-15b6b6b88a55379637060696fe10d790_l3.png)
Now we calculate the true error between the exact values we already found in the previous example and the values, rounded to the 6th significant figure, found using the improved Euler’s method.
![]()
These are much lower true errors than what we found using the Euler’s method. Seeing the comparison between errors we can tell that the improved Euler’s method does, in fact, improve upon the approximations in comparison to the true values.
Now there is a third method that builds upon the improved Euler’s method to produce approximations with even better accuracy. In the next subsection we will learn how to utilize the fourth-order Runge-Kutta method for approximating differential equations.
31.2 Runge-Kutta Method
We can draw from the name that the fourth-order Runge-Kutta method requires 4 steps to calculate one approximation. The Runge-Kutta method is considered the more advanced as the more it has the greatest order. The Euler’s method was a first-order, with only one calculation to make an approximation. The improved Euler’s method was a second-order, as it required 2 sub-calculation to make an approximation. The Runge-Kutta method is a fourth-order because it requires 4 calculations to make an approximation. We define the formula for the fourth-order Runge-Kutta method as follows [16].
![]()
We define the calculations denoted by ![]() as the following:
as the following:
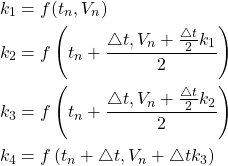
Using the same example we have used thus for in this section let us observe if the fourth-order Runge-Kutta method actually does improve upon Euler’s and improve Euler’s approximation.
Example:
Consider the equation ![]() . Given
. Given ![]() and
and ![]() , compute
, compute ![]() using the fourth-order Runge-Kutta method. Compare to the exact solution
using the fourth-order Runge-Kutta method. Compare to the exact solution ![]() [15].
[15].
We start with ![]() by calculating
by calculating ![]() .
.
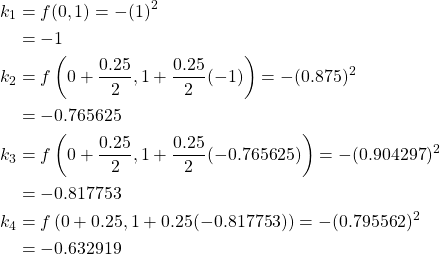
Now that we have found our values for ![]() we can input our known values into our formula and solve for
we can input our known values into our formula and solve for ![]() .
.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} z(0.25)&=z(0)+\frac{0.25}{6} [-1+2(-0.765625)+2(-0.817753)+(-0.632919)]\\ &=1+\frac{0.25}{6}(-4.799674)=0.800014 \end{split} \end{equation*}](https://iu.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-344eb36c29416979e3f744b106eb3937_l3.png)
We calculate the true error of this approximation using the exact value we found previously.
![]()
We don’t perform the calculation for ![]() in this example because just from calculating the true error of the fourth-order Runge-Kutta approximation for
in this example because just from calculating the true error of the fourth-order Runge-Kutta approximation for ![]() we see an extreme improvement. This new true error is even smaller than the one we found for our approximations using the improve Euler’s method. Just from comparing these examples we can see the progression of an approximation depending on the method you utilize to make the approximation.
we see an extreme improvement. This new true error is even smaller than the one we found for our approximations using the improve Euler’s method. Just from comparing these examples we can see the progression of an approximation depending on the method you utilize to make the approximation.
