2 Limits and Continuity
We begin this section with a basic description of what limits are. A formal definition of a limit is as follows [39]:
Definition. Limits
Let ![]() be a function defined on an open interval
be a function defined on an open interval ![]() containing
containing ![]() . If all values for
. If all values for ![]() approach a real number
approach a real number ![]() then the limit of
then the limit of ![]() , as
, as ![]() approaches
approaches ![]() is
is ![]() denoted by
denoted by
![]()
There are times in math when a quantifiable value cannot be calculated directly, this is where limits become very useful. There are many examples of when taking a limit is necessary, consider a function ![]() consisting of a fraction whose denominator
consisting of a fraction whose denominator ![]() is approaching zero. For this example we know it is impossible to simply substitute
is approaching zero. For this example we know it is impossible to simply substitute ![]() for the denominator thus we must take the limit as
for the denominator thus we must take the limit as ![]() approaches
approaches ![]() in order to find the value for the
in order to find the value for the ![]() . Another example may be calculating the value of a function
. Another example may be calculating the value of a function ![]() whose
whose ![]() is approaching
is approaching ![]() . Since it is impossible to calculate this by direct substitution we must take the limit of the function as
. Since it is impossible to calculate this by direct substitution we must take the limit of the function as ![]() approaches
approaches ![]() in order to find the value for
in order to find the value for ![]() . Limits allow us to find the value for a function
. Limits allow us to find the value for a function ![]() as
as ![]() approaches a finite or infinite value. With the concept of limits in mind we can briefly introduce continuity. When graphing points of a function on an
approaches a finite or infinite value. With the concept of limits in mind we can briefly introduce continuity. When graphing points of a function on an ![]() and
and ![]() plain we usually can draw a line between each graphed point. If this line holds throughout the entire plain we can say that the function is continuous because for every value
plain we usually can draw a line between each graphed point. If this line holds throughout the entire plain we can say that the function is continuous because for every value ![]() there is an
there is an ![]() . Now there are some functions that, when graphed, have open circles disconnecting the line through the plain. These types of functions are said to be discontinuous because for some value
. Now there are some functions that, when graphed, have open circles disconnecting the line through the plain. These types of functions are said to be discontinuous because for some value ![]() there is no
there is no ![]() . There are three conditions that a function must meet in order to be considered a continuous function, they are as follows [35]:
. There are three conditions that a function must meet in order to be considered a continuous function, they are as follows [35]:
Definition. Continuous Function
A function ![]() is said to be continuous at point
is said to be continuous at point ![]() if and only if the following axioms are satisfied:
if and only if the following axioms are satisfied: ![]() is defined,
is defined, ![]() exists, and
exists, and ![]() . A function is thus considered discontinuous at
. A function is thus considered discontinuous at ![]() if it fails one or more of these conditions.
if it fails one or more of these conditions.
2.1 Limit Laws
There are many different kinds of limits and each requires unique methods for solving. Below we will cover some of the basic laws for taking the limit of a function.
The Constant Rule
The first rule of limits is in regards to finding the limit of a constant. We begin with formal definition of the constant rule [35].
Definition.
Let ![]() be a constant value function such that for every value of
be a constant value function such that for every value of ![]() ,
, ![]() . Then the limit as
. Then the limit as ![]() approaches
approaches ![]() of
of ![]() , for
, for ![]() , is as follows:
, is as follows:
![]()
Example:
Let ![]() then as
then as ![]() approaches
approaches ![]() we have the following limit
we have the following limit
![]()
Direct Substitution
The next rule we will consider is direct substitution. If we let ![]() be our function with the limit as
be our function with the limit as ![]() approaches
approaches ![]() , for some
, for some ![]() we can substitute
we can substitute ![]() for
for ![]() with the following result [35]:
with the following result [35]:
![]()
We see in this basic example that since our ![]() finding the limit of
finding the limit of ![]() at
at ![]() is the same as letting
is the same as letting ![]() . Now let us consider when we manipulate the basic limit of
. Now let us consider when we manipulate the basic limit of ![]() .
.
The Constant Multiple Rule
Consider that ![]() is the arbitrary limit of
is the arbitrary limit of ![]() such that
such that ![]() . The constant multiple law states if
. The constant multiple law states if ![]() is a constant and
is a constant and ![]() is our function with the limit assigned above then the limit of
is our function with the limit assigned above then the limit of ![]() is as follows [35]:
is as follows [35]:
![]()
Example:
Consider ![]() , if
, if ![]() then
then
![]()
If we take the limit as ![]() approaches
approaches ![]() of
of ![]() we have
we have
![]()
thus by the constant multiple rule the limit as ![]() approaches
approaches ![]() for
for ![]() is
is
![]()
Power law for limits
Consider ![]() for the limit of function
for the limit of function ![]() again. The power law for limits [35] states that if we have
again. The power law for limits [35] states that if we have ![]() , for
, for ![]() , then
, then
![]()
What this law for limits is telling us is that any limit for an exponential function ![]() is equivalent to the limit of
is equivalent to the limit of ![]() , where the entire limit is placed to the power of
, where the entire limit is placed to the power of ![]() . This in turn means that the limit
. This in turn means that the limit ![]() as a result is put to the power of
as a result is put to the power of ![]() as well.
as well.
Example:
Let ![]() with
with ![]() . So if we are now given
. So if we are now given ![]() then we can find the following limit.
then we can find the following limit.
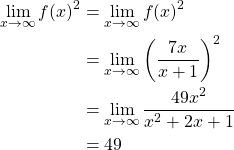
Now we can see here that ![]() , thus by the power law of limits
, thus by the power law of limits
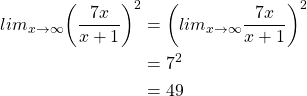
Root Law for Limits
Given ![]() the
the ![]() , for an odd
, for an odd ![]() , has a limit as
, has a limit as ![]() approaches
approaches ![]() of
of
![]()
for all ![]() if
if ![]() is even [35].
is even [35].
Just as we saw in the power law of limits. When we apply an operation to a function ![]() we see that the limit is effected in the same way the function is. As we see with the root law for limits, when we apply the operation square root to the function
we see that the limit is effected in the same way the function is. As we see with the root law for limits, when we apply the operation square root to the function ![]() we can also apply it to the limit. This law is helpful when we already know the limit result of
we can also apply it to the limit. This law is helpful when we already know the limit result of ![]() and are then given a problem which manipulates
and are then given a problem which manipulates ![]() in such a way.
in such a way.
Now consider ![]() and
and ![]() for all
for all ![]() over an open interval containing
over an open interval containing ![]() . Let
. Let ![]() and
and ![]() be real arbitrary numbers such that
be real arbitrary numbers such that ![]() and
and ![]() .
.
Sum Law for Limits
Given the terms above the sum law for limits states [35]:
![]()
Example:
Difference law for limits
Given the terms above the difference law for limits states [35]:
![]()
The difference law comes in handy especially when we already know the limits of ![]() and
and ![]() independently from one another. Just as we mentioned previously in the root law of limits when we are posed a problem that asks us to find the limit of a manipulated function, or in this case two functions, we can save time by applying the difference law of limits. Now, since we usually have to show our work, knowing the difference law helps us understand how to find the limit of
independently from one another. Just as we mentioned previously in the root law of limits when we are posed a problem that asks us to find the limit of a manipulated function, or in this case two functions, we can save time by applying the difference law of limits. Now, since we usually have to show our work, knowing the difference law helps us understand how to find the limit of ![]() . Many of these laws, rules, and axioms that we will cover are considered guidelines for how functions work together and independently under different operations.
. Many of these laws, rules, and axioms that we will cover are considered guidelines for how functions work together and independently under different operations.
Product Law for Limits
The product rule states [35]:
![]()
As mentioned under the difference law of limits when we apply an operation to ![]() and
and ![]() the limit is accordingly operated as well. These are the basic laws of limits, keep in mind that they are the fundamental rules for limits and operations on limits. Much of calculus consists of rules and application, so we may become proficient in knowing the abilities and limitations of applying operations, as well as the many methods for appropriately evaluating a function. Next, we will discuss derivatives and the various rules around differentiating functions appropriately.
the limit is accordingly operated as well. These are the basic laws of limits, keep in mind that they are the fundamental rules for limits and operations on limits. Much of calculus consists of rules and application, so we may become proficient in knowing the abilities and limitations of applying operations, as well as the many methods for appropriately evaluating a function. Next, we will discuss derivatives and the various rules around differentiating functions appropriately.
