3 Derivatives
We now move on to derivatives and the process in which we find derivatives, also called differentiation. The informal definition of a derivative is “the rate of change of a function with respect to a variable” [27]. This rate of change is also considered the slope of a tangent line to a function ![]() on an interval
on an interval ![]() containing
containing ![]() and is denoted by the difference quotient [35]
and is denoted by the difference quotient [35]
![]()
A derivative function of ![]() is denoted
is denoted ![]() and is considered differentiable at
and is considered differentiable at ![]() if
if ![]() exists. The resulting value is then considered the instantaneous rate of change of
exists. The resulting value is then considered the instantaneous rate of change of ![]() at
at ![]() . The derivative function
. The derivative function ![]() if defined on
if defined on ![]() results in the following limit [35]:
results in the following limit [35]:
![]()
In order to be able to apply this general limit, ![]() must pass the vertical line test. In order for a function to pass the vertical line test there must be no more than one value of
must pass the vertical line test. In order for a function to pass the vertical line test there must be no more than one value of ![]() in the range for each
in the range for each ![]() value in the domain on the defined interval for
value in the domain on the defined interval for ![]() ;
; ![]() must be one-to-one. There is an exception to this requirement which will be discussed in the later section on Implicit Differentiation.
must be one-to-one. There is an exception to this requirement which will be discussed in the later section on Implicit Differentiation.
From the previous section we know that in order for a limit to exist it must be continuous and therefore we introduce the following theorem for continuity in differentiation.
Theorem: Differentiability Implies Continuity
Let ![]() be a function and
be a function and ![]() be a random variable within the domain of
be a random variable within the domain of ![]() . If
. If ![]() is differentiable at
is differentiable at ![]() , then
, then ![]() is continuous at
is continuous at ![]() .
.
This theorem is vital to our knowledge of the limitations around differentiation. We can say that every differentiable function is continuous but that does not mean that every continuous function is differentiable. Now that we have been introduced to this theorem we can go forward into the rules of differentiation with the knowledge that each resulting function is continuous.
The Constant Rule
Let ![]() such that by the limit definition given above we have the following [35]:
such that by the limit definition given above we have the following [35]:
![]()
Now since ![]() is a constant function then
is a constant function then ![]() such that we have the following [35]:
such that we have the following [35]:
![]()
When we take the derivative of a constant we get ![]() , this is because when we take a derivative we are taking it with respect to a variable, for example
, this is because when we take a derivative we are taking it with respect to a variable, for example ![]() . When we have come down to only
. When we have come down to only ![]() we have reduced
we have reduced ![]() as much as possible and thus the last step is to take the derivative of
as much as possible and thus the last step is to take the derivative of ![]() , with respect to
, with respect to ![]() , to get the result of
, to get the result of ![]() . Thus when we take the derivative of
. Thus when we take the derivative of ![]() we simply are left with 0. This law is one of the fundamental rules that we all learn in calculus in order to understand how to apply differentiation in different problems.
we simply are left with 0. This law is one of the fundamental rules that we all learn in calculus in order to understand how to apply differentiation in different problems.
The Power Rule
The next rule we are going to see is needed to understand the examples given in the later rules. The power rule was previously mentioned as being first introduced by Gottfried Leibniz back in the mid 17th century. He stated [35]:
![]()
We will see the power rule utilized in a later example for the Constant Multiple Rule. For now we will take away that we are reducing our variable ![]() when we take the derivative of
when we take the derivative of ![]() with respect to
with respect to ![]() . As we mentioned, previously, under the constant rule when we take a derivative we are, in a way, reducing the variable with which we are differentiating with respect to. With the power rule we see how this is appropriately applied.
. As we mentioned, previously, under the constant rule when we take a derivative we are, in a way, reducing the variable with which we are differentiating with respect to. With the power rule we see how this is appropriately applied.
Extended Power Rule
The extended power rule is applied to functions whose exponent ![]() is a negative integer. Very similar to the power rule, the extended power rule states [35], if for all
is a negative integer. Very similar to the power rule, the extended power rule states [35], if for all ![]() where
where ![]() then for function
then for function ![]() it follows that
it follows that
![]()
Example:
Let ![]() which is equivalent to
which is equivalent to ![]() . If we apply the extended power rule
. If we apply the extended power rule ![]() is as follows
is as follows
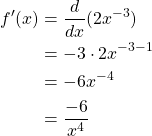
We can see from this example that the extended power rule is much like the power rule, utilizing the same process. The difference, here, being that our exponent, in this example ![]() , is a negative value and thus instead of differentiating
, is a negative value and thus instead of differentiating ![]() towards smaller and smaller exponents of
towards smaller and smaller exponents of ![]() we are increasing the absolute value of the exponent.
we are increasing the absolute value of the exponent.
The Constant Multiple Rule
The constant multiple rule states [35]:
![]()
such that ![]() and thus
and thus ![]() becomes
becomes ![]() .
.
We are somewhat familiar with the application of constants to functions. We previously saw in limits how a constant applied to a function effected the limit result. Here we see that we can extract constants from a function in order to simplify the differentiable function and thus reapply the constant to the derivative. In the following example we will see the full process for apply the constant multiple rule.
Example:
Given ![]() then
then ![]() which simplifies to
which simplifies to ![]() . Now let constant
. Now let constant ![]() , by the constant multiple rule the derivative of
, by the constant multiple rule the derivative of ![]() is
is
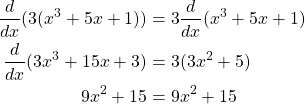
See how the constant ![]() was removed from the equation on the right hand side before we took the derivative of the function and then reapplied
was removed from the equation on the right hand side before we took the derivative of the function and then reapplied ![]() to the function. This example gives us a wonderful look at the comparison of the two ways for deriving our
to the function. This example gives us a wonderful look at the comparison of the two ways for deriving our ![]() . The left hand side provided us with the straight forward method, without the constant multiple rule. While the right hand side applied the constant multiple rule, all the while the two equations were equal throughout.
. The left hand side provided us with the straight forward method, without the constant multiple rule. While the right hand side applied the constant multiple rule, all the while the two equations were equal throughout.
The Sum Rule
Consider now two functions ![]() and
and ![]() . Let
. Let ![]() be defined as
be defined as ![]() . By the sum rule [35]:
. By the sum rule [35]:
![]()
Recall how limits were effected under operation addition, this same idea applies to derivatives. If we are adding together two functions, and then taking the derivative of the result, we can just as easily derive each function individually. In fact this is how differentiation works under addition. Each variable ![]() in a function is independently differentiated. As we will see in the following example, a function we once simply considered
in a function is independently differentiated. As we will see in the following example, a function we once simply considered ![]() in now partitioned into smaller equations summing up to
in now partitioned into smaller equations summing up to ![]() .
.
Example:
We have previously seen the example function ![]() . Let us now consider
. Let us now consider ![]() and let us define
and let us define ![]() and
and ![]() such that
such that ![]() . By the sum rule,
. By the sum rule,
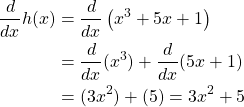
Now we move forward to the difference rule for derivatives.
The Difference Rule
Now consider if we have the same two equations ![]() and
and ![]() and let
and let ![]() . By the difference rule [35]
. By the difference rule [35]
![]()
Just as we saw in the sum rule for differentiation we apply the subtraction operation in the same manner.
The Product Rule
Let ![]() , by the product rule
, by the product rule
![]()
This rule provides us with the formatting for how we must take the derivative of a function comprised of the product of two functions. When faced with a problem such as this the method is to take the derivative of one function at a time, while leaving the other intact for the time being, before summing them up to give us the derivative of the total function ![]() . We see this rule applied in the following example.
. We see this rule applied in the following example.
Example:
Let ![]() and
and ![]() then
then ![]() and
and ![]() respectively. By the quotient rule we have the following.
respectively. By the quotient rule we have the following.
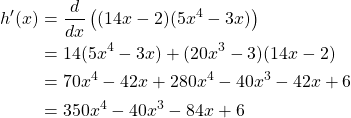
The Quotient Rule
Like the sum, difference, and product rule, the quotient rule is involved with differentiating a complex function composed of two or more smaller functions. The quotient rule is more complex [35].
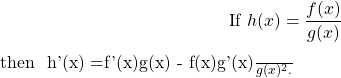
Without becoming proficient in the application of the quotient rule, we would be unable to derive functions, of the format ![]() , appropriately. Simply put the quotient rule tells us how a function, of this format, behaves under differentiation. We can see this rule applied in the following example.
, appropriately. Simply put the quotient rule tells us how a function, of this format, behaves under differentiation. We can see this rule applied in the following example.
Example:
Given the following equation
![]()
Consider ![]() and
and ![]() . Let us first take the derivative of
. Let us first take the derivative of ![]() and
and ![]() independently. We thus have
independently. We thus have ![]() and
and ![]() . Now we apply the quotient rule.
. Now we apply the quotient rule.
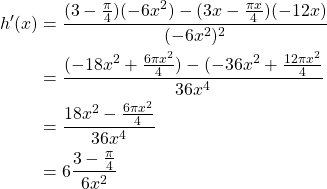
The Chain Rule
We will delve deeper into this rule in a later section but for now a brief introduction. Let ![]() be a function composed of a function inside another function represented by
be a function composed of a function inside another function represented by ![]() and
and ![]() respectively.
respectively.
This gives us ![]() . The chain rule states [35]
. The chain rule states [35]
![]()
Examples of the chain rule being applied will be provided later on in this chapter.
Implicit Differentiation
Briefly, implicit differentiation is the process of taking the derivative of an equation that does not pass the vertical line test. Early on in this chapter it was stated that in order for ![]() to be differentiable it must be a one-to-one function with one exception. In differentiable functions, there is an independent
to be differentiable it must be a one-to-one function with one exception. In differentiable functions, there is an independent ![]() variable in the domain and a dependent
variable in the domain and a dependent ![]() variable in the range for
variable in the range for ![]() for which
for which ![]() is written as a function of
is written as a function of ![]() . But in some cases we are given equations where
. But in some cases we are given equations where ![]() is not a function of
is not a function of ![]() and therefore requires implicit differentiation to be able to find the slope of a tangent line.
and therefore requires implicit differentiation to be able to find the slope of a tangent line.
3.1 Chain Rule
Recall from the previous section that the chain rule is applied when a function is comprised of two or more functions, one inside the next and so on. We can describe functions that qualify for using the chain rule as Russian dolls. Just as a Russian doll contains many smaller dolls within each outer shell, a function requiring the chain rule has an outermost function that contains many more functions within each other. As stated previously under the chain rule if ![]() then
then ![]() . In order to find the derivative of
. In order to find the derivative of ![]() we begin by finding the derivative of the outermost function, making no changes to the functions contained within, we then take the derivative of the next outermost function and multiply it to the previously found derivative. This process is repeated until all layers have been derived in this pattern. Let us consider some examples.
we begin by finding the derivative of the outermost function, making no changes to the functions contained within, we then take the derivative of the next outermost function and multiply it to the previously found derivative. This process is repeated until all layers have been derived in this pattern. Let us consider some examples.
Example:
Let ![]() , consider
, consider ![]() and
and ![]() then by the chain rule
then by the chain rule
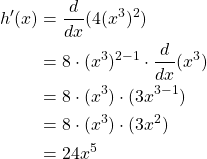
Consider, now, some trigonometric functions using chain rule.
Example:
Given ![]() here we have
here we have ![]() and
and ![]() . Below are the steps to solve for
. Below are the steps to solve for ![]() using the chain rule.
using the chain rule.
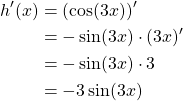
Example:
Now consider the equation ![]() in this case we have
in this case we have ![]() ,
, ![]() , and
, and ![]() . We will use the chain rule, trigonometric derivatives, and the power rule to solve for
. We will use the chain rule, trigonometric derivatives, and the power rule to solve for ![]() .
.
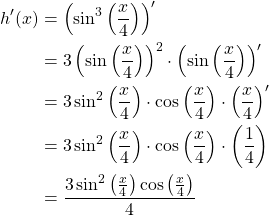
3.2 Implicit Differentiation
We now move to a form of differentiation with the purpose of finding the slope of a tangent line for a function that clearly does not pass the vertical line test. Most equations we see have a dependent variable ![]() and an independent variable
and an independent variable ![]() where
where ![]() is expressed in terms of
is expressed in terms of ![]() . But there are certain equations, for example
. But there are certain equations, for example ![]() , where
, where ![]() is not a function of
is not a function of ![]() but for which a tangent line slope can still be derived. In cases such as these we must use implicit differentiation. The derivative of an equation requiring implicit differentiation is usually denoted in the form
but for which a tangent line slope can still be derived. In cases such as these we must use implicit differentiation. The derivative of an equation requiring implicit differentiation is usually denoted in the form ![]() .
.
There are generally 3 steps to solving an integral using implicit differentiation [35]:
- Take the derivative,
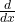 , of both sides of the equation.
, of both sides of the equation. - Rewrite the equation such that the terms with
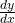 are on the left hand side.
are on the left hand side. - Solve for
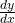 .
.
Example:
Given ![]() and
and ![]() such that
such that ![]() . We first differentiate both sides of the equation giving us
. We first differentiate both sides of the equation giving us ![]() . Using the constant and sum rules for differentiation we have the following.
. Using the constant and sum rules for differentiation we have the following.
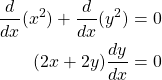
Subtracting ![]() from both sides we find the following result.
from both sides we find the following result.
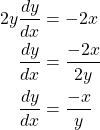
Example:
Given ![]() using implicit differentiation.
using implicit differentiation.
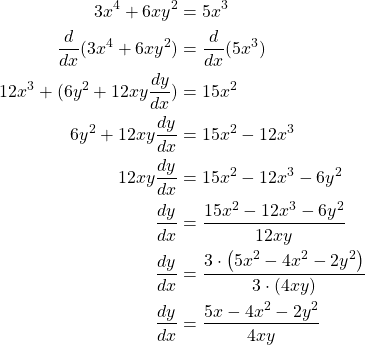
It can be see above that to solve for ![]() we must first differentiate
we must first differentiate ![]() and
and ![]() with respect to
with respect to ![]() and then moving all terms with
and then moving all terms with ![]() to the left and solve for
to the left and solve for ![]() . Thus concludes this section on implicit differentiation.
. Thus concludes this section on implicit differentiation.
