5 Application
Calculus provides some of the most integrated mathematics concepts in the world. On a day to day basis various jobs across the world require the use of methods taught in calculus to build structures, test safety equipment, calculate the vastness of space, track the spread of disease, etc. The formal terms used in calculus for such applications consist of velocity, work, optimization, and related rates to name a few. There is a reason calculus is broken up into so many sections and even then, there are courses offered around the world that focus on only one subcategory of calculus per semester or quarter.
Related rates and work are some of my favorite applications in calculus methods.
When we are first introduced to related rates the concept can seem exhausting and frustrating but once the patterns are found related rates can be applied to a multitude of problems within the classroom as well as in real life. Once related rates is mastered they truly are fun and can easily be used to calculate distance, speed, or volume given related values that are already known.
The second application to be discussed is calculations revolving around work. This concept comes very easy to most and I wish to provide an introduction here because I feel it is a topic that is briefly covered in calculus but has so many vital applications in scientific testing and engineering. As an outdoor athlete I require lots of equipment and rigging techniques to keep me safe. Each piece of equipment I need must go through constant redesign and testing before being put on the market for people like me to utilize safely. In my adventures outside I need to consider force and work required when choosing what equipment and rigging techniques to implement to keep myself and my team safe and efficient as well as save energy. Although I am not computing work required in each of these situations the idea is still there even if the numbers are not and that fascinates me.
5.1 Related Rates
We have already been introduced to derivatives and integrals, key components for calculating related rates. The world is full of constantly moving matter changing with respect to time. Any object with related quantities also has related rates with respect to time. An example is a balloon, which has a value for volume and a value for radius; we call these related quantities. When a balloon begins to inflate or deflate the derivative of the volume with respect to time gives us the rate of change of the volume and the derivative of the radius with respect to time gives us the rate of change of the radius; we call these related rates [35]. In calculus class, problems are usually posed where, given one known rate and the distance between two related quantities, we are asked to find the rate of change of a related quantity at time ![]() .
.
One of the most popular examples of this type of problem is the Hot Air Balloon problem, which we will see an example of below.
Example:
A hot-air balloon is 70 ft above the ground when a motorcycle, traveling in a straight line on a road horizontal to the line of the hot air balloon, passes underneath going 40 miles per hour. Let the balloon rise vertically at a rate of 6 feet per second. Find the rate of change of the distance between the hot-air balloon and the motorcycle after 12 seconds?
Let us consider a triangle with the sides x, y, and z. Let the base of the triangle, ![]() , be representative of the horizontal distance between the hot-air balloon and the motorcycle. Let opposite side length,
, be representative of the horizontal distance between the hot-air balloon and the motorcycle. Let opposite side length, ![]() , represent the vertical distance between the hot-air balloon and the ground. Then the hypotenuse,
, represent the vertical distance between the hot-air balloon and the ground. Then the hypotenuse, ![]() , is representative of the direct distance between motorcycle and hot-air balloon. We must first give an equation to represent
, is representative of the direct distance between motorcycle and hot-air balloon. We must first give an equation to represent ![]() and
and ![]() as they relate to one another. We have the following
as they relate to one another. We have the following
![]()
Next let the rate of change with respect to time ![]() for
for ![]() ,
, ![]() , and
, and ![]() be denoted
be denoted ![]() ,
, ![]() and
and ![]() respectively. Using implicit differentiation we take the derivative of the above expression.
respectively. Using implicit differentiation we take the derivative of the above expression.
![]()
We know from the information given in the problem that ![]() has a rate of change of 40 miles per hour. We convert this rate to feet per second by the following calculation.
has a rate of change of 40 miles per hour. We convert this rate to feet per second by the following calculation.
![]()
Thus we know that ![]() and
and ![]() . Next we know at time
. Next we know at time ![]() the balloon was 70 feet of the ground, we can calculate the distance
the balloon was 70 feet of the ground, we can calculate the distance ![]() at time
at time ![]() by the following
by the following
![]()
We can also calculate the distance ![]() , knowing the motorcycle moves at a rate of
, knowing the motorcycle moves at a rate of ![]() feet per second.
feet per second.
![]()
From our original expression relating our variables we can solve for the distance ![]()
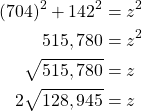
Now we can substitute our found values into our differentiated expression
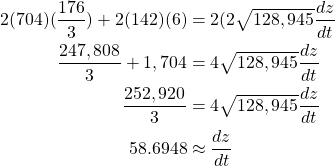
We give an approximation for the rate of change for ![]() as we rounded the answer to four decimal places.
as we rounded the answer to four decimal places.
This concludes the section on related rates. We have seen that through differentiation and related quantities we are able to calculate an unknown distance or the instantaneous rate of change at ![]() . This example is only one of many that prove how related rates can help to find any related value within a system such as the one given in our hot-air balloon example.
. This example is only one of many that prove how related rates can help to find any related value within a system such as the one given in our hot-air balloon example.
5.2 Work
We now move to the second application of calculus to be discussed in this chapter, work. We see work every day, we see work when we push a button or stretch a rubber band. In calculus work is associated with force as the amount of energy required by force to move an object in some way [35]. Not just any notation can be used here which is why work is most commonly given in units of newton-meters or joules ![]() . In order to calculate the value of work given a certain amount of force or a related rate of work we need to use integration. We use integration when calculating work because rarely is it possible that constant force is applied to an object. This is why we define work by the following integral [35].
. In order to calculate the value of work given a certain amount of force or a related rate of work we need to use integration. We use integration when calculating work because rarely is it possible that constant force is applied to an object. This is why we define work by the following integral [35].
![]()
Here ![]() is representative of the equation for the force required to move an object. In work problems it is not uncommon for
is representative of the equation for the force required to move an object. In work problems it is not uncommon for ![]() and for
and for ![]() . This represents the direction of motion for the object. If we have an already stretched out rubber band and wish to calculate the work required to un-stretch or compress the band then our starting point will be greater than our ending point on the interval.
. This represents the direction of motion for the object. If we have an already stretched out rubber band and wish to calculate the work required to un-stretch or compress the band then our starting point will be greater than our ending point on the interval.
Consider an example to illustrate this idea. A common type of problem given to calculate work involves springs.
Example:
Hooke’s Law states that ![]() where
where ![]() is a constant.Consider a spring, let it take 8N to stretch the spring from its equilibrium point to 0.5m. How much work is done to stretch the spring 0.7m from equilibrium?
is a constant.Consider a spring, let it take 8N to stretch the spring from its equilibrium point to 0.5m. How much work is done to stretch the spring 0.7m from equilibrium?
Using Hooke’s law let
![]()
Thus we have the expression for force given as ![]() . Now we can solve for the integral from
. Now we can solve for the integral from ![]() to
to ![]() with
with ![]() .
.
![]()
Thus we can conclude that the amount of work required to stretch a spring from its equilibrium to ![]() is
is ![]() .
.
This concludes our topic on work. In the next section we cover multi-variable calculus which, much like what we saw in implicit differentiation, involves more than just one variable ![]() .
.
