6 Multivariate Calculus
Multi-variable calculus is just that, multi-variable. Most expressions we have looked at in this chapter thus far involve a single variable at a time. Multi-variable calculus uses two or more variables in an expression. Where a single variable function may be denoted ![]() , a multi-variable function maybe denoted
, a multi-variable function maybe denoted ![]() . We have seen an example of this kind of expression in implicit differentiation where we were shown an example of a function involving both
. We have seen an example of this kind of expression in implicit differentiation where we were shown an example of a function involving both ![]() and
and ![]() where
where ![]() was not dependent upon
was not dependent upon ![]() .
.
Multivariable calculus can involve calculations using 3D models, planes, or vectors instead of 2D graphs. The differentiation of these kinds of expressions require a unique method known as partial differentiation.
6.1 Partial Differentiation
As explained above, partial differentiation is used to take the derivative of a multivariable function with respect to one variable. We call this partial differentiation because you are treating all other variables as constants and therefore are only finding the derivative with respect to one of the many variables that make up the function.
The basic concept for taking a partial derivative with respect to one variable is to treat all other variables as constants.
Example:
Take the partial derivative with respect to ![]() of
of ![]() .
.
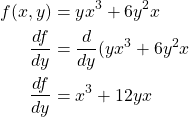
Thus we conclude that the partial derivative with respect to ![]() for
for ![]() is
is ![]() .
.
We saw in that example that when taking the derivative with respect to ![]() we treated the variable
we treated the variable ![]() as a constant associated with
as a constant associated with ![]() . This is the fundamental idea behind partial differentiation.
. This is the fundamental idea behind partial differentiation.
