7 Sequences and Series
Sequences and series are very much intertwined with one another. Sequences alone are one concept and series are based off the idea of summing the values of a sequence in order to construct a series. We will break these two concepts into their own sections and address each individually.
7.1 Sequences
We begin this section by discussing sequences.
Definition.
A sequence ![]() of real numbers is a function
of real numbers is a function ![]() , where
, where ![]() .
.
In short a sequence“is a function whose domain is a set of consecutive natural numbers beginning with 1″[19]. Some sequences are a set number of values long, called finite sequences, where as others are infinitely long, we call these infinite sequences. When we consider what a sequence looks like we imagine an expression representing the general term for the sequence. This general term is usually represented by ![]() . Observe the following finite sequence example.
. Observe the following finite sequence example.
Example:
Let ![]() find the first 3 terms of the sequence.
find the first 3 terms of the sequence.
![]()
![]()
![]()
Now there are some sequences that utilize the value of the last term to calculate the value of the next. We call this a recurrence relation. One example of this type of sequence is the Fibonacci sequence where ![]() . We see in this sequence that the two previous terms are used to calculate the value of the next term. We can observe sequences to find trends and from this we can conclude if a sequence converges or diverges. This will allow us to dictate if a sequence is reaching a quantifiable limit or not. We will define convergence and divergence later on in this section.
. We see in this sequence that the two previous terms are used to calculate the value of the next term. We can observe sequences to find trends and from this we can conclude if a sequence converges or diverges. This will allow us to dictate if a sequence is reaching a quantifiable limit or not. We will define convergence and divergence later on in this section.
7.2 Series
Moving on from sequences to series. We define a series as a formal expression for the sum of the terms of a sequence. We usually denote this as
![]()
When we expand this notation we get the following calculation:
![]()
There are various general series we come across in calculus [19]:
Arithmetic Series
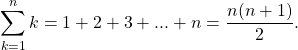
This series is very straight forward, we have the sum of values starting from ![]() with the following value increasing by 1. Now we may have a manipulated version of this series which converts every other value to a negative. This type of series is categorized as an alternating series but it should be noted that an arithmetic series will not always directly follow this pattern and can easily be altered in various ways. Much like our other section under calculus we are given the structure of basic formulas, with the knowledge that these series will have alterations applied which will effect the results.
with the following value increasing by 1. Now we may have a manipulated version of this series which converts every other value to a negative. This type of series is categorized as an alternating series but it should be noted that an arithmetic series will not always directly follow this pattern and can easily be altered in various ways. Much like our other section under calculus we are given the structure of basic formulas, with the knowledge that these series will have alterations applied which will effect the results.
Harmonic Series
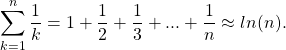
As we can see by observing the trend of the harmonic series there is an increase in the denominator such that the values being added to the sum total are getting smaller and smaller. Now of course there are many version of the harmonic series. We can change the value of he numerator, or we can place ![]() to a power of some natural number.
to a power of some natural number.
Geometric Series
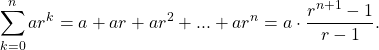
With the geometric series we are considering the terms to be a constant ![]() multiplied by the preceding term
multiplied by the preceding term ![]() . In a general form the series appears as
. In a general form the series appears as
![]()
If the value for ![]() is greater than one then the series will trend to infinity in which we conclude that the series diverges. We will discuss divergence and convergence shortly. If
is greater than one then the series will trend to infinity in which we conclude that the series diverges. We will discuss divergence and convergence shortly. If ![]() is less than negative 1 then the series will appear to alternate between positive values and negative values and again we say the series diverges. Only when
is less than negative 1 then the series will appear to alternate between positive values and negative values and again we say the series diverges. Only when ![]() does a geometric series converge [19]. There is a different notation for this situation given as
does a geometric series converge [19]. There is a different notation for this situation given as
![]()
Example:
Let ![]() we have the following geometric series
we have the following geometric series
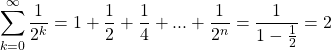
The Power Series
With the example for geometric series in mind we introduce the power series [19]. A power series is any series taking on the form
![]()
We see it is called the power series because of the expression containing a higher power variable [19]. Now not every power series needs to be centered around 0 in which case they are centered around some ![]() denoted as
denoted as
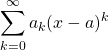
What we mean when discussing a series being centered around ![]() or
or ![]() is that every series has an interval. We assume the interval is centered at
is that every series has an interval. We assume the interval is centered at ![]() if it is not specified otherwise. When a series is centered at
if it is not specified otherwise. When a series is centered at ![]() then we need to account for this within the formula for the series which is why we include the vital piece
then we need to account for this within the formula for the series which is why we include the vital piece ![]() in the expression otherwise the series will act like it is centered around
in the expression otherwise the series will act like it is centered around ![]() and your sum will be incorrect for the interval centered at
and your sum will be incorrect for the interval centered at ![]() .
.
7.3 Convergence and Divergence
Before we can go any further we need to discuss divergence and convergence. It has already been brought up in our discussion of limits of a sequence and in our discussion on geometric series but we will explain this further. Divergence and convergence of a series help to define the trend of a series. We calculate convergence and divergence of a sequence through partial sums. Partial sums are the sums of sections of series, observe the following example.
Example:
Consider the series
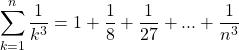
The first three partial sums are as follows
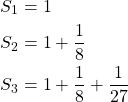
Here we see that we are taking small portions of the values for the series and summing them up as partial sums to the series. With this in mind we define a series to be convergent if the limit for the sum of the series approaches a quantifiable limit. For some finite series this simply requires finding the total sum of the series. In order to quantify the convergence of an infinite series we use the limit convergence of the partial sums to determine if an infinite series converges. Conversely, a series diverges if limit cannot be calculated. Thus we can say any series or sequence that does not converge, diverges. Consider the two examples below.
Example:
Consider the series
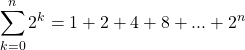
To determine the convergence or divergence of the series we take the limit as ![]() approaches
approaches ![]() .
.
![]()
As ![]() approaches
approaches ![]() we see that
we see that ![]() grows without bound and thus we can conclude that the series diverges.
grows without bound and thus we can conclude that the series diverges.
This is an example of a series which diverges which ultimately means no limit can be reached because the series will continue to grow infinitely larger as ![]() approaches infinity. Consider now an example of a convergent series.
approaches infinity. Consider now an example of a convergent series.
Example:
Consider the series
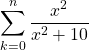
To find if the series converges or diverges we take the limit as ![]() approaches infinity.
approaches infinity.
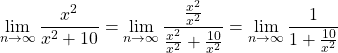
We see that as ![]() approaches
approaches ![]() ,
, ![]() approaches 0 since the numerator stays constant while the denominator grows without bound. Thus we can calculate the limit to be as follows
approaches 0 since the numerator stays constant while the denominator grows without bound. Thus we can calculate the limit to be as follows
![]()
Thus we can conclude that the series converges to 1 given that the limit as ![]() approaches infinity is 1.
approaches infinity is 1.
7.4 Series Tests
Now that we have covered convergence and divergence of a series we can briefly cover the different tests for convergence or divergence. It should be noted that these tests exist because not all series are as easy to test for as the examples given in the last section.
Integral Test
Let ![]() be a continuous, positive, and decreasing function on the interval from 1 to infinity [8]. Let us define
be a continuous, positive, and decreasing function on the interval from 1 to infinity [8]. Let us define ![]() for a series then
for a series then
![]()
What this means is that if the integral for ![]() from
from ![]() to infinity converges then the series for
to infinity converges then the series for ![]() on the same interval, converges and vice verse. We apply this to an example.
on the same interval, converges and vice verse. We apply this to an example.
Example:
Let ![]() be our series such that
be our series such that ![]() . We can note here that
. We can note here that ![]() is positive, continuous on the interval
is positive, continuous on the interval ![]() and decreasing. Thus we apply the integral test to test for convergence.
and decreasing. Thus we apply the integral test to test for convergence.
![]()
Now we cannot just substitute infinity for ![]() and solve we need to take the limit as
and solve we need to take the limit as ![]() approaches infinity for
approaches infinity for ![]() and solve for the limit.
and solve for the limit.
![]()
Solving for the limit we see as ![]() approaches infinity,
approaches infinity, ![]() approaches
approaches ![]() . Thus we say the limit approaches
. Thus we say the limit approaches ![]() giving us the following result for the integral.
giving us the following result for the integral.
![]()
Thus we conclude that the integral converges and thus the series ![]() also converges by the integral test.
also converges by the integral test.
The Comparison Test
If we have two series, ![]() and
and ![]() where
where ![]() for all values of
for all values of ![]() then by the comparison test we have the following rules [8].
then by the comparison test we have the following rules [8].
- Let
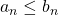 , if
, if 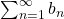 converges, then
converges, then 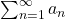 converges.
converges. - Let
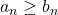 , if
, if 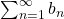 diverges, then
diverges, then 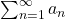 diverges.
diverges.
In the first rule we see that if the expression ![]() is greater than
is greater than ![]() and the series for
and the series for ![]() converges, then all series smaller than
converges, then all series smaller than ![]() , including
, including ![]() also converge. And following this, the second rule tells us that if a smaller expression
also converge. And following this, the second rule tells us that if a smaller expression ![]() diverges then a greater expression
diverges then a greater expression ![]() must also diverge.
must also diverge.
The Limit Comparison Test
The limit comparison test uses the same concept of comparing convergence or divergence between two series. For the limit comparison tests we again let ![]() for all values of
for all values of ![]() . Then the following rules are given [8].
. Then the following rules are given [8].
- If
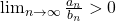 , then
, then 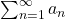 converges
converges 
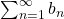 converges.
converges. - If
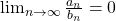 and
and 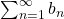 converges, then
converges, then 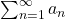 converges.
converges. - If
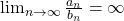 and
and 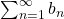 diverges, then
diverges, then 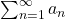 diverges.
diverges.
What these rules equate to is very similar to the comparison tests, depending on the value of ![]() being greater or less than
being greater or less than ![]() and divergent or convergent then
and divergent or convergent then ![]() will also be divergent or convergent respectively.
will also be divergent or convergent respectively.
The Alternating Series Test
The alternating series test involves series which alternate between positive and negative values. Consider the example ![]() . The series would look like the following
. The series would look like the following
![]()
We can see in this example that the series alternates from positive values to negative values depending on ![]() . In order to test for convergence of a series of this kind we are given the following rule [8].
. In order to test for convergence of a series of this kind we are given the following rule [8].
Let ![]() for all values of
for all values of ![]() . If
. If ![]() is decreasing then
is decreasing then
![]()
Consider the following example.
Example:
Consider the series ![]() . Let
. Let ![]() , if we take the limit of
, if we take the limit of ![]() we get the following.
we get the following.
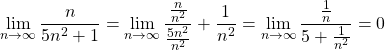
Thus we can conclude that ![]() and we can conclude that the series
and we can conclude that the series
![]()
Converges by the alternating series test.
The alternating series test can also be proven absolutely through the next test we are going to discuss.
The Absolute Convergence Test
This next test is quite straight forward and relates to the alternating series test in the sense that instead of finding the limit for a related series we simply take the absolute value of the series to test for convergence. If ![]() converges, then
converges, then ![]() converges [8].
converges [8].
If we consider the alternating series test in which ![]() is defined as
is defined as ![]() and we take the absolute value for
and we take the absolute value for ![]() we get
we get
![]()
There are more technical comparison tests used to solve complex series problems but for now we will only focus on the tests provided above. Moving onto the next section we will delve deeper into differential equations than what has been provided in the derivatives section of the chapter.
