Difference Equations

Maggie Schildt

41 Difference Equations

We have a general understanding of a basic model, now we can explore the relationship between two models which we call a system of difference equations. A common example of a system of difference equations is the predator prey model. We begin with a model for the population of a predator which is dependent upon the population of it’s prey. Vice versa, we have a model for the population of the prey which is dependent upon the population of the predator. What we look for in solving the system is to see if we are approaching an equilibrium value, and if the values remain close or if they do not. This can allow us to predict the long-term behavior of the system. We will utilize the predator-prey scenario in our next example.

Example:

Suppose the spotted owl’s primary food source is a single mouse. An ecologist wishes to predict the population level of the spotted owls and mice in a wildlife sanctuary. Let $M_{n}$ represent the mouse population after $n$ years. Let $O_{n}$ represent the owl population [9]. We are given the suggested model.

$\begin{equation*} M_{n+1}=1.2M_{n}-0.001O_{n}M_{n}, \ \ O_{n+1}=0.7O_{n}+0.002O_{n}M_{n} \end{equation*}$

We need to find the equilibrium point if there is one for this system.If we let $M_{n+1}=M_{n}$ and $O_{n+1}=O_{n}$ then we can rewrite our model and solve for the equilibrium value by simple algebra.

$\begin{equation*} \begin{split} M&=1.2M-0.001OM\\ M&=M(1.2-0.001O)\\ \end{split} \end{equation*}$

Now, we divide both sides by $M$ , then subtract $1.2$ from both sides and solve for $O$ .

$\begin{equation*} \begin{split} 1&=1.2-0.001O\\ -0.2&=-0.001O\\ 200&=O \end{split} \end{equation*}$

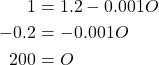
Now that we have found the value for owl population we can calculate the population of mice. We begin by substituting $200$ for $O$ and then simplifying to find $M$ .

$\begin{equation*} \begin{split} O&=0.7O+0.002OM\\ 200&=0.7(200)+0.002(200)M\\ 200&=140+0.4M\\ 60&=0.4M\\ 150&=M \end{split} \end{equation*}$

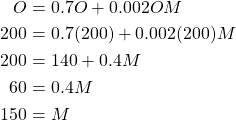
What this tells us is that if we start with population $(O, M)=(200,150)$ then the system will remain here, this is our equilibrium point. If we were to test other starting values we may see that the populations do not stay close together, if this is the case then we say that this system is unstable because any population values other than our initial equilibrium value and one population may completely diminish.

From systems of difference equations we move on to decision theory, where we focus on using models to measure the risk of different options under a decision.

41 Difference Equations

License

Share This Book