Euclidean Algorithm

Maggie Schildt

32 Euclidean Algorithm

We begin by introducing the greatest common divisor before following with the Euclidean Algorithm [28].

Definition. Greatest Common Divisor

Let $a,b\in \mathbb{Z}$ be positive and neither $a$ nor $b$ are equal to 0. The greatest common divisor of (a,b) is the largest positive integer that divides both $a$ and $b$ .

Theorem: Euclidean Algorithm

Suppose $a,b\in \mathbb{Z}$ such that $a\neq 0$ and $b\neq 0$ , then there are integers $x$ and $y$ such that $(a,b) = ax+by$ .

Example:

Find the $gcd (a,b)$ for the following pairs of integers, using the Euclidean algorithm. $a=40$ , $b=148$ [28].

$\begin{equation*} \begin{split} 148&=40 \cdot 3 + 28\\ 40&=28 \cdot 1 +12\\ 28&=12 \cdot 2 + 4\\ 12&=4 \cdot 3 + 0 \end{split} \end{equation*}$

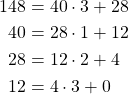
Thus we have found $gcd(40, 148) = 4$

Now there is an expanded version of the Euclidean algorithm but for time’s sake we will leave it at just the shortened definition with the example. We are actually quite familiar with this idea of the greatest common divisor as we were required to find the gcd in a few examples in the previous section on Modern Algebra. In this section we use the concept of the greatest common divisor to introduce two vital theorems associated with solving linear congruence problems.

Theorem:

Let $a,b\in \mathbb{Z}$ both be positive. Let $d$ be the gcd of $a$ and $m$ for $m\in \mathbb{Z}$ . The equation $ax=b (\mod m)$ has a solution if and only if $d$ divides $b$ . When $d$ dived $b$ , the equation has exactly $d$ solutions in modulus $m$ . [12]

Theorem:

Let $d$ be the gcd of positive integers $a$ and $m$ . The congruence $ax=b (\mod m)$ has a solution if and only if $d$ divides $b$ . When this is the case, the solutions are the integers in exactly $d$ distinct classes modulus $m$ .[12]

Example:

Describe all solutions of the given congruence, $36x = 15 (\mod 24)$

Firstly we can simplify $36x = 15 (\mod 24)$ , we know that $24$ fits into $36$ once so if we subtract $24$ from $36$ we should get the remainder $12$ . Thus we can rewrite our congruence as $12x = 15 (\mod 24)$ now let $d= gcd(12, 24)$ we know $d=12$ because the divisors of 12 are 1,2,3,4,6,12 and the divisors of 24 are 1,2,3,4,6,8,12,24 and as we can see the greatest common divisor is 12. Utilizing theorem 2.12 let $d=12$ and $b=15$ , since 12 cannot divide 15 we conclude that there are no solutions for $36x = 15 (\mod 24)$ .

This last example emphasizes the power of these theorems. We are able to apply theorems in order to skip attempting infinite possible solutions only to come to the same conclusion that there are no solutions to the given congruence.

32 Euclidean Algorithm

License

Share This Book