Functions

Maggie Schildt

15 Functions

We see functions all across mathematics, they are what most people think of when someone says “math” usually we are focusing on the content of a function and how to ascertain the solution to a function or the value for an unknown variable. Just like sets and relations can be classified, so can functions.

In the realm of relations we can say the functions are a set of relations. By definition, a function is “an expression, rule, or law that defines a relationship between an independent variable and a dependent variable”[27]. The relations involved with functions are what map the independent variable, say $x$ , to the dependent variable, say $y$ , and it should be noted that for each $x$ value there is only one $y$ value, there cannot be multiple results for $y$ using one specific $x$ value in the function $f(x)$ . We delve deeper into this topic in the subsections for one-to-one and onto, below.

13.1 One-to-one

We described this idea in functions where for every $x$ there is only one $y$ , this leaves an opening for different values of $x$ in $f(x)$ to result in the same $y$ values which is fine for a general function.

If a function is to be considered one-to-one or injective then it follows the following definition [31].

Definition. One-to-one

Given function $f$ with $X$ mapping to $Y$ , $X\rightarrow Y$ , $f$ is one-to-one if for $x_{1},x_{2}\in X$ , $f(x_{1})=f(x_{2})$ such that $x_{1}=x_{2}$ and no element in $Y$ is the image of more than one element in $X$ .

We mention, in the definition, this concept of mapping, illustrated by using arrows, $``\rightarrow"$ . Mapping is essentially the action of solving the function for some value $y$ , we input an $x$ value into function $f$ and solve for some value of $y$ , $x\rightarrow y$ . Observe, below, an illustration of mapping with a function.

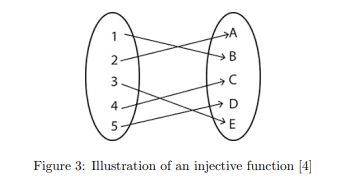
We see clean mapping from $x$ value to one $y$ value; for each $x$ there is only one $y$ and for each $y$ only one $x$ . If this were an illustration for a general function that did not qualify as one-to-one then we would have seen multiple $x$ values mapping to the same $y$ values. Now we will consider some general functions and test a few for the one-to-one property.

Example:

Prove that the inverse of a one-to-one function, is one-to-one [20].

Proof: Let $f:A\rightarrow B$ be a one-to-one function, then there is $x_{1}, x_{2}\in A$ such that $f(x_{1})=f(x_{2})$ which can be simplified, no matter the operations in $f$ , to find $x_{1}=x_{2}$ and thus we have found that $x_{1}\rightarrow f(x_{1})$ . From this last step we proved that no more than one $x\in A$ can map to a single element in $B$ . Now, by definition of an inverse function $f^{-1}(f(x))=x$ so for $f(x_{1}), f(x_{2})\in B$ it follows that $f^{-1}(f(x_{1}))=f^{-1}(f(x_{2}))$ which implies that $x_{1}=x_{2}$ . As we see here only one $x$ can map to an element in $B$ therefore we can conclude that $f^{-1}$ is one-to-one.

Now that we have an idea of one-to-one functions lets consider another category, onto functions also known as surjective functions.

13.2 Onto

Definition.

A function $f$ with $X$ mapping to $Y$ is considered onto if for all $y\in Y$ there is an $x\in X$ such that whenever $f(x)=y$ , all elements of $Y$ are used.

Lets look at an illustration of this to better understand an onto function.

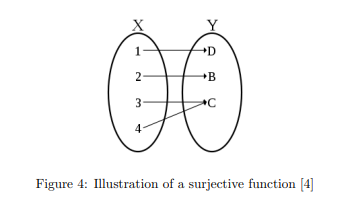
As we can see here, the characteristics of one-to-one and onto do not always go hand in hand. As long as every element in the right-hand, $Y$ , is mapped from an input $x$ on the left-hand side, $X$ , then the function $f$ is an onto function.

Example:

Suppose $f: A\rightarrow B$ and $g: B\rightarrow C$ are functions. Prove that if $g\circ f$ is one-to-one then $f$ is one-to-one. Prove that if $g\circ f$ is onto then $g$ is onto.

Firstly, if $g \circ f$ is one-to-one then there is $a,b\in A$ such that $f(a)=f(b)$ . For $g\circ f$ we find $g(f(a))=g(f(b))$ where $g(f(a))=(g\circ f)(a)$ and $g(f(b))=(g\circ f)(b)$ . We can rewrite our equivalence as $(g\circ f)(a)=(g\circ f)(b)$ . Thus, $a=b$ since $g\circ f$ is one-to-one which means that $f(a)=f(b)$ results to $a=b$ . Therefor $f$ is one-to-one.

Now, if $g\circ f$ is onto then there is an arbitrary $c\in C$ and $a\in A$ for which

$\begin{equation*} c=(g\circ f)(a)=g(f(a)) \end{equation*}$

Let there be $b\in B$ such that $b=f(a)$ and therefor

$\begin{equation*} c=g(f(a))=g(b) \end{equation*}$

Therefore we can conclude that $g$ is onto.

This example is a nice taste of one-to-one and onto relations because we can see how they can relate to expanded functions, not just a basic linear function $f(x)$ . There are some functions which satisfy both one-to-one and onto relations. We can classify a linear function that is both one-to-one and onto as a bijection or one-to-one correspondence.

Now that we have established the characteristics of functions in Bridge to Abstract Math lets move on to cardinality, the final section covered in this course. Keep in mind this idea of one-to-one correspondence, bijective, functions as we move into the next section as well.

15 Functions

License

Share This Book