25 Groups
Before we begin our discussion on groups we first need to define a binary operation. We are already familiar with addition, subtraction, multiplication, and division. When we have a binary operation in abstract algebra, we know that it is a function which takes two values to return only one. We begin by defining the operator [22].
Definition. Binary Operator
Given non empty set ![]() , a binary operator
, a binary operator ![]() is a rule which takes in two elements
is a rule which takes in two elements ![]() and outputs a single, non-distinct, element
and outputs a single, non-distinct, element ![]() .
.
There are many different binary operators in abstract algebra and our focus in this course was to study the structures created from different binary operations. There are different classifications for binary operations and one of the most fundamental is the understanding of closed binary operations [12].
Definition. Closed Binary Operation
A binary operation ![]() is an operation that applies to two values,
is an operation that applies to two values, ![]() and
and ![]() . A binary operation on a non-empty set
. A binary operation on a non-empty set ![]() can be mapped as
can be mapped as ![]() such that
such that ![]() is defined on every pair of elements in
is defined on every pair of elements in ![]() . As well,
. As well, ![]() uniquely associates each pair of elements in
uniquely associates each pair of elements in ![]() to some element in
to some element in ![]() .
.
Consider ![]() this function takes two real numbers and outputs a different, single, real number. This is an example of a closed binary operation because the output is an element of the set. We are also given the following theorem for the binary operation
this function takes two real numbers and outputs a different, single, real number. This is an example of a closed binary operation because the output is an element of the set. We are also given the following theorem for the binary operation ![]() on the set
on the set ![]() .
.
Theorem:
Consider the set of all integers ![]() , and the binary operation
, and the binary operation ![]() . If
. If ![]() then
then ![]() . Therefore,
. Therefore, ![]() is closed under multiplication.
is closed under multiplication.
We are familiar with the associative and commutative axioms from our previous section on Real Analysis. We will need to recall these definitions in order to understand binary operations in abstract algebra [12].
Definition. Associative Binary Operation
A binary operation is considered to be associative if ![]() for all
for all ![]() ,
, ![]() , and
, and ![]() in set
in set ![]() .
.
Definition. Commutative Binary Operation
A binary operation is considered commutative if ![]() for all
for all ![]() and
and ![]() in the set
in the set ![]() .
.
There are some binary operations that utilize tables in a way many may not have been familiar with before hand bur which are extremely fun to use. Some binary operations are defined by a table of elements and their associated results. We can see a good example here.
Example:
Given the commutative table below

Let the binary operation ![]() be defined by the rules given in the table then we produce a few of the following calculations.
be defined by the rules given in the table then we produce a few of the following calculations.
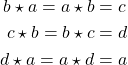
Moving from binary operations to complex numbers; we were first introduced to complex numbers when we discovered the existence of imaginary numbers, ![]() , to solve complex problems like
, to solve complex problems like ![]() where we let
where we let ![]() . Imaginary numbers do not exist within the set of real numbers, that is why we have the set
. Imaginary numbers do not exist within the set of real numbers, that is why we have the set ![]() which represents the set of all complex numbers. Later, throughout our discussion on groups we will see the use of complex numbers under different binary operations [12].
which represents the set of all complex numbers. Later, throughout our discussion on groups we will see the use of complex numbers under different binary operations [12].
The next term we need to define is the identity element.
Definition. The Identity Element
Let ![]() denote an identity element such that
denote an identity element such that ![]() for some set
for some set ![]() . When
. When ![]() is placed in a binary operation with another element
is placed in a binary operation with another element ![]() for which
for which ![]() we have
we have ![]() .
.
It should also be noted that the identity element is not the same under all binary operations. We can conclude that there is only one identity element for each binary operation and thus we can say that each identity element is unique.
Example:
Consider the binary operation ![]() and set
and set ![]() . The identity element is
. The identity element is ![]() . If
. If ![]() is an arbitrary number in
is an arbitrary number in ![]() then
then ![]() .
.
Example:
Consider the binary operation ![]() and the set
and the set ![]() . The identity element is
. The identity element is ![]() . If
. If ![]() is an arbitrary number in
is an arbitrary number in ![]() then
then ![]() .
.
The last term we need to introduce before moving on to groups is the inverse element [12].
Definition. Inverse Element
For a set ![]() and binary operator
and binary operator ![]() , the inverse element
, the inverse element ![]() combined with element
combined with element ![]() produces the following result,
produces the following result, ![]() .
.
Just as identity elements depended on the binary operation, so do inverse elements. Keep this in mind as we look at a few examples.
Example:
Consider the binary operation ![]() on the set
on the set ![]() . The inverse element
. The inverse element ![]() is defined as
is defined as ![]() such that, for
such that, for ![]() it follows that
it follows that ![]() .
.
We know this is correct because we prove in an earlier example that ![]() was the identity element in
was the identity element in ![]() under the binary operation
under the binary operation ![]() .
.
In abstract algebra we want to study the structures that can be created by binary operations. We need to become familiar with how we denote an algebraic structure. If ![]() is a our set and
is a our set and ![]() is our binary operation then we have the algebraic structure
is our binary operation then we have the algebraic structure ![]() . From now on we will use this notation to define our sets.
. From now on we will use this notation to define our sets.
With all the definitions in place for the necessary properties of binary structures we can now introduce groups. We will start with the formal definition of a group.
Definition.
A group ![]() is a set
is a set ![]() , which is closed under a binary operation
, which is closed under a binary operation ![]() and thus satisfies the following axioms:
and thus satisfies the following axioms:
- Associativity of
 :
: 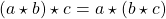 for all
for all 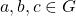 .
. - Identity Element
 : There is an element
: There is an element 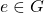 such that for all
such that for all 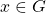 it follows that
it follows that 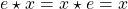 .
. - Inverse Element
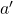 : For each
: For each 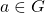 there is identity element
there is identity element 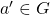 such that
such that 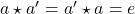
If you notice, we are familiar with every axiom requirement of a group. This makes it very easy to prove or disprove if a set is a group under a specific binary operation; all we need to do is to attempt to satisfy each axiom. If an axiom fails to be satisfied then we can conclude that the set under the binary operation is not a group.
Example:
Let ![]() be a positive integer and let
be a positive integer and let ![]() . Show that
. Show that ![]() is a group [12].
is a group [12].
Let ![]() then
then ![]() and since
and since ![]() then we can conclude that
then we can conclude that ![]() so
so ![]() is closed. Now we can test
is closed. Now we can test ![]() for the three axioms of groups.
for the three axioms of groups.
- Consider
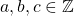 such that
such that 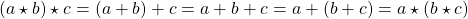 . Thus we can conclude that the binary property + is associative for
. Thus we can conclude that the binary property + is associative for 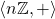 .
. - Since
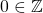 then let
then let 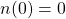 thus
thus 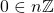 . Since
. Since 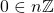 then there is an
then there is an 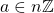 such that
such that 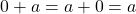 . Therefore we can conclude that 0 is the identity element for the binary operation +.
. Therefore we can conclude that 0 is the identity element for the binary operation +. - Let
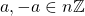 such that
such that 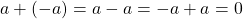 . We have already proven that
. We have already proven that 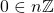 therefore we can conclude
therefore we can conclude 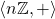 has an inverse element
has an inverse element 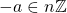 for every
for every 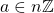 .
.
We can, therefore, conclude that ![]() is a group.
is a group.
Now, we are familiar with the commutative binary operation that was defined earlier. If a group ![]() has a binary operation that is commutative then we call this group an abelian group.
has a binary operation that is commutative then we call this group an abelian group.
Example:
Show that every group ![]() with identity element
with identity element ![]() such that
such that ![]() for all
for all ![]() is abelian [12].
is abelian [12].
Consider ![]() is a group with
is a group with ![]() such that
such that ![]() if we apply
if we apply ![]() to both sides we get
to both sides we get ![]() . Since
. Since ![]() is a group then
is a group then ![]() thus we can simplify
thus we can simplify ![]() to become
to become ![]() .
.
As well, since ![]() is a group, let
is a group, let ![]() then
then ![]() can simplify to
can simplify to ![]() which leads us to conclude that
which leads us to conclude that ![]() equates to
equates to ![]() .
.
Now apply ![]() to both sides to get the following
to both sides to get the following ![]() can be rewritten as
can be rewritten as ![]() . Since
. Since ![]() is a group then let
is a group then let ![]() such that
such that ![]() can be simplified to
can be simplified to ![]() which equates to
which equates to ![]() .
.
Thus we can conclude that ![]() is commutative and thus an abelian group for all
is commutative and thus an abelian group for all ![]() .
.
We have now established groups and abelian groups, we can now look at some of the structural pieces of a group beyond just the axioms. We have discussed topology of real numbers before and in a previous section we even covered the cardinality of sets so this next portion should be familiar to us. Since groups are closed sets it makes perfect sense that they have cardinality [12]. We define group cardinality as the following.
Definition. Order of Groups
If ![]() is a group then the order
is a group then the order ![]() of
of ![]() is the number of elements in
is the number of elements in ![]() .
.
Just as sets have subsets, groups have subgroups and are defined as follows.
Definition. Subgroup
If a subset ![]() of a group
of a group ![]() is closed under the binary operation of
is closed under the binary operation of ![]() and if
and if ![]() with the induced operation from
with the induced operation from ![]() is itself a group; then
is itself a group; then ![]() is a subgroup of
is a subgroup of ![]() . We denote the relationship between subgroup
. We denote the relationship between subgroup ![]() and group
and group ![]() as
as ![]() .
.
In order to confirm that a subset ![]() is a subgroup it too must satisfy a set of axioms.
is a subgroup it too must satisfy a set of axioms.
Theorem: Subgroup Axioms
A subset ![]() of a group
of a group ![]() is a subgroup of
is a subgroup of ![]() if and only if
if and only if
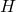 is closed under the binary operation of
is closed under the binary operation of 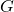 .
.- The identity element
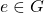 is also in
is also in 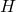 .
. - For all
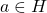 there is an inverse
there is an inverse 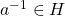 .
.
This is quite straight forward, in the following example we will see how to structure a proof to prove a subset is a subgroup of a group.
Example:
Given the set ![]() of pure imaginary numbers including 0. Determine whether the given subset of the complex numbers is a subgroup of the group
of pure imaginary numbers including 0. Determine whether the given subset of the complex numbers is a subgroup of the group ![]() of complex numbers under addition [12].
of complex numbers under addition [12].
- Let
 , if
, if 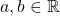 then
then 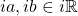 such that
such that 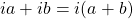 and since
and since 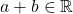 then we can conclude that
then we can conclude that 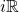 is closed under addition.
is closed under addition. - Let
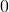 be the identity element of
be the identity element of 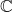 so
so 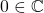 . Then there is
. Then there is 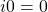 such that
such that 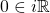 and thus we conclude that the identity element
and thus we conclude that the identity element 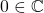 is also in
is also in 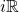 .
. - Let
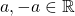 , if
, if 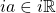 then
then 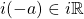 such that
such that
![]()
Therefore we conclude that for each ![]() there is an inverse element
there is an inverse element ![]() .
.
Therefore we can draw the conclusion that ![]() is a subgroup of
is a subgroup of ![]() .
.
Just as sets have proper and improper subsets, groups have proper and improper subgroups. We don’t need to make a grand entrance for these terms but it should be understood that an improper subgroup of group ![]() is a subgroup that contains
is a subgroup that contains ![]() where as a proper subgroup is anything else, it simply cannot contain
where as a proper subgroup is anything else, it simply cannot contain ![]() .
.
There is also a subgroup known as the trivial subgroup. This group contains only the identity element, denoted ![]() . It can also be said that if a group is anything other than just
. It can also be said that if a group is anything other than just ![]() then it is non-trivial.
then it is non-trivial.
Having a strong understanding of how subsets can qualify as subgroups is important for comprehending the following subsection. Keeping in mind the order of groups we move to discuss cyclic subgroups.
21.1 Cyclic Subgroups
Cyclic groups are fascinating to comprehend. We know trivial subgroups are the groups containing only the identity element but this is quite simple and straightforward. Cyclic groups on the other hand are groups that are generated by one element applied with a binary operation or the elements inverse applied with a binary operation [12].
Definition. Cyclic Subgroup
Let ![]() be a group and let
be a group and let ![]() . Then the subgroup
. Then the subgroup ![]() of
of ![]() , which is said to be the smallest subgroup of
, which is said to be the smallest subgroup of ![]() that contains
that contains ![]() , is the cyclic subgroup of
, is the cyclic subgroup of ![]() generated by
generated by ![]() , and denoted by
, and denoted by ![]() .
.
We mentioned before this idea that a cyclic subgroup contains a single element that generates all the terms of the set. We have a formal definition for the generators that will round out the concept of cyclic subgroups [12].
Definition. Cyclic Generators
An element of a group, ![]() generates
generates ![]() and is a generator for
and is a generator for ![]() if
if ![]() . A group
. A group ![]() is cyclic if there is some element
is cyclic if there is some element ![]() that generates
that generates ![]() .
.
We can now see how fascinating cyclic subgroups and groups are because of how unique they are in their structural makeup. In our previous section on set theory, we looked at sets with all integers or all natural numbers. A cyclic subgroup or cyclic group not only needs to satisfy the axioms for subgroups or groups, respectively, but also need to be unique in their makeup.
Example:
The subgroup of ![]() generated by
generated by ![]() . Find the order of the cyclic subgroup of the given group generated by the indicated element.
. Find the order of the cyclic subgroup of the given group generated by the indicated element.
To find the order of the cyclic subgroup we need to find the value for ![]() which satisfies
which satisfies
![]() . If we let
. If we let ![]() then we have the following calculations:
then we have the following calculations:
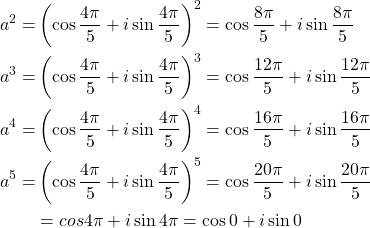
Thus we can conclude that the order of the cyclic subgroup of ![]() generated by
generated by ![]() is 5.
is 5.
It is pretty clear to see that we were able to calculate the order by simply applying the binary operation to the generator until we reached the conclusion of the identity ![]() .
.
This next definition will not really come into use until our discussion of factor groups but because it pertains to cyclic groups we will define it now.
Definition. Greatest Common Divisor
Let ![]() and
and ![]() be two positive integers. The positive generator
be two positive integers. The positive generator ![]() of the cyclic group
of the cyclic group
![]()
under addition is the greatest common divisor, gcd, of ![]() and
and ![]() . We write
. We write ![]() for some integers
for some integers ![]() and
and ![]() .
.
The purpose of introducing the greatest common divisor is because cyclic groups, being generated by a single element with an applied binary operation, means there is some common divisor between two integers under a cyclic group. To make sure we understand how to find the ![]() of a group before we use it in further theorems, let us take a look at an example.
of a group before we use it in further theorems, let us take a look at an example.
Example:
List the elements of the subgroup generated by the subset ![]() of
of ![]()
Let ![]() be a subgroup of
be a subgroup of ![]() generated by
generated by ![]() . Thus, we say
. Thus, we say ![]() is an intersection of all the subgroups of
is an intersection of all the subgroups of ![]() that contain
that contain ![]() and
and ![]() . The divisors of 4 are 1,2,4 and the divisors of 6 are 1,2,3,6. Thus the greatest common divisor is 2 so the subgroup generated by
. The divisors of 4 are 1,2,4 and the divisors of 6 are 1,2,3,6. Thus the greatest common divisor is 2 so the subgroup generated by ![]() of
of ![]() is
is ![]() .
.
We now have a good understanding of greatest common divisors and how to find them so let us continue in our discussion of cyclic groups by covering some of the structural properties of cyclic groups. We begin with acknowledging that every cyclic group is abelian, which have already been defined in our previous discussion on basic groups and subgroups. This leads us to the next formal property of cyclic groups, a subgroup of a cyclic group is cyclic.
The last property may seem a bit confusing as we have been mentioning subgroups and groups almost interchangeably. We began with defining a cyclic subgroup but then moved to introduce cyclic groups from our definition and understanding of generators. If we have a cyclic group then there are cyclic subgroups, as well we have a non-cyclic group there is at least one cyclic subgroup.
Theorem:
Let ![]() be a cyclic group with generator
be a cyclic group with generator ![]() . If the order of
. If the order of ![]() is infinite, then
is infinite, then ![]() is isomorphic to
is isomorphic to ![]() . If
. If ![]() has finite order
has finite order ![]() , then
, then ![]() is isomorphic to
is isomorphic to ![]() .
.
Here we see how important it is to have the knowledge of cyclic groups and order as they are key to describing some of the relations we see in Abstract Algebra. Although we cannot easily draw from these absract ideas to better understand basic algebra we can better understand the structural properties of sets applied with binary operations. In the last theorem we were introduced to the term “isomorphic”. In the next section we will explain isomorphisms and why they are important to abstract algebra.
21.2 Isomorphism
We have been talking about algebraic structures and classifying sets as groups and subgroups. We can now turn our attention to a very important relation classification for binary algebraic structures, Isomorphism. This is a fundamental term learned in Abstract Algebra and involves mapping one set to another, denoted with ![]() . We will look at the formal definition and some examples below to better understand the mapping of binary algebraic structures and how they can qualify as isomorphisms.
. We will look at the formal definition and some examples below to better understand the mapping of binary algebraic structures and how they can qualify as isomorphisms.
Definition.
Let ![]() and
and ![]() be binary algebraic structures. An isomorphism of
be binary algebraic structures. An isomorphism of ![]() with
with ![]() is a one-to-one function
is a one-to-one function ![]() mapping
mapping ![]() onto
onto ![]() such that
such that ![]() for all
for all ![]() .
.
The equation ![]() given in the definition for an isomorphic structure is known as the homomorphism property. The reason we do not call an isomorphic structure a homomorphic structure is because isomorphism is used in place for a homomorphism on a binary structures because the homomorphism property does not prove that
given in the definition for an isomorphic structure is known as the homomorphism property. The reason we do not call an isomorphic structure a homomorphic structure is because isomorphism is used in place for a homomorphism on a binary structures because the homomorphism property does not prove that ![]() is one-to-one, a requirement of an isomorphism. Consider the following example.
is one-to-one, a requirement of an isomorphism. Consider the following example.
Example:
Consider ![]() with
with ![]() where
where ![]() for all
for all ![]() . Determine if the map is an isomorphism or not.
. Determine if the map is an isomorphism or not.
Proof:
- Let
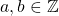 , if
, if 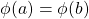 then
then 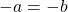 since
since 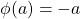 and
and 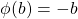 . If we divide both sides by
. If we divide both sides by 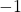 we get
we get 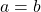 . Thus we can conclude that
. Thus we can conclude that 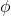 is one-to-one.
is one-to-one. - Consider
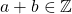 such that
such that
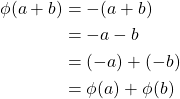
Thus we can conclude that ![]() is onto
is onto ![]() and given (1) we can conclude
and given (1) we can conclude ![]() is bijective.
is bijective.
- Let
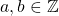 and since the specified binary operation is + we have
and since the specified binary operation is + we have
![]()
We have satisfied the homomorphism property.
Since we have proven ![]() to be bijective and satisfied the homomorphism property we can conclude that
to be bijective and satisfied the homomorphism property we can conclude that ![]() for
for ![]() is an isomorphism of
is an isomorphism of ![]() with
with ![]() .
.
We can note the strategy for proving that ![]() is an isomorphism or not. By the definition of an isomorphism we know that there are 3 axioms that need to be satisfied in order for a map
is an isomorphism or not. By the definition of an isomorphism we know that there are 3 axioms that need to be satisfied in order for a map ![]() to be considered isomorphic. If ever
to be considered isomorphic. If ever ![]() cannot be proven one-to-one, or onto, or satisfy the homomorphism property we can immediately conclude that
cannot be proven one-to-one, or onto, or satisfy the homomorphism property we can immediately conclude that ![]() is not isomorphic. You will have noticed this is the same strategy used in proving groups.
is not isomorphic. You will have noticed this is the same strategy used in proving groups.
Isomorphisms can also be used to describe the relation between subgroups. Let us look at the following example to see this idea proven.
Example:
Let ![]() be an isomorphism of a group
be an isomorphism of a group ![]() with a group
with a group ![]() . If
. If ![]() is a subgroup of
is a subgroup of ![]() , then
, then ![]() is a subgroup of
is a subgroup of ![]() . That is, an isomorphism carries subgroups into subgroups [12].
. That is, an isomorphism carries subgroups into subgroups [12].
First ![]() and since
and since ![]() is a subgroup then
is a subgroup then ![]() such that
such that ![]() where
where ![]() and given that
and given that ![]() then we can conclude that
then we can conclude that ![]() is closed under the operation
is closed under the operation ![]() .
.
Next, since ![]() is a subgroup of
is a subgroup of ![]() then there is the identity element
then there is the identity element ![]() such that
such that ![]() . If
. If ![]() is isomorphic then
is isomorphic then ![]() is the identity element of
is the identity element of ![]() and since
and since ![]() is a subgroup of
is a subgroup of ![]() and
and ![]() then
then ![]() . Thus we conclude that
. Thus we conclude that ![]() is the identity element of
is the identity element of ![]() and
and ![]() .
.
Lastly, Let ![]() then
then ![]() . Since
. Since ![]() is a subgroup of
is a subgroup of ![]() then there is inverse
then there is inverse ![]() such that
such that ![]() . If
. If ![]() is an isomorphism then
is an isomorphism then ![]() thus
thus ![]() . Thus we can conclude that
. Thus we can conclude that ![]() is the inverse element of
is the inverse element of ![]() .
.
Thus we can conclude that ![]() is a subgroup of
is a subgroup of ![]() .
.
Here we can see that being isomorphic can be the key to proving subgroups can lead to other subgroups of other groups. everything we have looked at thus far pertain to the structural properties and axioms of sets with algebra. In the next subsection we continue our study of group structure and relations to other groups.
21.3 Factor Groups
We are familiar with groups, subgroups and orders of groups. Through Abstract Algebra we repeatedly solve for subgroups or are asked to find the order of subgroups and groups. When you continuously relate subgroup orders to group orders we can start to see that the order of a group ![]() is a multiple of the order of a subgroup
is a multiple of the order of a subgroup ![]() of
of ![]() . We can define this as
. We can define this as ![]() (order of
(order of ![]() ) = (order of
) = (order of ![]() ), where
), where ![]() is the coset of
is the coset of ![]() .
.
There are right and left cosets for a subgroup and we can easily define them as the following [12].
Definition.
Let ![]() be a subgroup of a group
be a subgroup of a group ![]() . The subset
. The subset ![]() of
of ![]() is the left coset of
is the left coset of ![]() containing
containing ![]() , while the subset
, while the subset ![]() is the right coset of
is the right coset of ![]() containing
containing ![]() .
.
It can easily be distinguished that the right and left strictly describe the coset’s position affecting the subgroup. It may seem irrelevant to specify the position of the coset but this is not the case as the only subgroup for which the right and left coset partitions are the same is when a group is abelian.
This leads to an interesting theorem for left and right coset relations to subgroups.
Theorem: Lagrange Theorem
Let ![]() be a subgroup of a finite group
be a subgroup of a finite group ![]() . Then the order of
. Then the order of ![]() is a divisor of the order of
is a divisor of the order of ![]() .
.
This theorem solidifies that ![]() as it is defined in our definition of left and right cosets does not change the elements of the subgroup. This theorem exists to steer people away from the idea that
as it is defined in our definition of left and right cosets does not change the elements of the subgroup. This theorem exists to steer people away from the idea that ![]() , itself, contains multiple elements that may effect the order of
, itself, contains multiple elements that may effect the order of ![]() . Now continuing on our discussion of left and right cosets, in the case that a group has not been noted as abelian or has not been proven abelian but for which we need to find the left and right cosets, if we can prove that the left and right cosets will be equal then we only need to find either the left or right cosets. We see this in the following example.
. Now continuing on our discussion of left and right cosets, in the case that a group has not been noted as abelian or has not been proven abelian but for which we need to find the left and right cosets, if we can prove that the left and right cosets will be equal then we only need to find either the left or right cosets. We see this in the following example.
Example:
Find all cosets of the subgroup ![]() of
of ![]() .
.
We use the additive form ![]() for all cosets of
for all cosets of ![]() containing
containing ![]() . Since
. Since ![]() we can say the left and right cosets are equal so we only need to find the left cosets.
we can say the left and right cosets are equal so we only need to find the left cosets.
- Let
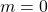 then
then 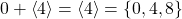 .
. - Let
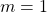 then
then 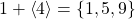 .
. - Let
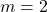 then
then 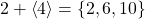 .
. - Let
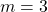 then
then 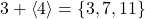 .
. - Let
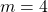 then
then 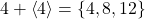 .
.
We do not need to continue this pattern for ![]() or
or ![]() because they result in a set that has already be found. Thus we can conclude that we have found all the cosets of the subgroup
because they result in a set that has already be found. Thus we can conclude that we have found all the cosets of the subgroup ![]() of
of ![]() , listed above.
, listed above.
We could not discuss cyclic groups without introducing the following theorem [12].
Theorem: The Fundamental Theorem of Finitely Generated Abelian Groups
Every finitely generated abelian group ![]() is isomorphic to a direct product of cyclic groups in the form
is isomorphic to a direct product of cyclic groups in the form
![]()
where the ![]() are primes, not necessarily distinct, and the
are primes, not necessarily distinct, and the ![]() are positive integers. The direct product is unique except for the possible rearrangement of the factors; that is, the number of factors
are positive integers. The direct product is unique except for the possible rearrangement of the factors; that is, the number of factors ![]() is unique and the prime powers
is unique and the prime powers ![]() are unique.
are unique.
Let us look at an example that brings together everything we have covered of factor groups so far.
Example:
Find the order of the given element of the direct product ![]() in
in ![]() .
.
Firstly, the divisors of 2 are 1,2 and the divisors of 6 are 1,2,3,6. Therefore the greatest common divisor between ![]() and
and ![]() is
is ![]() . We can find the order by dividing the number of elements in the group 2,6) by the greatest common divisor, which we found to be
. We can find the order by dividing the number of elements in the group 2,6) by the greatest common divisor, which we found to be ![]() . The number of elements in the group
. The number of elements in the group ![]() is
is ![]() , thus we find
, thus we find ![]() . Next, we need to find the greatest common divisor between the value we just found,
. Next, we need to find the greatest common divisor between the value we just found, ![]() , and
, and ![]() since we are given
since we are given ![]() . The divisors of 3 are 1,3 and the divisors of 15 are 1,3,5,15 therefore the
. The divisors of 3 are 1,3 and the divisors of 15 are 1,3,5,15 therefore the ![]() . As we did before, we will divide the number of elements in the group
. As we did before, we will divide the number of elements in the group ![]() by
by ![]() and we find the order to be
and we find the order to be ![]() . Now multiply the orders
. Now multiply the orders ![]() and
and ![]() together,
together, ![]() . Thus we can conclude that the order of
. Thus we can conclude that the order of ![]() in
in ![]() is 15.
is 15.
Here, in this example, we were able to use the greatest common divisor as it relates to the finite elements of the product of two groups, in order to be able to derive the order of the cyclic group.
The next algebraic structure we are going to cover follows a set of axioms just like groups and isomorphisms, which bring together terms and properties we are now already familiar with. This will expand our understanding even further as to how specific properties paired together can define an entire category of sets with a binary operation.
