Primes

Maggie Schildt

30 Primes

There are some numbers that have no proper factors, in other words they are whole numbers greater than one that are not a product of two other whole numbers.

Definition.

Let $p$ be a prime number then there is no $a,b\in \mathbb{Z}$ such that $ab=p$ , in other words the only two whole numbers whose product is prime $p$ is 1 and $p$ such that $1p=p$ .

By this definition for primes we know that any prime number is a number that can only be divided evenly by either itself or 1. Primes are a unique category integers, all other integers are considered composite numbers. It is essential to understand what primes are as they create the foundation for all other integers. As always in mathematics there are different categories for prime numbers. We introduce one below [12].

Definition. Mersenne Primes

Primes of the form $2^{p}-1$ where $p$ is prime are known as Mersenne Primes.

Mersenne primes are unique in that the prime must follow the format $2^{p}-1$ for which $p$ is another unrelated prime. Consider the prime number 3,5,7 which produce Mersenne primes $2^{3}-1=7$ , $2^{5}-1=31$ , and $2^{7}-1=127$ respectively. Continuing on the discussion of prime structures we introduce the Fundamental theorem of arithmetic as it applies to prime numbers.

Theorem: The Fundamental Theorem of Arithmetic

Let $a\in \mathbb{Z}$ and $p$ be some prime in $\mathbb{Z}$ . For any $a>1$ , either $a$ is some prime $p$ or is a product of primes, or can be written as a unique product of prime numbers.

The Fundamental theorem of arithmetic is named so because it is one of the principle theorems surrounding the structure of primes. What this theorem implies is that any integer is either a prime or can be made from primes. This is important because it is a fundamental component of integers. As the study of number theory would suggest we are focusing on the structural components of numbers.

Example:

Consider the integers $72$ , $45$ , and $20$ .

If we look carefully we can write out each integer as follows:

$\begin{equation*} \begin{split} 72&=12 \times 6\\ &=3\times 4\times 3\times 2\\ &=3\times 2\times 2\times 3\times 2\times\\ 45&=5\times 9\\ &=5\times 3\times 3\\ 20&=10\times 2\\ &=5\times 2\times 2 \end{split} \end{equation*}$

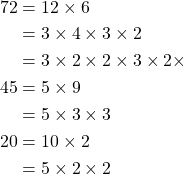
Here our prime numbers in use are $5$ and $3$ .

In this example we can see that if we break down the integers that produce $72$ , $45$ , and $20$ . No matter if the integer is even or odd, they cannot be produced without prime numbers. As well we can see that any combination of primes and composite numbers will produce any other integer.

30 Primes

License

Share This Book